美国杨百翰大学Dan Smalley实验室的研究人员发明了一种用光线投影实体的方法。这种显示技术”能够产生目前全息技术、光场技术无法获得的图像和几何结构，因为它不需要将全息图像投影在固定的物体上，只需要通过空气中看不见的微粒就可以创建三维动态图像（从任何角度观看都可以）。这也让星球大战中的全息影像变得更加触手可及。

研究人员将这种技术命名为“自由空间立体显示（free-space volumetric displays）”，他们也在光阱显示平台上复现了这一技术。他们称这项技术能在空间中创造图像点，这项技术也是最接近流行小说中三维显示的一项技术。虽然这项技术能在自由空间中创建全彩图像，但是仍然局限在一个非常小的规模。

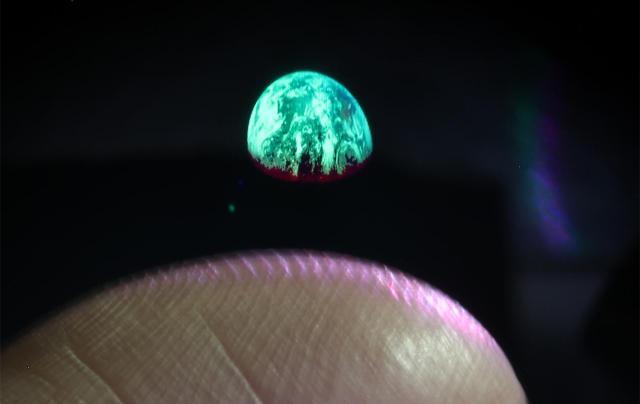
上面图片就展示了利用“自由空间立体显示”技术投影在手指末端的行星图像。

其不仅是“真”三维显示，还拥有惊人的1600DPI（每英寸点数）的高分辨率。

这里展示的光阱显示器只能创建非常小的图像，他们相信以后图像会变得更大。而这些投影的3D图像是利用10微米的图像点通过视觉暂留创造的。

如果真正的全息投影诞生了，就不用仅仅依靠360VR全景来复现场景了，三维立体动态图像将会获得更广泛的应用。

但是在这之前，360VR全景图像依然发挥着不可忽视的作用，艾卓悦为商铺创建全景图像提供一个良好的设备和展示空间。虽说全景和全息仅仅一字之差，但是性质却天差地别，相信3D全息投影的技术开发成功，离它变成消费产品也就不远了。

你们期待3D全息投影产品的诞生吗？有什么脑洞大开的创意？欢迎留言一起讨论吧~

      总编辑圈点

      演示视频中，一只小巧的由光产生的3D蝴蝶，在科学家指尖翩跹。它和我们在星战中看到的很像，但这种技术却和全息完全不一样。你可以在任何角度看到它，包括后面，而全息则不行。它就如同光的3D打印产品，在散射和移动的共同作用下，形成了3D图像。尽管它现在还很微小，也不容易捕捉，但我们欣喜地看到，一个未来派小说中的虚幻场景，已经来到了身边。

（张梦然）