矩阵乘法是机器学习中最基础和计算密集型的操作之一。因此,研究社区在高效逼近矩阵乘法方面已经做了大量工作,比如实现高速矩阵乘法库、设计自定义硬件加速特定矩阵的乘法运算、计算分布式矩阵乘法以及在各种假设下设计高效逼近矩阵乘法(AMM)等。
在 MIT 计算机科学博士生 Davis Blalock 及其导师 John Guttag 教授发表的论文《 Multiplying Matrices Without Multiplying 》中,他们为逼近矩阵乘法任务引入了一种基于学习的算法,结果显示该算法显著优于现有方法。在来自不同领域的数百个矩阵的实验中,这种学习算法的运行速度是精确矩阵乘积的 100 倍,是当前近似方法的 10 倍。这篇论文入选了机器学习顶会 ICML 2021。此外,在一个矩阵提前已知的常见情况下,研究者提出的方法还具有一个有趣的特性——需要的乘加运算(multiply-adds)为零。
这些结果表明,相较于最近重点进行了大量研究与硬件投入的稀疏化、因式分解和 / 或标量量化矩阵乘积而言,研究者所提方法中的核心操作——哈希、求平均值和 byte shuffling 结合可能是更有前途的机器学习构建块。
也有网友表示:「这篇论文为实现更高效的 AI 打开了一扇门。」
对于有网友提到的「该研究在硬件实现方面似乎很有发展前景」,一作本人现身 reddit 并给出了回复:「我们的编码表示是密集矩阵,所以布局和访问模式看上去基本与 GEMM 内核相同,也就意味着可以很容易地使用脉动阵列或修正张量核心来实现。在 x86 上,一般只需要一个 vpshufb-add 指令和一个 4-bit 解包指令就可以了。」
下面来看这篇论文的技术细节和实验结果。
技术细节
具体来说,该研究专注于 AMM 任务,并假设矩阵是高的(tall),并且相对密集,存在于单个机器内存中。在这种设置下,研究者遇到的主要挑战是在给定保真度水平下最小化近似线性运算所需的计算时间。这种设置会很自然地出现在机器学习和数据挖掘中,当一个数据矩阵 A 的行是样本,而一个线性算子 B 希望应用这些样本,B 可以是一个线性分类器、线性回归器,或嵌入矩阵,以及其他可能性。
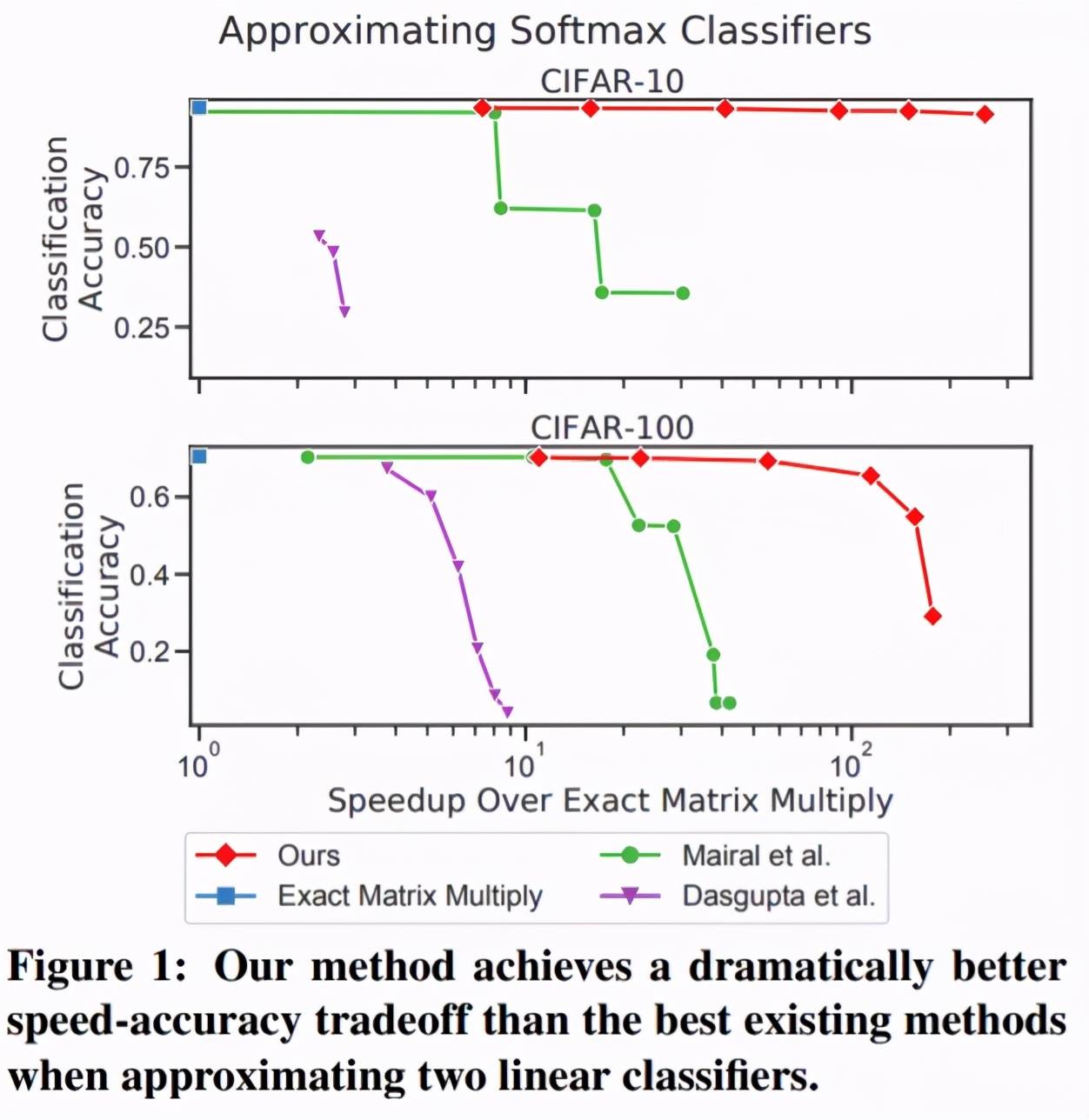
举例来说,考虑一个近似 softmax 分类器的任务,以预测来自神经网络嵌入的图像标签。在这里,A 的行是每个图像的嵌入,B 的列是每个类的权值向量。分类是通过计算乘积 AB 并在结果的每一行中取 argmax 来执行的。图 1 结果表明,在 CIFAR-10 和 CIFAR-100 数据集上,使用该研究的方法及其最佳性能竞争对手的方法近似 AB 的结果。
该研究所用方法与传统方法背离,传统的 AMM 方法构造矩阵 V_A,V_B ∈ R^(D×d), d<<D,如下所示:
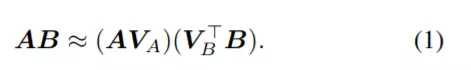
通常,V_A、V_B 是稀疏的,包含某种采样方案,或者具有其他结构,使得这些投影操作比密集矩阵乘法更快。简而言之,这些方法使用线性函数对 A 和 B 进行预处理,并将问题简化为低维空间中的精确矩阵乘法。
该研究提出 MADDNESS 方法 ,该方法采用非线性预处理函数,将问题简化为查表。此外,在 B 提前已知的情况下,即将训练好的线性模型应用于新数据等情况时,MADDNESS 不需要任何乘 - 加运算。该方法与用于相似性搜索的矢量量化方法密切相关。然而,该研究没有使用太多的乘 - 加量化函数,而是引入了一系列不需要乘 - 加的量化函数。
本文的贡献总计如下:
- 一个高效的学习矢量量化函数族,可以在单个 CPU 线程中每秒编码超过 100GB 的数据。
- 一种用于低位宽整数( low-bitwidth integers)的高速求和算法,可避免 upcasting、饱和和溢出。
- 基于这些函数的近似矩阵乘法算法。数百个不同矩阵的实验表明,该算法明显优于现有替代方案。并且还具有理论质量保证。
实验结果
为了评估 MADDNESS 的有效性,研究者用 c++ 和 Python 实现了该算法和其他几个现有算法。评估结果如下。
MADDNESS 到底有多快?
研究者首先分析了 MADDNESS 的原始速度。在图 3 中,他们为各种矢量量化方法计算 g(A)函数的时间,结果表明,MADDNESS 比现有方法快两个数量级,其吞吐量随行的长度而增加。
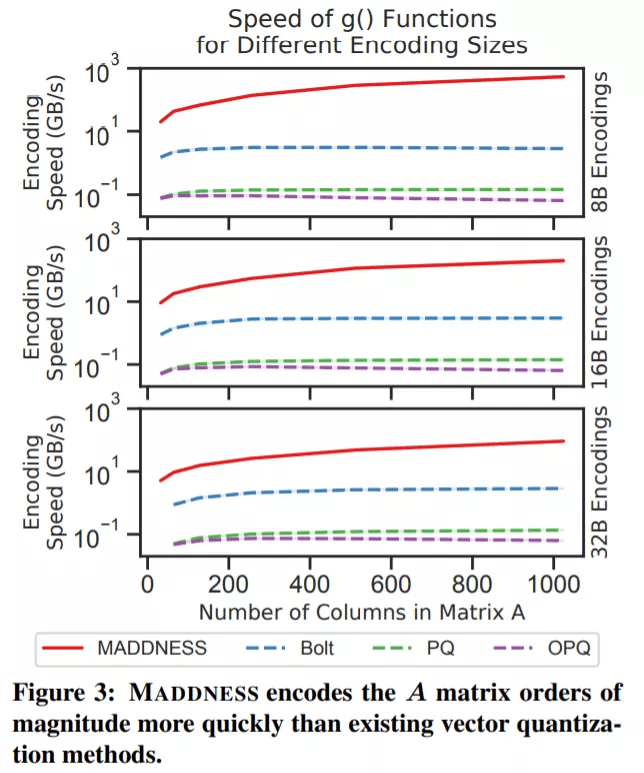
从上图可以看出,Bolt(蓝色虚线)是与 MADDNESS 最接近的竞争对手。研究者还使用与 Bolt 相同的基线分析了聚合函数 f(·,·)的速度。如图 4 所示,他们基于 average 的、matrix-aware 的聚合方法明显快于 Bolt 基于 upcasting 的方法。
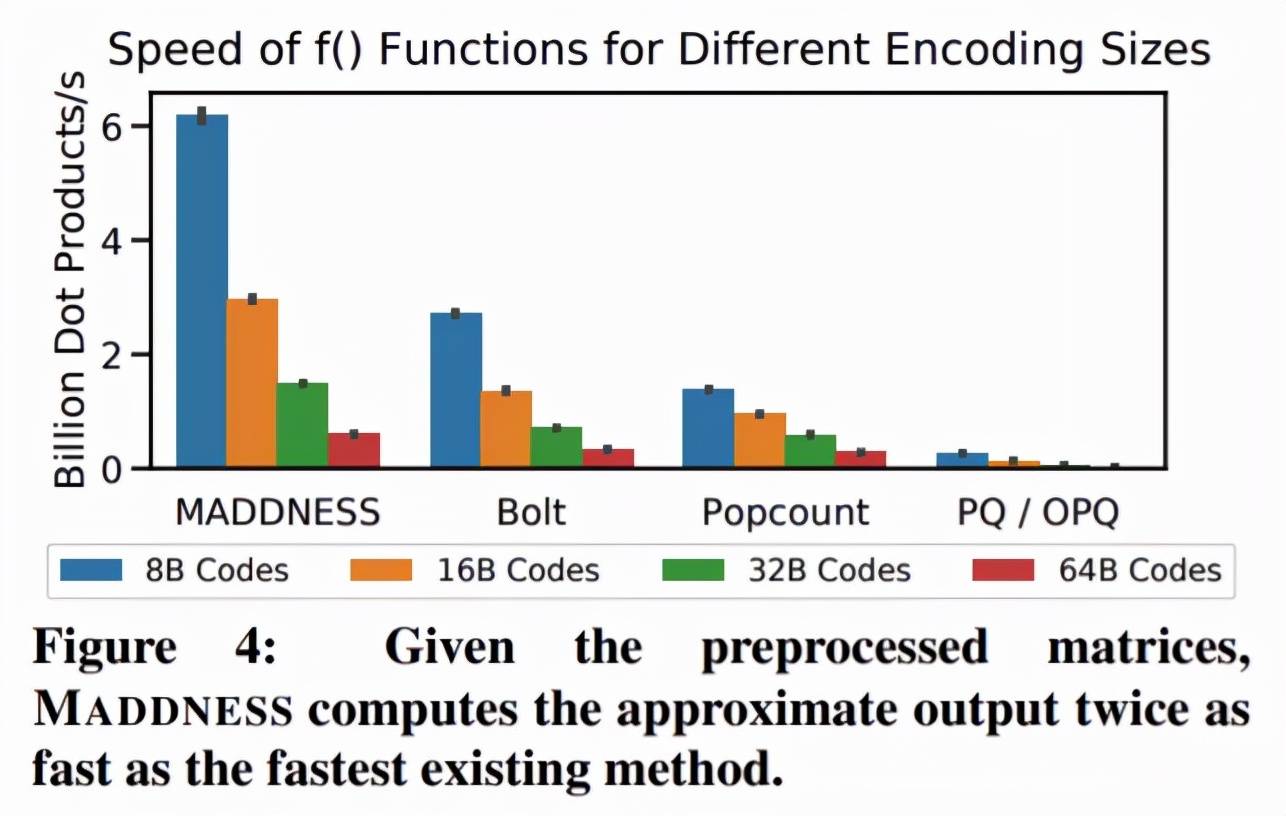
Softmax 分类器
前面说过,研究者在广泛使用的 CIFAR-10 和 CIFAR-100 数据集上近似线性分类器。如图 5 所示,MADDNESS 显著优于所有现有方法,几乎达到了与精确乘法相同的准确率,但比精确乘法快了一个数量级。而且,MADDNESS 是在硬件支持较差的情况下实现了这种性能。
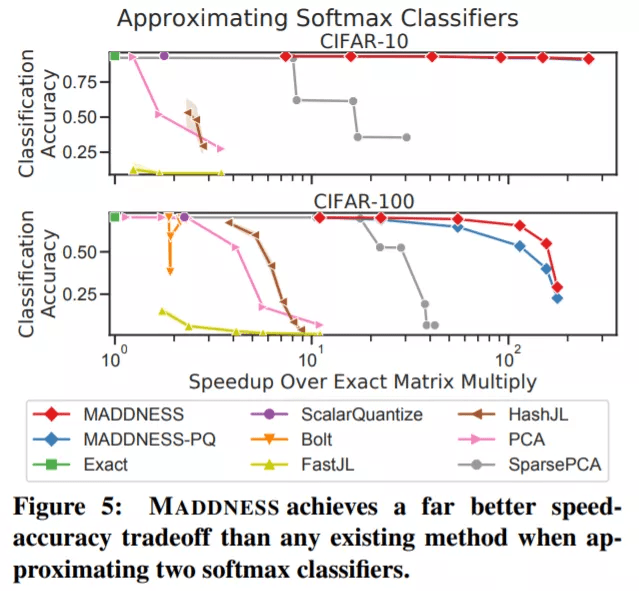
基于 kernel 的分类
为了评估该方法在更大、多样性更强的数据集上的表现,研究者在来自 UCR Time Series Archive 的数据集上训练了 kernel 分类器。结果如下图 6 所示,MADDNESS 在给定准确率的情况下明显快于替代方案。
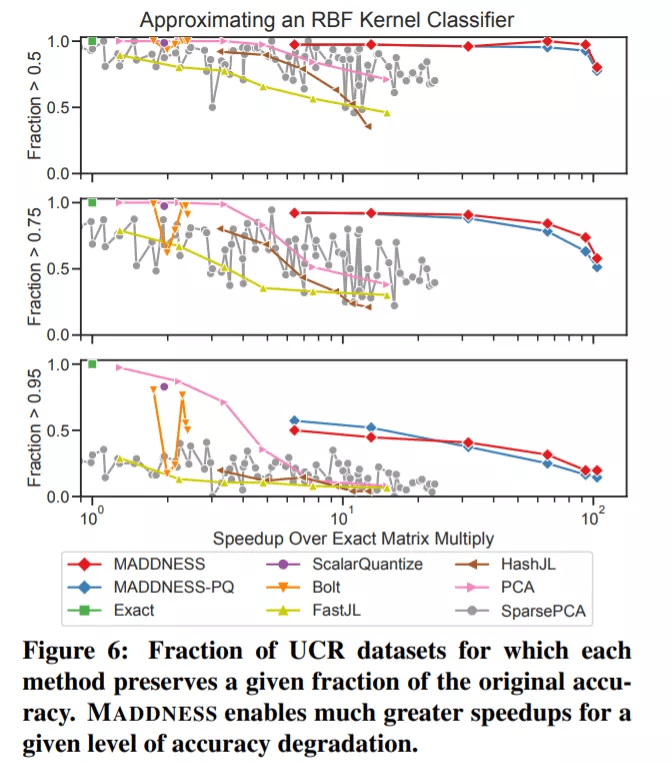
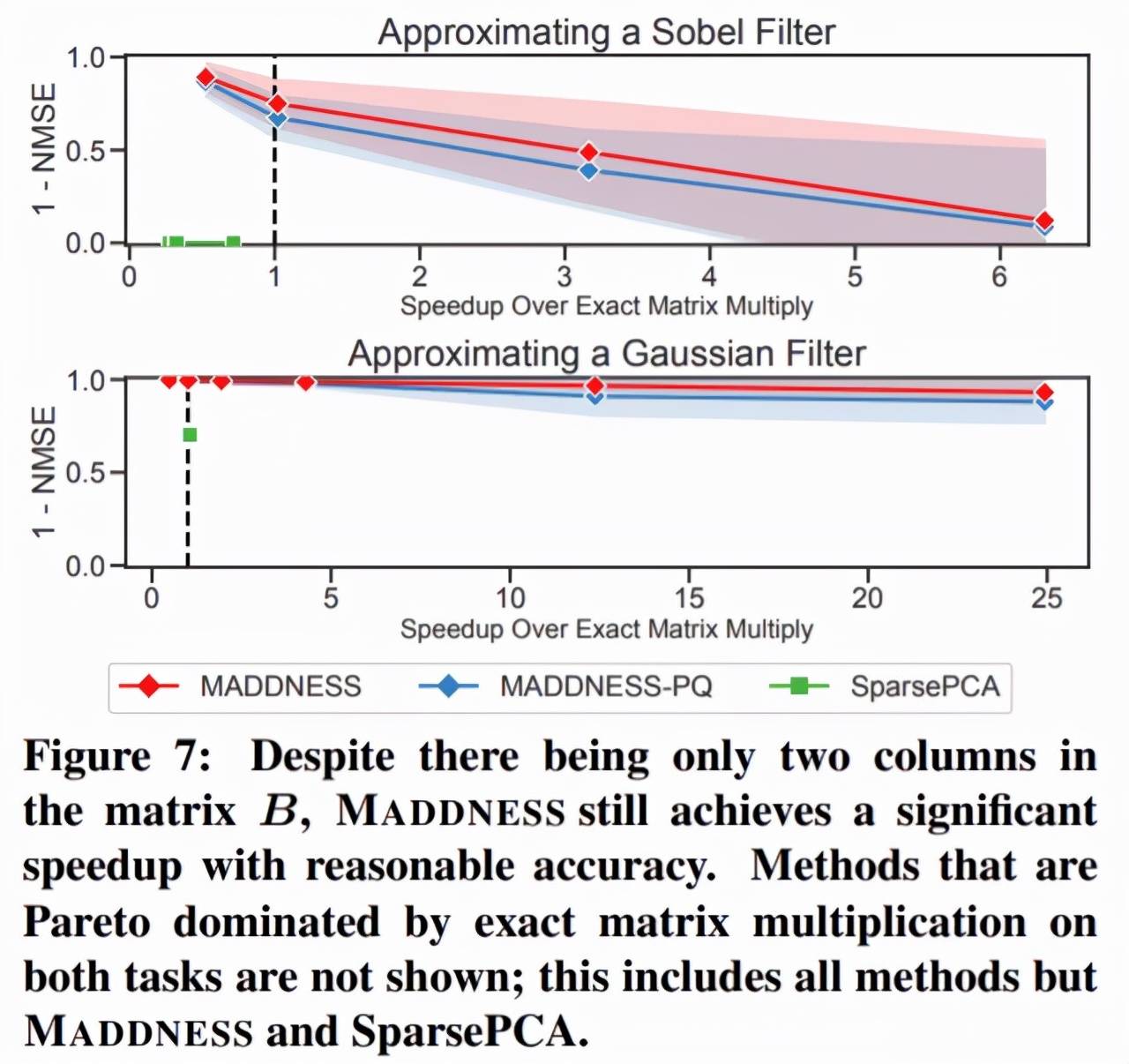
图像滤波
为了测试 MADDNESS 的极限,研究者对将小滤波器应用于图像的各种技术能力进行了基准测试。结果如下图 7 所示,只有 MADDNESS 比精确矩阵乘积更有优势。
作者简介
Davis Blalock

个人主页:https://dblalock.github.io/about/
Davis Blalock 是麻省理工学院的博士生,由 John Guttag 教授指导。他的主要研究方向是设计高性能的机器学习算法,以减少人们在机器学习速度、准确性、隐私和安全性之间的妥协。他于 2014 年获得弗吉尼亚大学学士学位,2016 年获得麻省理工学院硕士学位。他是 Qualcomm Innovation Fellow、NSF Graduate Research Fellow 和 Barry M. Goldwater Scholar。
John Guttag
John Guttag 是麻省理工学院计算机科学与电气工程教授、ACM Fellow。他领导着麻省理工学院计算机科学和人工智能实验室(CSAIL)的临床与应用机器组。该小组负责开发和应用先进的机器学习和计算机视觉技术,以解决各种临床相关问题,目前的研究项目包括预测和减少不良医疗事件,帮助患者匹配治疗方法和治疗者,以及医学成像。
他是《Python 编程导论》一书的作者,其在 MIT 的课程已全部公开,在B站上也可以搜到。

参考链接:https://www.reddit.com/r/MachineLearning/comments/pffoo8/r_multiplying_matrices_without_multiplying

















