我们用一个例子来说明 HTPS 的优势：假设 a 和 b 都是质因子为 7 的自然数，并且 7 也是 a + b 的质因子，如果假设 7^7 可以整除（a + b）^7 - a^7 - b^7，那么请证明 a + b 至少是 19。

假如让人类来证明的话，他们大概率会用到二项式。而 HTPS 使用 Contraposition 方法，大大简化了方程，然后再检查多种不同的情况。

contrapose h₄,

simp only [nat.dvd_iff_mod_eq_zero, nat.add_zero] at *,

norm_num [nat.mod_eq_of_lt, mul_comm, nat.add_mod] at h₄,

如下图为本文模型发现的证明示例，即在 miniF2F 中另一个 IMO 问题的证明：

更接近人类的推理

为了使用计算机编写正式的数学证明过程，数学家最常用的方法是交互式定理证明器（ITP）。下图 1 是交互式定理证明器 Lean 中的一个证明示例：

相应的证明树如下：

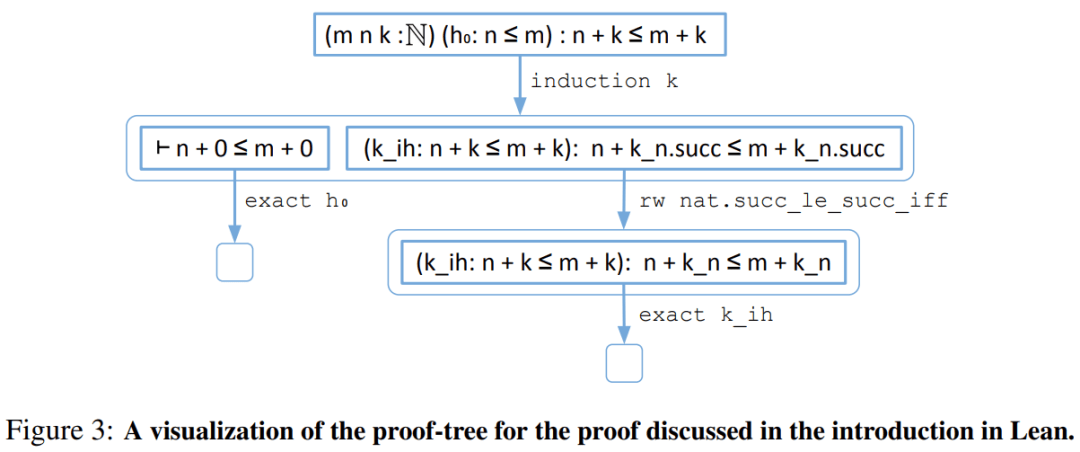
给定一个要自动证明的主要目标 g，证明搜索与学习模型和定理证明环境交互以找到 g 的证明超树。证明搜索从 g 开始逐渐扩展出一个超图。当存在从根到叶子均为空集的超树时，即为证明完成。

以下图 5 证明过程为例，假设策略模型 P_θ 和批评模型 c_θ，以目标为条件，策略模型允许对策略进行抽样，而批评模型估计为该目标找到证明的能力，整个 HTPS 的证明搜索算法以这两个模型为指导。此外，与 MCTS 类似，HTPS 存储访问计数 N（g, t）（在节点 g 处选择策略 t 的次数）和每个策略 t 针对目标 g 的总动作（action）值 W（g, t）。这些统计数据将用于选择阶段。

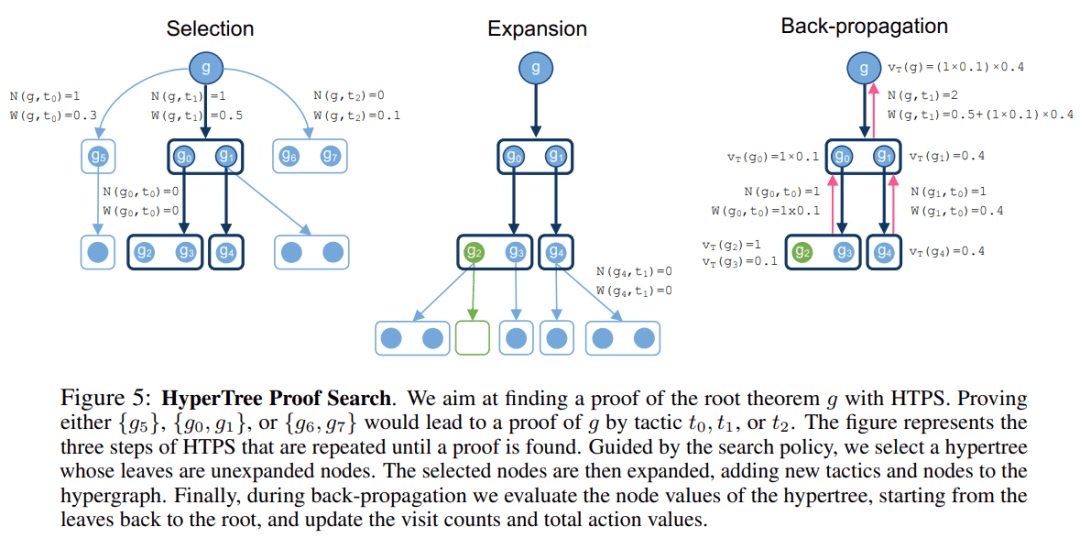
HTPS 算法迭代地重复图 5 描述的选择、扩展、反向传播三个步骤来增长超图，直到找到证明或者超出扩展预算。

Meta 在三个定理证明环境中开发和测试 HTPS：a）Metamath，b）Lean 和 c）Metamath。Metamath 附带一个名为 set.mm 的数据库，其中包含 30k 个人类编写的定理。Lean 附带一个由人类编写的 27k 定理库，称为 Mathlib。最后，由于 Metamath 证明非常难以理解，因而 Meta 开发了自己的环境，称为 Equations，仅限于数学恒等式的证明。

为了模仿人类思维，神经定理证明器需要将特定状态和当前状态（对问题的理解）联系起来。Meta 首先从强化学习开始，该方法与现有的证明助手（proving assistants，例如 Lean）紧密结合。

Meta 将证明的当前状态解释为图中的一个节点，并将每一个新步骤解释为一条边。此外，研究者意识到还需要一种方法来评估证明状态的质量——类似于在棋盘游戏中 AI 需要评估游戏中的特定位置。

受蒙特卡洛树搜索（MCTS）启发，Meta 采用在两个任务之间进行循环：在给定证明状态下使用的合理参数的先验估计；给定一定数量的参数后的证明结果。

HTPS 是标准 MCTS 方法的变体，在该方法中，为了探索图，Meta 利用关于图的先验知识来选择一组叶进行展开，然后通过备份修正来改进初始知识。图是逐步探索的，关于图结构的知识随着迭代得到细化。

实验

每个实验都在单一环境（例如 Lean、Metamath 或 Equations）上运行，并将模型与 GPT-f 进行比较，它代表了 Metamath 和 Lean 的最新技术。

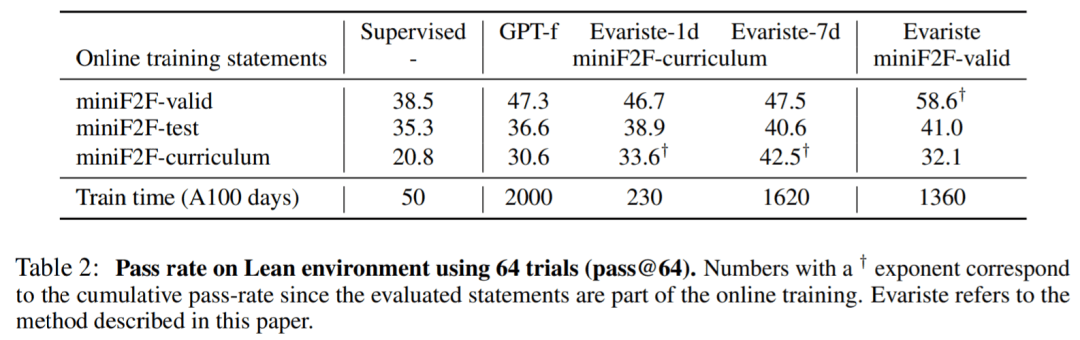
在 Lean 中，该研究在 A100 GPU 上使用 32 个训练器和 200 个证明器进行实验。经过 1 天的训练（即（200 + 32）A100 天的计算），miniF2F 中的每个状态（statement）平均被采样 250 次，在 327 个状态中已经有 110 个被解决。本文的模型在 miniF2F-test 中优于 GPT-f，具有大约 10 倍的训练时间加速。

在 Metamath 中，该研究在 V100 GPU 上训练模型，使用 128 个训练器和 256 个证明器，表 3 报告了监督模型和在线训练模型的结果。

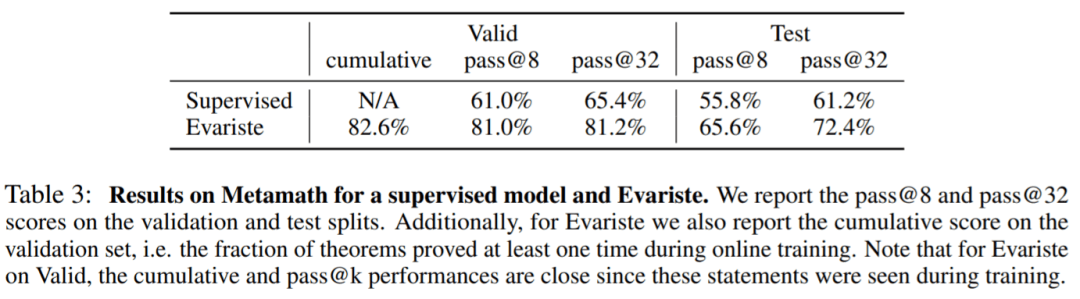
在 Equations 中，该研究使用 32 个训练器和 64 个证明器进行实验，在这种环境下，模型很容易学习随机生成器的训练分布，并解决所有综合生成的问题。

参考链接：https://ai.facebook.com/blog/ai-math-theorem-proving/