它使得该理论看起来比实际上更难。然而,如果你熟悉复数,那么你已经遇到了一个例子,那就是那些于模为1的复数,
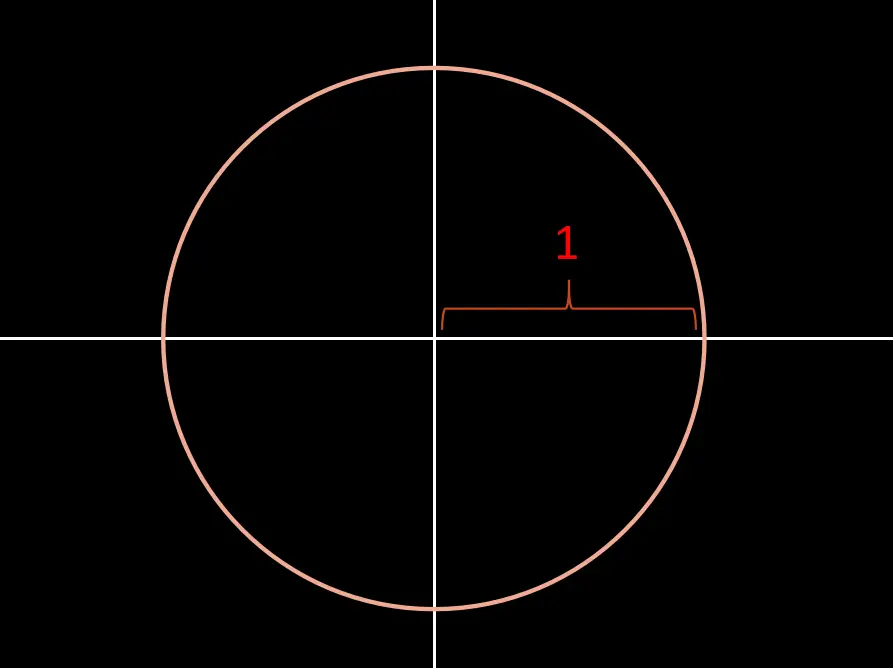
你的本能反应可能是将这些数字视为 e^(i θ)。
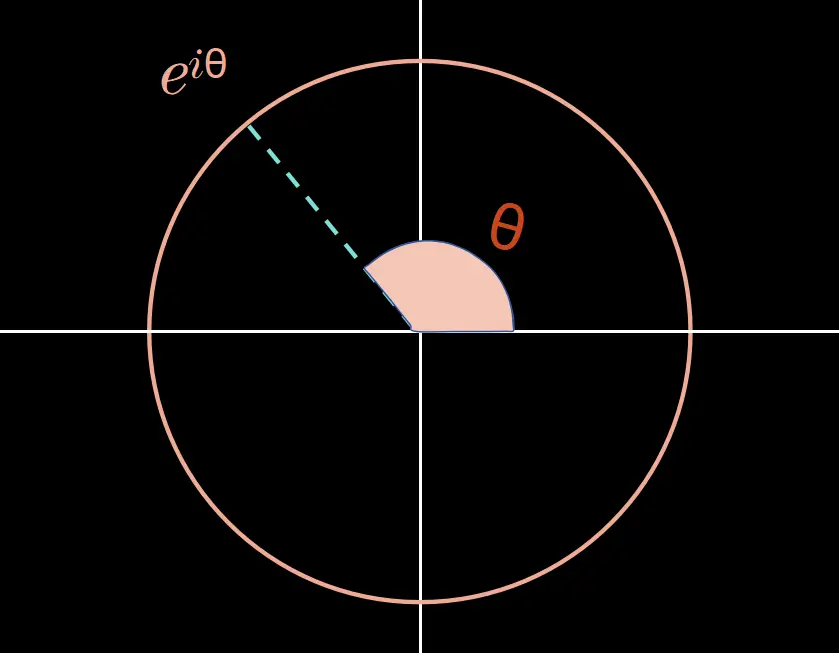
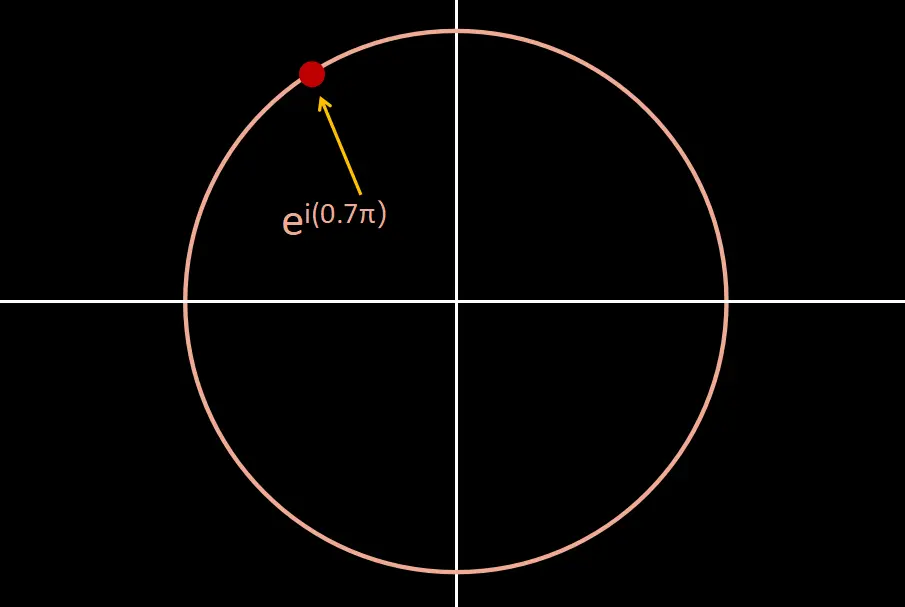
但如果你更深入地思考,实际上是在这个复数圆上施加了一个坐标系统,例如,我们可以说这一点是 e^(i * 0.7π),
这个圆是所谓的李群(Lie group)的一个例子,将在稍后解释,但一般来说,它可以是更高维的,更难以可视化的。李理论的精髓是,即使在这些复杂的情况下,也要尽量施加一个坐标系统,使其更容易处理。
让我们稍微详细地阐述李理论,从李群开始。李群同时是两个东西,它是一个群,但也是一个流形。
李群-群
首先让我们了解一下什么是群,因为它是一个更容易的概念。
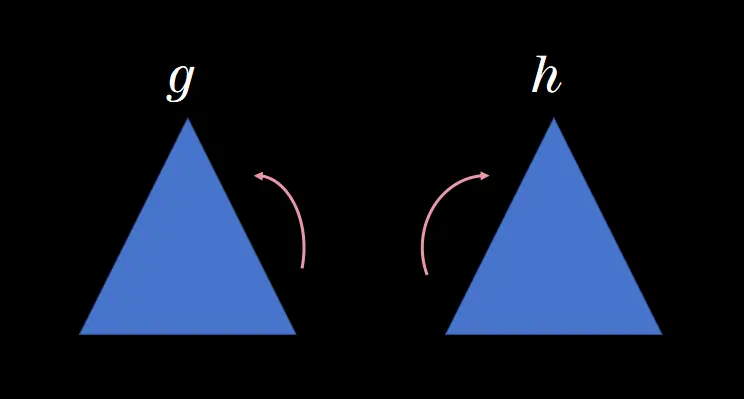
群基本上是一组满足某些属性的对象,使它们看起来具有对称性。我们期望对称性满足的第一个属性是封闭性。以正三角形的对称性G为例,我们将 h 表示为沿斜轴的反射对称性,g 表示为沿垂直轴的另一个反射对称性,那么将 g · h 定义为函数组合,即首先做 h,然后做 g。事实证明,g 和 h 组合是一个旋转。结果不重要-重要的是结果仍然是一个对称性,因此它仍然在 G 中。
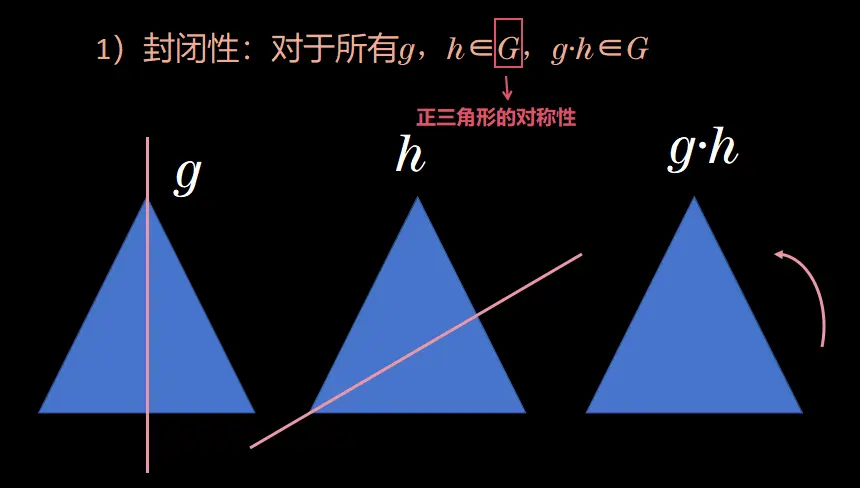
但为了使这个公理成立,我们需要对每对 g 和 h 都证明这一点。你可以逐个验证这个情况,但根据定义,对称性是任何保持对象不变的变换。所以如果 g 和 h 是对称的,它们保持对象不变,那么当然,先做 h 然后做 g 也会保持对象不变,因此也是一个对称性。
对称性还遵循一些其他属性,如“结合律”:
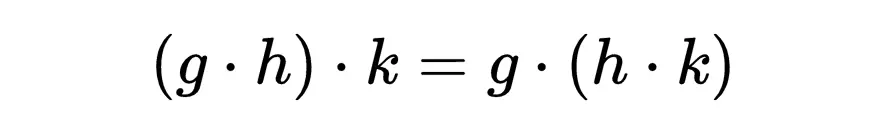
如存在一个恒等元:
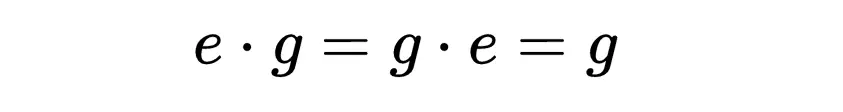
最后,对称性都有一个逆:
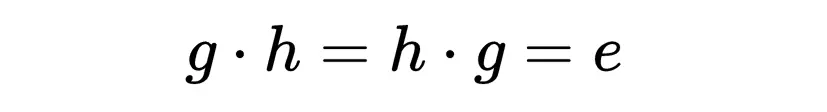
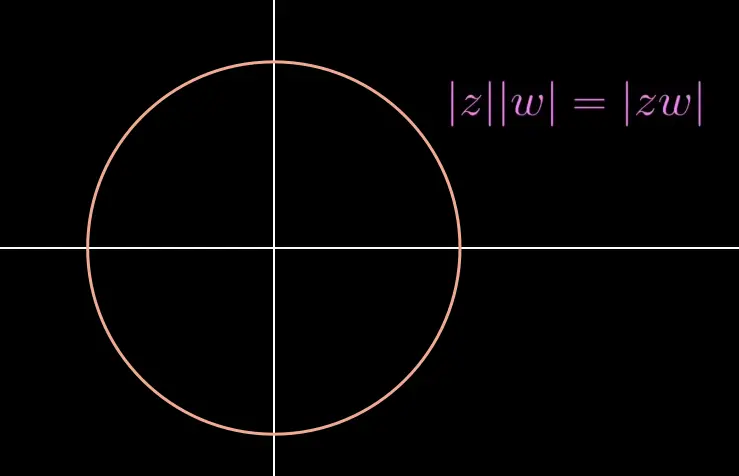
如果一组对象满足这4个条件,它就构成一个群。一个对象的对称性自然地形成一个群。如果给定一组数字或矩阵,比如一开始的复数单位圆,检查该集合是否满足这些属性是很有必要的。在这种情况下,你只需要使用模数相乘,甚至不需要用欧拉公式,

当然,不仅仅是这个圆形成了一个群。旋转矩阵的集合,正交或酉矩阵都是群,
如果你对群不太熟悉,我强烈建议你对这些集合的群公理进行补习。你所需要的只是转置、伴随和行列式的一些其他属性,

总之,群只是李理论的一部分。李群也是流形,那么什么是流形呢?让我们通过一个例子来理解:复数的圆。
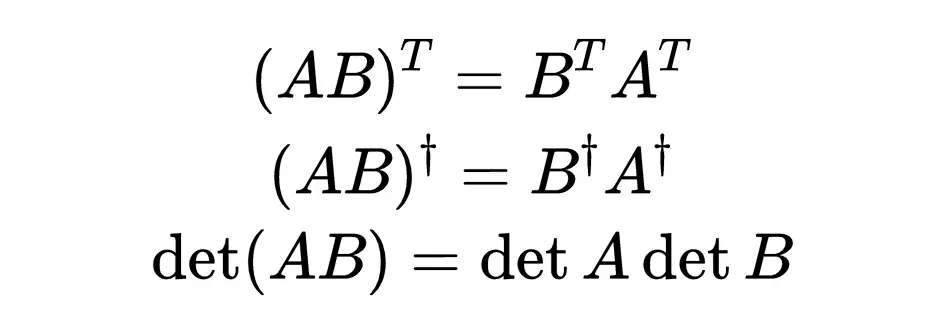
这个圆是流形,意思是在它上面的每一点,其邻域基本上看起来像一条线,只是变形了。让我们放大这一点的邻域。
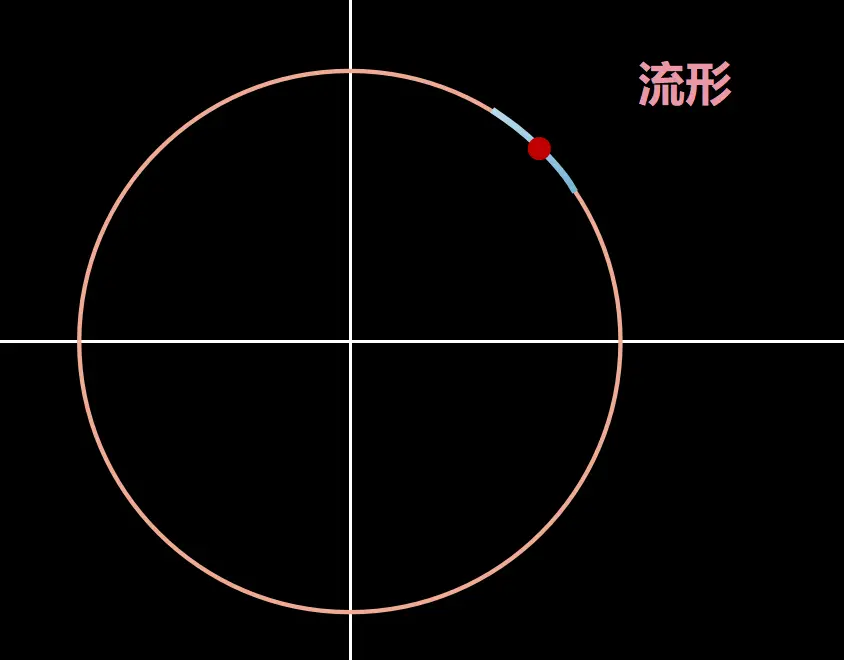
在圆的情况下,这是一个弧,可以平滑地变形为直线。
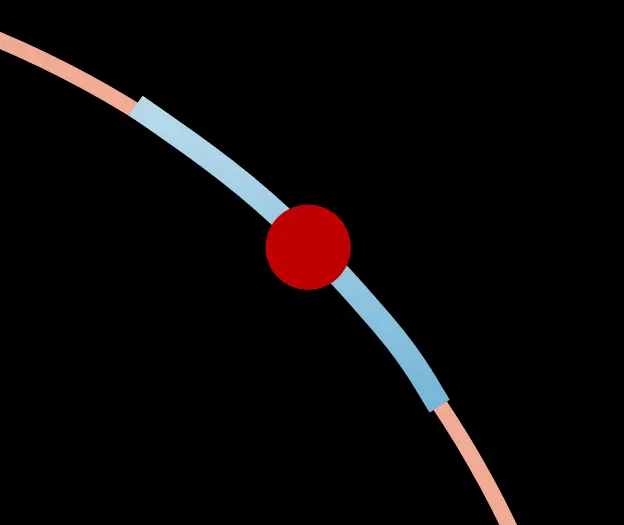
但同样重要的是,这条线也可以平滑地变回弧。这种双向变形就是我所说的“看起来像一条线”。当然,不仅仅是圆上的这一特定点。每个点都有这样的属性,即邻域看起来像一条线。这就是我们称圆为一维流形(1-dimensional manifold)的原因。
但是还有更高维的流形,道理是一样的。