关键词:降维打击;高斯积分;矩阵行列式;谐振子;生成函数
AbstractDimension is an important concept in physics learning and research. In dealing with complicated physical problems, dimensionality reduction methods are often used to simplify the problem, so as to analyze and solve the simplified problem in a low dimensional space. However, when faced with specific physical problems, sometimes increasing the dimensions of the system can make the problem become more intuitive and simpler. This paper takes several specific physical problems as examples such as Gaussian integral, determinant calculation, normalizing the eigenstates of the harmonic oscillator in quantum mechanics, and generating functions of special functions, to demonstrate how to effectively solve the difficulties encountered in low dimensional teaching by improving the dimensions of the system. The purpose of this paper is to emphasize the significance of the concept of “dimension reduced strategy” in physics teaching, and cultivate students divergent thinking abilities.
Key wordsdimension reduced strategy; Gaussian integral; determinant of a matrix; harmonic oscillator; generating function
科幻作家刘慈欣的代表作《三体》一书中,“降维打击”是指外星人将太阳系由三维空间降至二维空间的一种攻击方式。《三体》小说和与之相应的影视作品让“降维打击”这一名词被大家所熟知。这一概念也被人们在生活中使用,表明碾压式的优势。在教学过程中,如果能将具体问题与这种时髦且大家耳熟能详的概念结合,势必能引起学生的兴趣与共振,助力课堂教学。
分析力学比牛顿力学优越的地方之一是引入了抽象的广义坐标的概念,并与系统自由度相对应。实际是一种抽象维度的概念。在物理学中,有很多问题实例涉及维度的概念,由于有些老师在授课中只是具体问题具体分析,同时学生局限于对知识深度的认知,学生未能理解这一类问题的联系或对这类问题形成比较清晰的认识。本文的目的就是通过具体实例凝练出物理学中“降维打击”这一概念,培养学生的发散思维能力,同时在物理学教育同行中起到抛砖引玉的作用。
一般而言,在处理复杂物理问题时,为简化问题,人们都是把高维问题向低维转化,即降维,使得问题能得到解决,例如物理学中的质点近似、抓主要矛盾忽略次要矛盾等思想。但对有些具体问题时,处理方式却恰好相反,是将问题向高维度转化从而使低维问题得解。虽然听上去有些奇怪,但逻辑上是完全可行的,高维比低维包含更多的信息,有可能将在低维上看不清或解决不了的问题给出答案。这个操作实际是升维,但升维的目的是解决低维的问题。针对上面提及的两种改变维度的做法,笔者认为,“降维打击”这一概念都是适用的。以此为契机,本文将以物理学中常见的几个问题:高斯积分、两个矩阵乘积的行列式等于两个矩阵行列式的乘积、量子力学中一维谐振子波函数的归一化、物理学中常用的特殊函数或多项式的生成函数,展示在同维度的情况下难以解决的问题,可以通过变换一种思维方式,将问题向高维度转化从而使问题能得以解决。在物理学教学中明确提出“降维打击”这一概念,给学生种下发散思维的种子,以期提高学生的创新、思辨等能力。
1 高斯积分
在文献[1]中,作者对物理学中常用的高斯及类高斯型积分进行了详述。作者也正是在文献[1]中开始提及在当前维度下如果解决不了问题时,可以发散性的将问题向高维转化的这种想法。此为本文中强调的物理学中“降维打击”这一概念的萌芽。
物理学中非常重要的高斯积分为
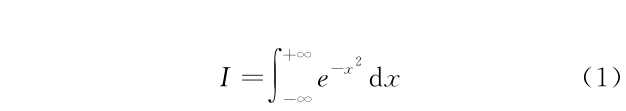
高斯积分的问题是式(1)无法利用牛顿莱布尼兹公式求出原函数对积分进行计算。当然可以选择如 Mathematica 软件对式(1)进行积分给出结果。另外也可以选择通过构造的方法来完成解析积分。在教学训练过程中,我们推荐后者。先计算式(1)平方的积分,这样就可以将式(1)中的一维积分转换为二维积分,从而得以求解。具体过程如下
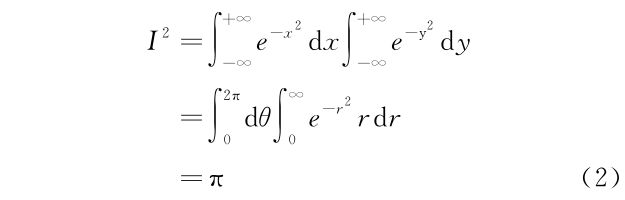
式(2)的过程是将二维笛卡尔坐标中的积分变为极坐标下积分。对式(2)中 r2 进行变量代换,立刻得到一个可以解析计算的指数函数积分。因此
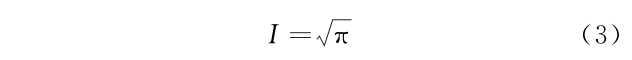
整个计算过程的关键是将高斯积分转化成二维积分,即对问题进行升维,借助高维的优势(此具体问题是能解析积分),完成对低维问题的求解。
高斯积分仅仅是积分类问题中的一个特例,更典型的是利用留数定理去计算一维实函数积分,这一过程是将一维积分转化成二维复平面空间中的积分。
2 两个矩阵乘积的行列式等于两个矩阵行列式的乘积
矩阵在物理学与数学问题中均被广泛地应用。矩阵非常重要的性质之一是两个矩阵乘积的行列式等于两个矩阵行列式的乘积,即
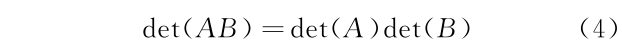
作为矩阵这一性质的特例,在量子力学的矩阵表示中,如果存在两个力学量算符彼此对易,则这两个力学量算符具有共同的本征函数系,这两个力学量的矩阵表示能同时对角化[2,3]。在他们的本征表象中,两个力学量的矩阵表示是对角化的,完全满足式(4)。作为对式(4)的一般性证明,线性代数书上是通过构造更高维度的分块矩阵,使矩阵A,B分别是对角线上的分块矩阵[4]。此证明为线性代数书中的标准过程,在此我们不再重复。我们强调的是一般性证明中运用的“降维打击”的思维方式。
3 一维谐振子波函数的归一化
一维谐振子是量子力学中少数几个可以精确求解的量子力学系统之一,是量子力学教学中必讲的重点内容[2,3]。在本科量子力学教学过程中,对于一维谐振子波函数的归一化是值得讨论的。一维谐振子波函数为
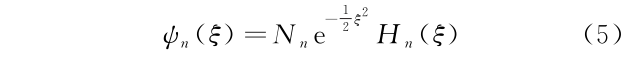
其中,Nn 为需要计算的归一化常数,Hn(ξ)为厄米多项式[5-7]。按照波函数的概率解释,波函数的归一化条件给出
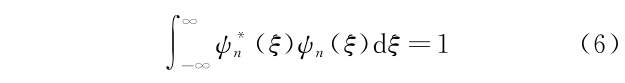
将波函数式(5)代入式(6),为计算归一化常数,必然需要计算积分
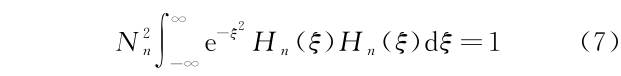
由于厄米多项式是随 n 变化的,显然,对于每一个具体的 n 值去计算相应的归一化常数是不可取的。如何计算归一化常数 Nn 的通用表达式呢?不同的教科书给出的方案可能不一样,但均利用了厄米多项式的生成函数
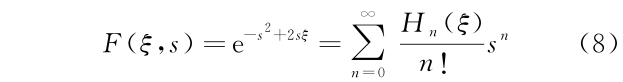
方案之一是构造积分[8]
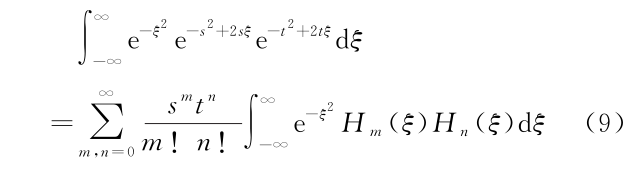
式(9)左边的积分可以利用高斯积分解析计算[1],然后进行泰勒展开,右边的表达式可以利用一维谐振子不同本征值的波函数的正交性将两重求和变为一重求和[2,3],对比左右两边的表达式,可得
对比式(7)与式(10),即得一维谐振子本征波函数的归一化系数的通用表达式。回顾整个过程,非常关键的一步是引入厄米多项式的生成函数式(8)。但生成函数 F(ξ,s)的自变量比厄米多项式 Hn(ξ)的自变量多 1,从一个自变量代表一个维度的角度,此过程即为典型的“降维打击”。同时这个例子也代表了一类问题,即在计算特殊函数或多项式的某些通式时,需要用到“降维打击”的思想。
4 物理学中常用的特殊函数的生成函数
物理学中经常会用到一些特殊函数或多项式,比如上一节中的厄米多项式,勒让德多项式等。在上一节中讨论的厄密多项式的生成函数并不是孤例,而是物理学中常用的这些特殊函数或多项式均存在生成函数[9]。下面写出几个实例:
1)伯努利多项式Image的生成函数为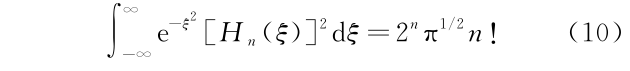
对比式(7)与式(10),即得一维谐振子本征波函数的归一化系数的通用表达式。回顾整个过程,非常关键的一步是引入厄米多项式的生成函数式(8)。但生成函数 F(ξ,s)的自变量比厄米多项式 Hn(ξ)的自变量多 1,从一个自变量代表一个维度的角度,此过程即为典型的“降维打击”。同时这个例子也代表了一类问题,即在计算特殊函数或多项式的某些通式时,需要用到“降维打击”的思想。
4 物理学中常用的特殊函数的生成函数
物理学中经常会用到一些特殊函数或多项式,比如上一节中的厄米多项式,勒让德多项式等。在上一节中讨论的厄密多项式的生成函数并不是孤例,而是物理学中常用的这些特殊函数或多项式均存在生成函数[9]。下面写出几个实例:
1)伯努利多项式Image的生成函数为
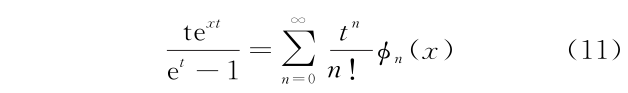
2)欧勒多项式 En(x)的生成函数为
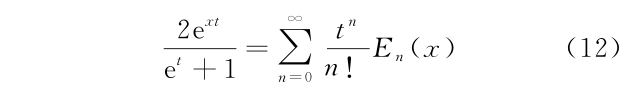
3)贝塞尔函数的生成函数为
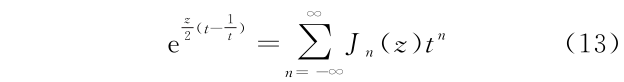
其他的特殊函数或多项式的生成函数就不在此罗列了。可以看出,特殊函数或多项式的生成函数的共性是自变量的个数比特殊函数或多项式的自变量多 1。毋庸置疑的是在涉及特殊函数或多项式的计算过程中,其生成函数会频繁使用,即“降维打击”思想的运用。
5 结语
在处理具体物理问题时,有时候需要“变多为少”,对系统进行降维;而有的时候则需要“变少为多”,对系统进行升维。那么什么时候该“降”,什么时候该“升”呢?降维的意义和应用场景在当前物理教材中已描述得很详细,这里不再赘述。以文中所举的几个例子而言,笔者认为以下几种情况下可以考虑升维:(1)当在低维空间中进行数学分析遇到困难时,如高斯积分;(2)当系统的行为和特征在低维空间中看不清楚时,如矩阵行列式性质的一般性证明;(3)当需要写出系统不同状态下的通项公式时,如波函数的归一化系数和特殊函数的生成函数。当然,在处理具体物理问题的时候,如何升维以及升维多少又是另外两个非常关键的问题,其解决方案依赖于对物理问题的深刻认识,有时也依靠直觉和运气。
本文通过讨论物理学中对维度改变求解问题的现象,明确地将“降维打击”这一概念引入物理学教学过程中,给学生种下发散思维的种子,以期提高学生的创新、思辨等能力,同时在物理学教育同行中起到抛砖引玉的作用,助力课堂教学。

















