据Crafoord Prize克拉福德奖官网近日消息，克莱尔·瓦赞（Claire Voisin，1962 -），法国朱西厄数学研究所（Institut de Mathématiques de Jussieu）的研究员，获得2024年克拉福德数学奖（Crafoord Prize in Mathematics），以表彰其在复几何和代数几何学领域的杰出贡献，包括霍奇理论、代数闭链（algebraic cycle）和超凯勒几何（hyperkähler geometry）等方面。代数几何涉及可以描述为代数方程解的几何形状和结构。与学校学习的基础几何不同，这些形状通常无法形象化，代数几何已发展成为现代数学理论要求最高的领域之一。

瓦赞是首位获得Crafoord克拉福德数学奖的女数学家。

图源：Patrick Imbert

Claire Voisin（克莱尔·瓦赞）在这一领域通过反例和针对一些最著名的未解决问题的积极结果，做出了重要且备受赞誉的贡献。Kodaira小平邦彦问题就是这样一个例子，该问题涉及可以用方程描述的更高维度的几何形状。

在瓦赞的整个职业生涯中，她也是千年七大难题之一霍奇猜想的首席研究员。最近，她开发了一种惊人的方法来确定几何形状是否有理的，这意味着它们是最简单的形状之一。她还在超凯勒几何（hyperkähler geometry）领域处于引领地位。

关于获奖者

Claire Voisin（克莱尔·瓦赞） 是法国国家科学研究中心（CNRS）的高级研究员（特级），在巴黎索邦大学朱西厄数学研究所工作。她于 1962 年 3 月 4 日出生于 Saint-Leu-la-Fôret，并于 1986 年在巴黎奥赛大学获得博士学位。

瓦赞的荣誉包括美国数学会AMS Satter奖（2007年）、克莱研究奖（2008年）、邵逸夫奖（2017年）和欧洲联合国教科文组织奖（2019年）。她是伦巴第研究所、林琴学院、美国国家科学院、皇家学会和艺术与科学学院的外籍成员；德意志自然科学学院、法兰西科学院、欧洲科学院的成员，以及伦敦数学学会的名誉成员。

历史克拉福德数学奖得主一览

其中不乏众多菲尔兹奖、沃尔夫奖、阿贝尔奖得主：

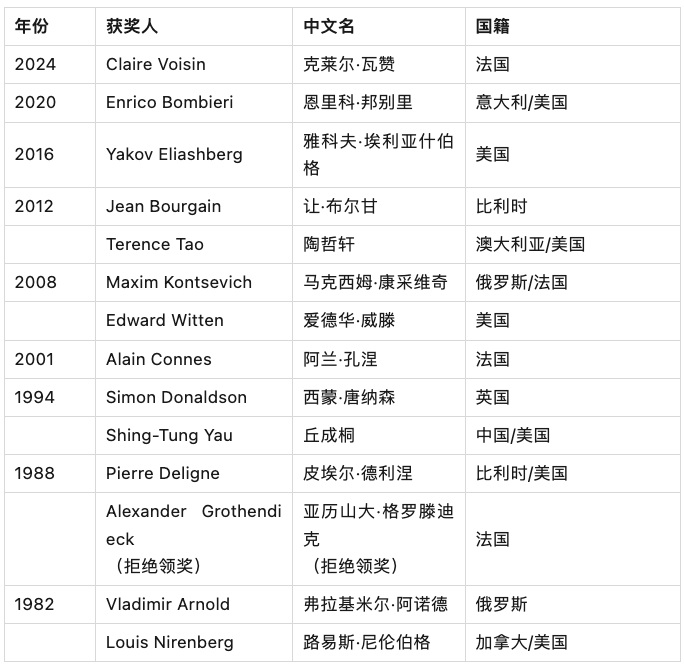
历届克拉福德数学奖获奖原因一览

2020，Enrico Bombieri 恩里科·邦别里

在数学的所有主要领域，特别是数论、分析和代数几何学方面作出了杰出而有影响力的贡献。当他发表第一部数论著作时，年仅16岁，他还是素数分布黎曼假设的领先专家。邦别里还为解决Bernstein伯恩斯坦的问题做出了贡献。这是Plateau普拉托问题的变体，涉及如何用数学方法描述当铁丝框浸入肥皂溶液时形成的肥皂膜的形状。

2016，Yakov Eliashberg 雅科夫·埃利亚什伯格

切触拓扑和辛拓扑的发展，以及对刚性和柔性现象的开创性发现。他进一步发展了他在接触几何中使用的技术，接触几何是辛几何的孪生理论。辛几何处理的是二维、四维或其他偶数维度的空间，而接触理论则描述的是奇数维度的空间。这两种理论都与现代物理学的当前发展密切相关，例如弦理论和量子场论。

2012，Jean Bourgain 让·布尔甘，Terence Tao 陶哲轩

在调和分析、偏微分方程、遍历理论、数论、组合学、泛函分析和理论计算机科学等领域的杰出和开创性工作

2008，Maxim Kontsevich 马克西姆·康采维奇，Edward Witten 爱德华·威滕

来自现代理论物理学对数学的贡献。其结果对于物理学和自然基本规律的研究具有相当大的价值。弦理论是为所有自然力制定理论的雄心勃勃的尝试，根据弦理论，构成宇宙的最小粒子是振动弦。该理论预测了额外维度的存在，并且需要非常先进的数学。获奖者解决了与弦理论相关的几个重要数学问题，并为其进一步发展铺平了道路。

2001，Alain Connes 阿兰·孔涅

算子代数理论，非交换几何学的创始人。

算子代数

20 世纪 30 年代初，匈牙利裔美国数学家约翰·冯·诺依曼开始发展一种称为希尔伯特空间的算子代数理论。他受到量子力学发展的启发，这些代数在量子力学中发挥了核心作用。冯·诺依曼界定了此类代数的一种特殊类型，数学家现在将其称为“冯·诺依曼代数”，以及形成此类代数的特殊类型的构建块，称为因子。冯·诺依曼与 F. J. Murray 一起将这些代数大致分为三类：I、II 和 III。冯·诺依曼后来转向其他兴趣，直到1966年至1971年期间才恢复发展，并构建了许多不同的III型因子。1972 年，Alain Connes开始涉足这一领域。虽然已经完成了大量的准备工作，但在接下来的十年中，孔涅通过解决该领域大多数未解决的问题，彻底改变了这一局面。为此，他于 1983 年荣获菲尔兹奖。

通过进一步发展这一理论，孔涅很快进入了新的、未曾涉足的领域。一个全新的数学领域开始形成，即非交换几何。

非交换几何

从笛卡尔开始发展起来的几何学是基于坐标系中点的概念。几何性质反映在函数的代数性质中，其中空间中的点代表变量。以这种方式构造的代数通常是可交换的，这意味着运算的结果与其执行的顺序无关。一个例子是普通的乘法：a · b = b · a。

但在算子代数的研究中，经常会遇到非交换性质。矩阵乘法是通常不可交换的一个例子：A·B 不等于 B·A。Alain Connes的想法是，使用这样一个不可交换的代数作为基础，将其视为虚构的“非交换”空间。这样的空间需要一种与我们习惯的经典几何不同的、更抽象的概念设置。例如，点的概念在非交换几何中是没有意义的。

Alain Connes的工作还提供了可用于理论物理学处理的强大新方法。重整化理论以及量子和粒子物理的标准模型。他还证明，这些新的数学工具可用于理解和进攻zeta 函数的黎曼假设，该假设被认为是数学中最著名的开放问题。

1994，Simon Donaldson 西蒙·唐纳森，Shing-Tung Yau 丘成桐

Simon Donaldson 西蒙·唐纳森

应用瞬子（instanton）对四维几何进行的基础研究，特别是他发现了新的微分不变量。现代几何主要分为两个方向：考虑距离的微分几何和只关心形状的拓扑。渐渐地，人们已经清楚地认识到，在拓扑学中，一方面是五维或更高维度的几何，另一方面是低维几何。在五六十年代，人们对五维及更高维度的拓扑进行了研究，今天可以说已经很好地理解了。至于低维，从一维到四维，它们都有自己的特点。一维和二维由于其显而易见性而相对简单。三维几何虽然要复杂得多，但其行为与低维几何（尤其是二维几何）非常相似。四维几何似乎是一种临界情况。它与较低维度有根本的不同，而用于较高维度的方法则不起作用。

对五维或更高维度的研究表明，在拓扑学中，有理由考虑允许改变几何对象的形式的程度。连续性是当允许最剧烈的可能变化时使用的概念，可微性是当仅接受光滑变化时使用的概念。对这些维度上这种区别的认识是五六十年代取得的成就的一部分，而在一个、两个和三个维度上可能看不到这种区别。

Shing-Tung Yau 丘成桐

微分几何中的非线性技术。由于丘成桐过去几十年的工作，几何中基本偏微分方程的作用和理解在数学领域发生了巨大的变化和扩展。他的工作对拓扑学、代数几何、表示论、广义相对论以及微分几何和偏微分方程等数学和物理学领域产生了影响。丘成桐是中国传奇数学家陈省身的学生，并曾就读于伯克利大学。作为一名老师，他的想法非常慷慨，他有很多学生，也与很多数学家合作。

1988，Pierre Deligne 皮埃尔·德利涅，Alexander Grothendieck 亚历山大·格罗滕迪克（拒绝领奖）

表彰他们在代数几何方面的基础研究，特别是引入了étale上同性（格罗滕迪克）及其在数学各个领域的应用（格罗滕迪克和德利涅），包括韦伊猜想的证明。获奖者因其在纯数学方面的研究而受到表彰，但相关成果例如：已与纠错码的构造结合使用，例如用来与卫星通信。

代数几何是数学最古老的部分之一，其最原始的形式是关于多个变量的多项式方程解的结构。这个问题既有连续的方面（例如复数中的解），也有离散的方面（例如整数中的解），并且数百年来数学家一直梦想着统一这两种方法，以便得到例如数论中的一般证明方法。但直到最近几十年，这个梦想才得以实现（尽管还有很多事情要做）。与此相关的一个重要推动力是法裔美国数学家安德烈·韦伊（André Weil，生于 1906 年）于 1948 年提出的一些猜想（“韦伊猜想”），特别是当 p 变大时，多项式方程以素数 p 为模的解的数量。这些猜想被Grothendieck和Pierre Deligne彻底证明。与 étale 的概念相关，同调性在他们研究这个概念及其应用的过程中发挥了重要作用。格罗滕迪克和德利涅彻底改变了代数几何。代数几何的后来发展（Faltings 关于费马大定理的工作、Mori 关于代数簇模型的工作以及获奖者和其他人的工作）以非常令人信服的方式证明了这些思想的巨大潜力和力量。

1982，Vladimir Arnold 弗拉基米尔·阿诺德，Louis Nirenberg 路易斯·尼伦伯格

非线性偏微分方程。现代分析完全基于牛顿描述行星绕太阳运动的思想。他将物体的位置、速度和作用力相互联系起来，然后引入了第一个微分方程。这些自然方程是非线性的，因此不能通过显式数学计算来很好地分析，并且许多自然问题仍然悬而未决。借助现代计算机，我们可以做出详细的预测，但行星运动稳定性等问题仍未解决。阿诺德对此类问题做出了非常重要的贡献，并在理解天体运动方面迈出了一大步。在后来的论文中，他处理了映射奇点的一般问题。这些与理解突变理论概念下已知的数学复杂发展的新努力有关。

牛顿的思想被用来描述物理和几何中的许多不同系统，这些系统可能同时取决于多个变量。这些方程被称为偏微分方程，最有趣的是非线性方程。尼伦伯格已经处理了大量此类性质的问题。作为几何学的一个例子，我们可以提到寻找具有给定曲率的表面的问题，以及粘胶流体方程的物理研究以及关于自由流线的存在的问题。尼伦伯格的工作涉及各种问题，对该领域的发展具有基本的重要性。

关于克拉福德奖Crafoord Prize

克拉福德奖由瑞典皇家科学院和克拉福德基金会在瑞典隆德共同颁发。瑞典皇家科学院负责决定获奖者。该奖旨在促进数学和天文学、地球科学、生物科学（特别是生态学）以及多发性关节炎（例如类风湿性关节炎，霍尔格晚年深受多发性关节炎的困扰）等领域的国际基础研究。安娜-格蕾塔和霍尔格·克拉福德基金会成立于1980年，首次颁发该奖项是在1982年。

据瑞典皇家科学院称，“选择这些学科是为了补充诺贝尔奖颁发的学科”。 每年只颁发一个奖项，按照轮流方案——天文学和数学；然后是地球科学；然后是生物科学。只有当特别委员会认为该领域已取得实质性进展时，才会颁发多发性关节炎领域的克拉福德奖。 克拉福德奖的获得者每年一月中旬公布；在四月或五月的克拉福德日，该奖项由瑞典国王颁发，瑞典国王也在 12 月的颁奖典礼上颁发了诺贝尔奖。该奖项在地球科学领域，因其声望而被比作诺贝尔奖。

今年的数学奖获得者将获得600万瑞典克朗奖金。该奖项将在2024年5月13日至16日的隆德和斯德哥尔摩的克拉福德日颁发。瑞典皇家科学院成立于1739年，是一个独立的组织，其总体目标是促进科学并加强其在社会中的影响力。

 参考资料

https://www.crafoordprize.se/news/this-years-crafoord-laureates-can-see-inside-stars-and-describe-geometric-shapes/

https://www.crafoordprize.se/mathematics-astronomy/

http://www.ams.org/news?news_id=7292

https://en.wikipedia.org/wiki/Crafoord_Prize

https://www.kva.se/en/news/this-years-crafoord-laureates-can-see-inside-stars-and-describe-geometric-shapes/