文章来源：

SIAM REVIEW（最新影响因子为：10.2，中科院Q1，JCR Q1）

文章题目：

What Are Higher-Order Networks?
文章地址：

https://epubs.siam.org/doi/abs/10.1137/21M1414024

摘要：使用图语言对复杂系统和数据进行基于网络的建模已成为一系列不同学科的重要主题。可以说，这种基于图的视角的成功源于图的相对简单性：图仅由一组顶点和一组边组成，描述了这些顶点对之间的关系。这种简单的组合结构使图成为可解释的和灵活的建模工具。然而，图作为系统模型的简单性最近在众多文献中得到了仔细研究。具体来说，人们从各种不同的角度认为需要高阶网络，这超出了图封装的成对关系建模范式。在这篇文章中，作者盘点了这些最新进展。其目标是阐明（i）什么是高阶网络，（ii）为什么这些是有趣的研究对象，以及（iii）如何在应用中使用它们。

1 引言

近几十年来，人们对网络和网络动力学系统的兴趣激增，网络和网络动力学系统由互连的实体组成，以理解各种复杂的系统。范围从生物系统（例如基因调控网络）到基础设施系统（例如交通网络）。

网络一词通常指的是图，它是由顶点（或节点）和边（或链接）组成的组合结构。在这个抽象模型中，节点表示系统中的实体，边表示哪些实体交互。将系统表示为图有助于深入了解系统的结构和动态特征：图属性可用于确定重要节点，揭示系统的模块化结构，或者——如果每个节点都是一个动态单元——阐明集体网络动态，例如同步。这些想法已扩展到加权图、符号图、有向图以及具有多个边或节点类型的图（例如多层图或多重图）。然而，任何基于图的方法的局限性在于，所有关系根据定义都是二元或成对关系，因为图中的边是成对关系。例如，在网络动力学中，二元相互作用通常反映在运动方程中，因为两个给定节点之间的相互作用独立于网络中的任何其他节点。

然而，在许多现实世界的系统中，网络交互和关系是非二元的，并且涉及两个以上节点的联合非线性交互。例如，在社会经济系统中，基于群体的互动很常见，活动通常在多个代理（例如买方、卖方、经纪人）之间联合协调。生化系统中的反应通常涉及两种以上的物质（A+B  C+D），或者两种试剂可能仅在存在酶的情况下相互作用。三个或更多节点之间非线性相互作用的重要性在社会科学中也一直存在争议。例如，结构平衡理论意味着社交网络中的三元关系将根据口语规则“朋友的朋友是我的朋友”和“我敌人的敌人是我的朋友”演变。最近对大型在线社交网络的分析证实这些网络确实非常平衡[。同样，同伴压力、联盟和联盟的形成以及经纪活动都是常见社会现象的例子，这些现象确实涉及多人而不是两人的相互交织的活动。还有人认为，联合相互作用对于了解多个相互作用物种的竞争模式至关重要。

为了充分捕获任何此类网络的属性，至关重要的是超越仅捕获二元关系的图，并阐明多元网络交互的影响。多元相互作用和关系在文献中以各种名称进行了讨论，包括超二元、非成对、高阶或单纯。下面，作者将具有这种相互作用的网络统称为高阶网络。但高阶网络到底是什么？它们如何用数学方式表示？有哪些工具可用于分析它们？

术语差异背后的原因之一是高阶网络出现在不同研究领域的不同背景下，这些领域通常具有不同的动机、研究问题和数学工具。本文的主要目的是提供关于高阶网络及其数学表示的综合视角，并回顾这个非常活跃的研究领域的最新进展，重点关注潜在的问题和数学工具。因此，该文补充了最近的其他调查，包括以物理为中心的观点，其中包含广泛的参考文献，对不同高阶模型和依赖性建模之间关系的讨论，以及对信号的调查高阶网络上的处理。具体来说，将在三种情况下讨论高阶网络，它们在其中找到了特定的应用：

数据的拓扑和几何（第 3 节）：高阶网络如何帮助理解数据集的“形状”？

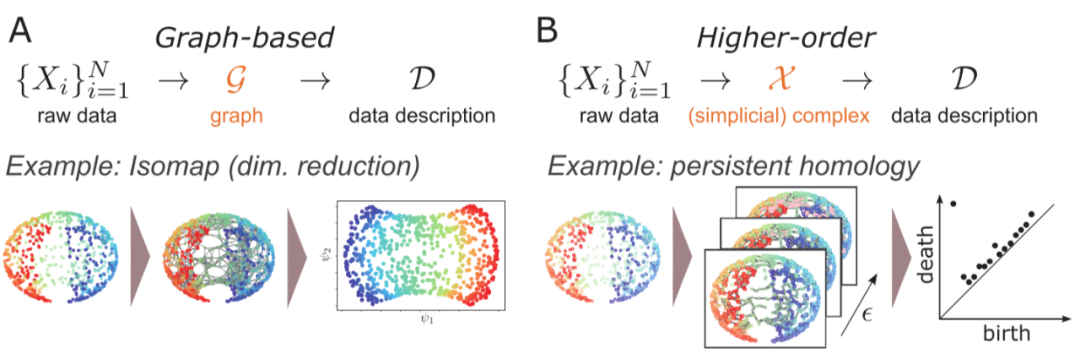
图1. 用于描述数据几何和拓扑的高阶网络

分析和建模关系数据（第 4 节）：如何对高阶关系进行统计建模以及使用此类统计模型的优点是什么？

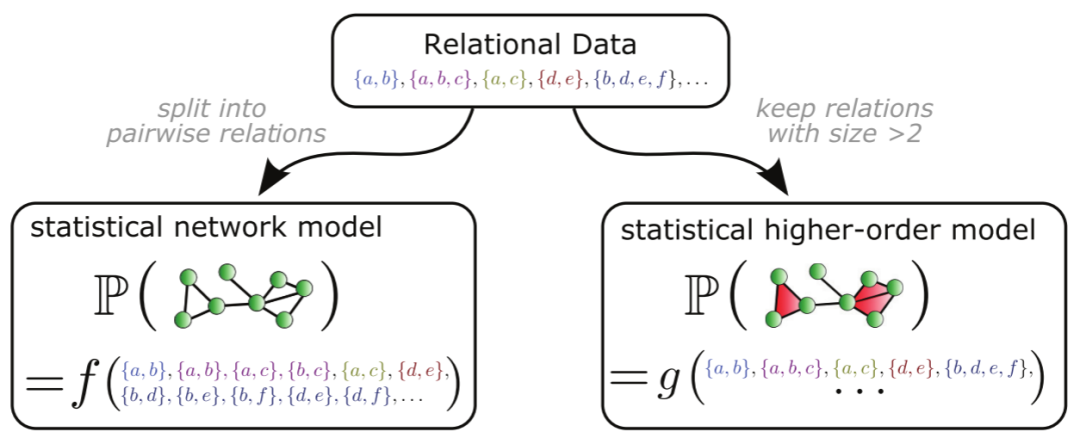
图2. 用于描述关系数据的高阶网络

高阶网络动力学系统（第 5 节）：高阶相互作用如何影响耦合动力学单元的集体动力学？

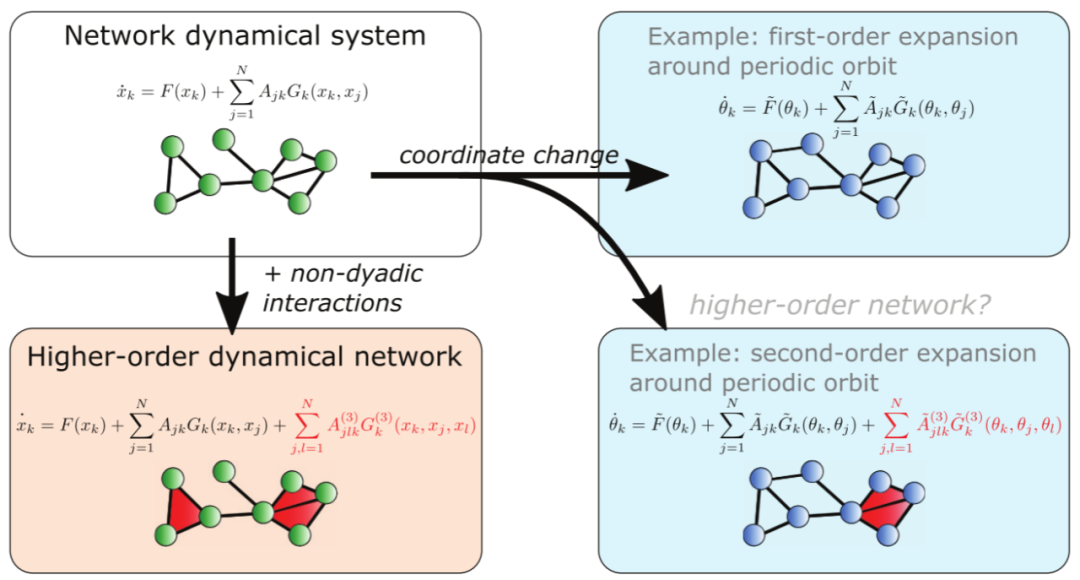
图3. 用于描述动力学单元之间耦合的高阶网络

2 图、超图和单纯复形的简要回顾

超图和单纯复形是可以编码高阶相互作用的数学对象。本节简要地介绍了这些对象的定义。

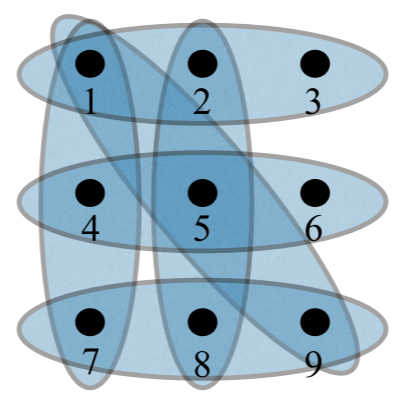
图4. 具有9个顶点和6条边的3-均匀超图

3 高阶网络数据的几何和拓扑

拓扑数据分析（TDA）的中心思想是通过拓扑对象（例如单纯复形）来描述经验观察到的数据（例如点云）。然后，拓扑对象的属性产生一种描述数据的方法。欧拉特征  就是这种性质的一个例子，它以适当的方式给出了大小的度量。类似地，我们将在下一节中描述的同源性提供了一种测量单纯复形属性的方法，例如分量和环的数量。事实上，同调性与欧拉特征密切相关，但提供了对单纯复形拓扑的更详细描述。在下文中，首先关注同源性作为单纯复形的重要拓扑性质，然后再讨论如何使用这些概念来描述数据的高阶结构。

4 使用高阶网络模型理解关系数据

本节描述如何使用（高阶）网络来研究关系数据。在开始更广泛的讨论之前，第4.1小节中强调与迄今为止讨论的高阶模型观点的差异，然后在第4.2小节中对高阶数据的数学含义进行更详细的讨论。在4.3节中讨论基于单纯复形和超图的此类数据的各种概率模型，并在4.4 节中指出几个应用场景。

5 具有高阶交互的网络动力学系统

网络动力学系统描述了相互作用的动力节点的联合演化。节点之间的耦合可以导致有趣的集体网络动力学，例如同步，其中节点一致发展。一个关键问题是网络相互作用——网络结构以及耦合的功能形式——如何塑造这种集体动态。虽然图传统上用于编码网络结构，但我们专注于更通用的“高阶”方法来捕获耦合结构。当然，这会产生诸如以下问题：哪些高阶结构适合网络动力学系统？高阶相互作用如何塑造动力学？在这里，本文关注网络动力学系统，其中节点/顶点是动态单元，尽管最近也讨论了具有动态（超）边的（高阶）网络。

当然，网络动力学系统可以产生数据（例如，通过从轨迹采样），可以应用前面几节中概述的方法。然而，本文将采用更通用的动力学系统方法来阐明相互作用的动力学系统的一般属性。

6 讨论

用于建模和分析高阶网络的各种工具的开发为我们批判性思考和区分我们在不同应用中使用的工具类型带来了新的机会。通常情况下，当数据采用矩阵形式时，该矩阵被解释为图的邻接矩阵或加权邻接矩阵。在许多情况下，这样的解释是合理的，并且会在应用领域带来令人兴奋的新见解。例如，图（例如连接组或相互作用组）是成对关系数据的自然数学结构。但其他时候，图解释是出于必要而使用的——没有分析高阶结构的工具，因此投影到图集上是执行有趣分析的少数方法之一。然而，这种方法的代价是失去了高阶关系和结构，以及一些意义。例如，多篇论文对将协作网络分析为图与超图进行了比较和对比，每一篇文章都说明了将协作网络视为超图时可以获得的新见解。拥有用于高阶网络的工具（例如本评论中讨论的工具）使此类分析成为可能，而且重要的是，它使我们在分析数据时更加意识到我们所做的选择。在建模和分析方面，新工具的开发给我们带来了以下问题：在做出建模决策时，我们如何考虑所做的权衡？我们如何平衡可解释性和便利性？而且，对于具有定量思维的人来说，最重要的是，有没有办法开发一个指导框架来帮助回答这些问题？

虽然经常单独研究（并由不同的社区），但这里讨论的高阶网络的三个方面是相互关联的。一个例子是神经科学中的结构函数关系：神经细胞的结构网络及其连接的特性如何与网络动力学系统的动力学特性相关？一方面，人们可以根据自己的能力分析连接的结构特征：是否是针对小规模网络（例如口胃神经节或秀丽隐杆线虫）明确提取它，还是使用技术例如大规模的扩散张量成像，这些数据是从（高阶）网络角度进行分析的。当然，这些神经系统会产生非加性高阶效应发挥作用的动态（见 5.3.3 小节）。这些动力学最终决定神经系统的功能。动力学本身——无论是来自神经记录的经验数据还是来自神经模型网络动力学系统的合成数据——都可以被视为使用基于相关性的技术通过将它们投影到（高阶）网络上进行分析的数据。

高阶网络的新兴领域开辟了令人兴奋的新方向。虽然它有时可能看起来像是多个领域结果的拼凑而成，但我们相信相互促进可以带来很多收获；这篇综合评论和观点就是朝这个方向迈出的一步。我们期待未来看到这些研究方向的成果。