矩阵力学的构造见于著名的玻恩—海森堡—约当矩阵力学三部曲（1925），和狄拉克的一篇论文（1925）。玻恩与约当1930年合著的Elementare Quantenmechanik（基础量子力学）对矩阵力学作了详细的阐述。矩阵力学源起理解原子谱线强度的努力，关键是对频率求和规则借助类比方法的量子改造。矩阵力学的思想基础说到底是傅里叶分析，那是跨度达两千年的人类智慧结晶。矩阵力学延伸了矩阵的算法。泡利于1926年使用矩阵力学解氢原子问题。

1  引 子

本系列的目的是介绍量子力学的具体创立过程，实现这一目的手段是对创立者所发表论文的解读与引用。当然，由于篇幅所限与笔者能力所限，我们的引用是片面的，解读也是片面的，还会包含一些错误。本系列会尽可能地提供原文、译文的出处，建议阅读恰当的参考文献作为补充，敬请读者拨冗亲自阅读以形成自己的判断。在引文或转述的部分，笔者添加的自己的话会用{}括上，以免被误解为原文作者的意思。英文引文一般不作翻译。

本篇解读量子力学之矩阵力学形式。有趣的是，一般量子力学教科书甚至都不提矩阵力学，而偏偏矩阵力学才反映量子力学出现的必然性，也是量子力学的精髓所在，AB≠BA；[q,p]=iℏ1；矩阵形式的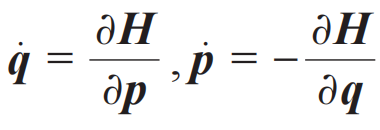

；以及波动力学用到的p=-iℏ∂，这些都是矩阵力学得到的结果。但是，矩阵力学很难懂，连温伯格（Steven Weinberg，1933—2021）这样的物理学巨擘都觉得难懂。在Dreams of a Final Theory（Pantheon Books，1992）一书中，温伯格这样写道：“If the reader is mystified at what Heisenberg was doing, he or she is not alone. I have tried several times to read the paper that Heisenberg wrote on returning from Helgoland, and, although I think I understand quantum mechanics, I have never understood Heisenberg’s motivations for the mathematical steps in his paper”。这倒也道出来了问题的根源，从the paper that Heisenberg wrote on returning from Helgoland是肯定弄不懂矩阵力学的。温伯格这样的物理学巨擘承认自己不理解海森堡论文中的那些数学步骤，可能与他不关注人们理解原子谱线之宽度与明锐度特征（图1）的努力有关。这些应该是原子物理教科书的内容，当然原子物理教科书里也没有。海森堡在慕尼黑大学当学生时即跟随索末菲（Arnold Sommerfeld，1868—1951）研究谱线的宽度与明锐度问题，见于文献：

[1] Arnold Sommerfeld，Werner Heisenberg，Bemerkungen über relativische Röntgendubletts und Linienschärfe（关于相对论性伦琴双线以及谱线明锐度的说明），Zeitschrift für Physik 10，393（1922）；

[2] Arnold Sommerfeld，Werner Heisenberg，Die Intensität der Mehrfachlinien und ihre Zeeman-Komponenten（多重谱线的强度与谱线的塞曼分量），Zeitschrift für Physik 11，131（1922）.

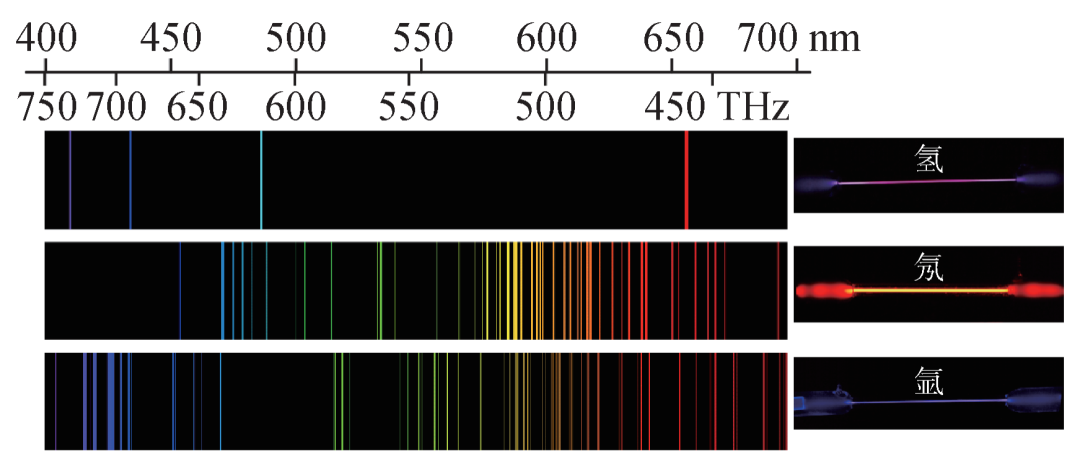
图1 原子谱线。观察后思考，会发现光谱线有如下特征需要表征，包括谱线的位置（频率）、谱线的强度（包括强度为0的情形）、谱线的宽度、精细结构，以及谱线对外加电磁场的响应（Zeeman effect，Stark effect），等等

毫无疑问，海森堡1925年思考的问题是他在慕尼黑研究工作的继续。海森堡1920年入慕尼黑大学学习，1922年即发表如此水平的论文，可见学术传承的重要前提是有学术可供传承。索末菲是量子论的奠基人之一，他通过本人以及门下一众学生对近代物理的建立厥功至伟。

欲弄懂矩阵力学，得读玻恩—约当以及狄拉克1925年的文章以及玻恩—约当1930年的专著Elementare Quantenmechanik（基础量子力学）。不是基于原作者的原始论文而是基于后来出现的回忆录、报告、通信以及文化学者们的研究闲谈，是一些涉及矩阵力学的学术论述的通病。比如，不来梅大学的Günter Ludyk在Quantum Mechanics in Matrix Form（Springer2018）一书中写道：“When returning from Helgoland（where he first had this crucial idea）to Göttingen, Heisenberg found out that the operations he applied to these tables were well known to mathematicians. The tables were called matrices, and the operations that he used to get from the table representing the electron velocity to the table representing the square was named matrix multiplication”，这纯属信口开河。在1925年那一年，海森堡不知道矩阵乘法，也没几个数学家知道矩阵。在1925年海森堡一人署名的文章（不是他一人写的）中，矩阵一词就没出现过，而建立矩阵力学的第一篇文章，包含矩阵算法与基于矩阵的量子力学推导的，作者为玻恩和约当。笔者多年前曾言：“数学是物理学的语言，是物理学的工具，也是物理学的目的（之一）”。矩阵力学之于矩阵数学，就是支撑第三条的例子。欲建立起矩阵力学，不仅要知道矩阵算法，还得发展矩阵算法——量子力学表述有发展矩阵算法的需求。对这一点，玻恩、约当和狄拉克都做出了不同的贡献。

现实是，虽然一年后有了波动力学还有了矩阵力学与波动力学等价的（错误）说法（见后续文章），矩阵力学远不如波动力学那么popular。人们当时欢迎波动力学，以及后来的量子力学基本上都被表现成波动力学形式，是因为把薛定谔方程换成求本征值、本征函数的形式就是纯粹经典的数学物理方程问题了，连一点量子力学的味儿都没有。

2  矩 阵

矩阵是一个了不起的数学概念。Matrix，拉丁语的本义是子宫（womb），与mater（母亲）同源。1850年，英国数学家James Joseph Sylvester（1814 — 1897）造了matrix这个词 [ Additions to the articles in the September number of this journal, “On a new class of theorems,” and on Pascal’s theorem, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 37, 363—370（1850）]。在第369页上有句云：“For this purpose, we must commence, not with a square, but with an oblong arrangement of terms consisting, suppose, of m lines and n columns. This does not in itself represent a determinant, but is, as it were, a Matrix out of which we may form various systems of determinants…”. 此外，“I have in previous papers defined a‘Matrix’as a rectangular array of terms, out of which different systems of determinants may be engendered as from the womb of a common parent [The Collected Mathematical Papers of James Joseph Sylvester：1837—1853, Paper 37, p. 247]”定义了项的矩形阵列，之所以名之为matrix，因为就像从母亲的子宫产生孩子一样从这个矩形阵列中可以产生出不同的systems of determinant。笔者之所以不逐字翻译上述这段话，是因为我不知道该怎么翻译这里的determinant一词，我只知道当前的“矩阵值”译法肯定不对。从一个matrix产生出不同的systems of determinant，指的是从一个矩阵中可以划出不同的minor（汉译余子式）。

矩阵概念的提出，应该与线性方程组有关。如今我们把n-个未知数写成x=（x1, x2, …, xn）的形式，则线性方程组可以简写为M∙x=c，其中c=（c1, c2, …, cn）是一组常数，而M是n×n个常数，排成一个方形阵列，就是英文的square matrix。Square matrix，方阵，看看这里出现的情景，它是不是对应方程啊。程，度量衡总称。《九章算术》卷八云：“程，课程也。群物总杂，各列有数，总言其实。令每行为率。二物者再程，三物者三程，皆如物数程之。并列为行，故谓之方程。行之左右无所同存，且为有所据而言耳。此都术也，以空言难晓，故特系之禾以决之。又列中、左行如右行也”。当然啦，我们把方程M当成了M∙x=c这个事物的整体，对应英文的equation，德文的die Gleichung。然而，西文的equation，die Gleichung，字面上是等式的意思，故他们学方程（等式）的时候自然而然地会关联上恒等式（identity）和不等式（inequality）。似乎咱们学方程的时候又吃亏了不少。

矩阵作为某些对象（实数、复数等）的阵列，本身也可以作为一个对象，有属于它的代数（加法与乘法）。矩阵满足结合律和分配律，但是一般来说不满足交换律。这恰是它能在量子力学中发挥作用的原因。量子力学的一个被传得神乎其神的特点不过就是物理量（算符）的非交换性（满足非交换代数。其实转动在经典力学里一样遵从非交换代数），矩阵正好有这个性能。一个方矩阵，具体地可写成如下形式：

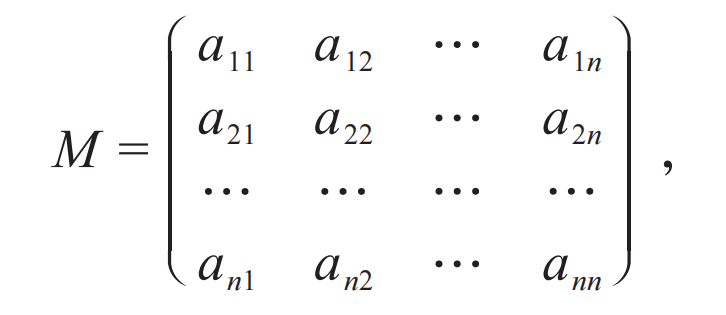
这里的矩阵元aij的指标选取（i, j=1,2,…n）具有一定的任意性，比如把上式改写成

也没关系。不过，当指标（ij）联系着其他物理量时，比如是和一个einωt因子结合在一起的，如何选择就有讲究了。你会看到在矩阵力学中，合适的矩阵的标记应该是

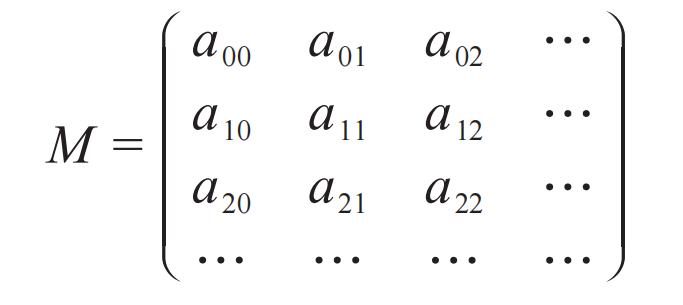
的样子，即指标选为（i, j=0,1,…n）。矩阵力学的底色是傅里叶分析，傅里叶分析是和周期性存在相联系的。后来的量子力学教科书对这个问题没有感觉，其作者可能根本不知道量子力学在干嘛。

为了用矩阵表示量子力学，光知道矩阵这个概念，甚至还知道矩阵的加法与乘法，那是远远不够的。至少，还应该会熟练地对矩阵作为其他变量的函数以及矩阵作为变量的函数做微积分才行，这也是为什么笔者要强调是约当和狄拉克这两个人对矩阵力学做出重大贡献的原因。没错，是约当和狄拉克这种学数学出身的年轻人对构造矩阵力学做出了重大贡献。年轻不是创造的本钱，年轻时学到了真本领才有创造的可能。

3  加速电荷的辐射问题

1887—1888年，德国人赫兹（Heinrich Hertz，1857—1894）在实验室产生了电磁波，这应该是电动力学历史上的一个关键节点。1897年，电子的身份被汤姆孙（J. J. Thomson，1856—1940）确立，这是电动力学历史上的另一个关键节点。这样，电动力学的面貌改变了。从前的电动力学是电流的电动力学，现在要研究带电粒子的电动力学，而且要研究其辐射行为。这段时间的研究者有丹麦人Ludvig Lorenz（1829—1891），荷兰人Hendrik Antoon Lorentz（1853—1928），英国人Joseph Larmor，法国人Alfred-Marie Liénard与德国人Emil Wiechert，等等。英国数学家、物理学家拉莫（Joseph Larmor，1857—1942）的三篇同名文章中有关于加速电荷会产生辐射的理论，结论是加速电荷发射的功率为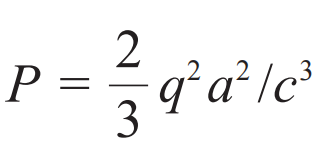

，其中a是加速度。这三篇文章为：

[1] Joseph Larmor, A dynamical theory of the electric and luminiferous medium, Philosophical Transactions of the Royal Society 185, 719—822（1894）；

[2] Joseph Larmor, A dynamical theory of the electric and luminiferous medium, Part II, Proceedings of the Royal Society of London 58, 222—228（1895）；

[3] Joseph Larmor, A dynamical theory of the electric and luminiferous medium, Part III, Philosophical Transactions of the Royal Society 190, 205—300（1897）.

1900年，拉莫出版了Aether and matter（Cambridge University Press）一书，书里有他关于这一段时间电动力学研究的总结。

关于加速电荷的辐射问题，另有法国物理学家Alfred-Marie Liénard（1869—1958）在1898年发表的三部分文章[A. Liénard, Champ électrique et magnétique produit par une charge concentrée en un point et animée d'un mouvement quelconque（集中于一点的、处于某种运动的电荷所产生之电磁场），L'Éclairage Électrique 16（27,28,29）, 5—14, 53—59, 106—112（1898）]，其中给出了电磁势的表达，且是相对论版的，可以用来计算辐射的分布。1900年，德国人Emil Wiechert（1861—1928）也独立发表了同样的结果[E. Wiechert, Elektrodynamische Elementargesetze（电动力学基本定律），Archives Néerlandaises 5, 549—573（1900）；重刊于Annalen der Physik 309（4），667—689（1901）]。这个电磁势的表达被称为Liénard—Wiechert势。在低速情形，由Liénard—Wiechert势可以得到拉莫的结果。

拉莫的结果，即加速的电荷辐射电磁波，被称为Larmor Proposition（拉莫命题），但并不特别令人信服。原子核就在转动，但并不辐射。根据广义相对论，加速度等价于一个均匀的引力场，不理解为什么加上一个引力场后一个本不辐射的电荷就辐射了。人们相信，也许应该说在某些情形下加速电荷会辐射电磁波。当然，来自原子的辐射还显示出分立谱的特征，更是同已有理论不符。

玻恩、海森堡、约当的矩阵力学，考察的是电子辐射问题。其首要问题是加速电荷辐射之高阶项在量子论中该如何表示的问题。至于这些辐射的高阶项公式来自谁的推导，笔者尚未找到确切的、一对一的出处。这些公式的表达，德语原文和英文译文似乎都有错误（见下）。

4  克拉默斯的色散关系

在量子力学出现的临界时刻（1924—1925），一个值得关注的关键人物是荷兰物理学家克拉默斯（Hendrik Anthony Kramers，也称Hans Kramers，1894—1952），见图2。克拉默斯于1912—1916年在莱顿大学学习数学与物理，然后到哥本哈根自报家门（visit unannounced）跟随玻尔（Niels Bohr，1885—1962）做博士研究，但是却是在埃伦费斯特的名下于1919年在莱顿大学获得的博士学位（此处也可见同德语国家学位制度的不同）。克拉默斯的博士论文题目为“Intensiteit van Spectraallijnen”，但论文内容是英文的，英文题目为“Intensities of Spectral Lines”，笔者猜测这是为了照顾到丹麦—荷兰两方面的缘故。其内容，如其所言，为“On the application of quantum theory to the problem of the relative intensities of the components of the fine structure and of the Stark effect of the lines of the hydrogen spectrum（关于量子理论在氢谱线的精细结构与斯塔克效应的各单元之相对强度问题上的应用）”，这个句式连同the的用法真让人受不了。

图2 Hans Kramers在上课（约在1921年）

关注原子谱线的相对强度是催生量子力学的关键。据克拉默斯所言，玻尔1918年有篇论文说基于量子理论可以回答谱线的极化（偏振）和强度问题[不知道是不是指玻尔的Drei Aufsätze über Spektren und Atombau（论谱与原子结构三篇）]。笔者浅见，似乎后来的理论对谱线偏振的诠释不怎么令人信服，或者靠自旋概念就给解决了？光的偏振是表现在物理空间的，但我们又说自旋是内禀自由度。这问题此处放下不提。

1924年3月25日，克拉默斯自哥本哈根发出一篇文章[H. A. Kramers, The Law of Dispersion and Bohr’s Theory of Spectra, Nature 118, 673—674（1924）]，讨论色散关系。1924年1月5日，克拉默斯和海森堡自哥本哈根发出一篇文章[H. A. Kramers, W. Heisenberg, Über die Streuung von Strahlung durch Atome（ 论 原 子 对 光 的 散 射），Zeitschrift für Physik 31（1）, 681—708（1925）]，得出了著名的Kramers—Heisenberg色散公式。这就是玻恩构造量子力学时一再引用的克拉默斯与海森堡的色散关系。奇怪的是，这篇文章竟然延宕了13个月才发表。

样的公式只对频率不在吸收或者发射线上且相角很小的情形才成立。

爱因斯坦在1916—1917年发展了一套辐射的概率理论（probabilistic radiation theory），这指的是爱因斯坦为得到黑体辐射普朗克公式所作的努力。爱因斯坦的这个模型提供了研究辐射—原子相互作用的出发点。

关于色散问题的研究，拉登伯格（Rudolf Ladenburg，1882—1952）为此持续忙碌了20年，发表了50多篇文章，例如后期的R. Ladenburg, F. Reiche, Dispersionsgesetz und Bohrsche Atomtheorie（色散规律与玻尔的原子理论），Die Naturwissenschaften 12（33）, 672—673（1924）; R. Ladenburg, F. Reiche, Absorption, Zerstreuung und Dispersion in der Bohrschen Atomtheorie（玻尔理论里的吸收、散射与色散）, Die Naturwissenschaften 11, 584—598（1923），等等。把原子看成虚谐振子的集合（a collection of “virtual harmonic oscillators”）是拉登伯格在1924年论色散理论的文章中隐性地提出的。

直到1925年，辐射与原子的相互作用都是量子理论的主题。研究主角有玻尔，斯拉特（John Clarke Slater，1900—1976）和克拉默斯，结果见于例如J. C. Slater，Radiation and Atoms, Nature 113, 307—308（1924）；N. Bohr, Atomic Theory and Mechanics, Nature 116, 845—852（1925）。这三人合作的论文[N. Bohr, H. A. Kramers, J. C. Slater, The quantum theory of radiation, Philosophical Magazine, Series 6, 47（281）, 785—802（1924）]被称为BKS理论，它不正确，但它在量子论发展史上非常重要。

以上两节里的内容是理解矩阵力学之所以发生的物理背景。玻恩在他1924—1925年的原子力学教程、提出量子力学概念的论文以及创立矩阵力学的论文中都一再强调克拉默斯的工作是不可忽略的。一般的科学史家会忽略这一点。至于关于矩阵的数学，笔者承认在阅读矩阵力学论文之前从未在那些linear algebra（线的代数。不是线性代数）书里见到过相关内容。关于1885—1924年期间关于谱线研究的论文，笔者未能深入研读以给出一个清晰的历史与物理内容的表述，甚为遗憾。

5  矩阵力学三部曲

1925年，德国哥廷恩大学的教授玻恩（Max Born，1882—1970）率同他的两位年轻助手海森堡（Werner Heisenberg，1901—1976）和约当（Pascual Jordan，1902—1980）投出了三篇文章，此即俗谓的矩阵力学三部曲，分别是：

[1] W. Heisenberg, Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen（运动学的与力学的关系的量子理论再诠释）, Zeitschrift für Physik, 33, 879—893, 1925（1925年7月29日收稿）；

[2] M. Born, P. Jordan, Zur Quantenmechanik（论量子力学）, Zeitschrift für Physik, 34, 858—888,1925（1925年9月27日收稿）；

[3] M. Born, W. Heisenberg, P. Jordan, Zur Quantenmechanik II（论量子力学 II）, Zeitschrift für Physik, 35, 557—615, 1926（1925年11月16日收稿）.

请注意这三篇论文的题目、作者署名及顺序、收稿日期，发稿地皆为哥廷恩！第一篇论文的题目是“运动学的与力学的关系之量子理论的再诠释”，而第二篇、第三篇是同一篇文章的两部分，题目为Zur Quantenmechanik，但作者从玻恩—约当两人调整为玻恩—海森堡—约当三人。纯从这三篇文章纸面上的题目和作者安排来看，笔者倾向于认为创立矩阵力学的还是玻恩（背后的故事以后再说）。一年前玻恩引入量子力学一词时，文章题目为Über Quantenmechanik。若认为Zur Quantenmechanik和Über Quantenmechanik这两者是同一个题目，都可以译为“论量子力学”，这没有问题。但是，Zur=zu+der，介词zu就是英文的to，故而若我把Zur Quantenmechanik译成“走向量子力学”，似乎更贴切，更能说明了点儿什么。当然，还是要看文章的内容到底在说什么。从前不方便拿到论文的德文原版，也没有英文译本，我们只能靠他人的三言两语引用来管中窥豹。现如今德文原文和英文译本都很容易从网上获得，我们还是要自己研读、自行判断才好。这三篇论文的原文以及流传的英译本都有（排版）错误，请朋友们阅读时注意。

5.1 第一篇
图3是矩阵力学三部曲第一篇的截图。这篇文章是海森堡写了个稿，于1925年7月9日交给玻恩寻求指导的[Abraham Pais, Niels Bohr’s times：in physics, philosophy, and polity, Clarendon（1993）; Helmut Rechenberg, Werner Heisenberg—Die Sprache der Atome（ 维 纳·海 森 堡 — 原 子 有 话 说），Springer（2010）]。至于玻恩添加了什么内容，以及最后这篇文章是谁人定稿的，笔者不详。对的，题目里面没有量子力学一词，正文中也只出现过一次“quantenmechanischen”的字样，而“矩阵”一词则从未出现过。对运动学的和力学的关系的再诠释或曰换个表达，目的是为一个基于原则上可观测量之间关系的“量子理论的力学（quantentheoretische Mechanik）”奠定基础。

图3 矩阵力学三部曲的第一篇。其中的文字为“运动学的与力学的关系的量子理论再诠释，来自哥廷恩的W. Heisenberg（1925年7月29日收稿）”

量子理论的形式规则（formale Regeln）对氢原子及其斯塔克效应（Stark effekt）是可用的，但是对置于交叉电磁场下的氢原子，或者多电子的原子，就不好使了。渐渐地，这些量子理论的计算规则——其本质上是以经典力学的应用作为特征的——的失效被看作是对经典力学的偏离（dieses Versagen der quantentheoretischen Regeln, die ja wesentlich durch die Anwendung derk lassischen Mechanikcharakterisiertwaren, als Abweichung von der klassischen Mechanik zu bezeichnen）。{请大家注意，至少到此时，量子理论的特征是经典力学}。这种偏离（Abweichung）的说法是无意义的。应该类比经典力学，建立一个量子论的力学{请按照机理、学问来理解}，其中只出现可观测量之间的关系。作为对这样的量子论的力学之首要的、最重要的Ansätze{可理解为建设基础，假设的前提，搭建结果。Ansatz（复数为Ansätze）来自动词ansetzen，就是setup。但是类似的德语词会同时表示过程与结果，比如在肚子上搭建的结果，Bauchansatz，就是啤酒肚。在另一个物理语境中，Ansatz被汉译为预设解}，除了频率条件以外，还有克拉默斯的色散理论以及相关工作。

5.2 第二篇
图4是矩阵力学三部曲第二篇的截图。这篇长31页的论文分为五个部分：导言；第一章，矩阵计算；第二章，动力学；第三章，检验非简谐振子；第四章，电动力学评论。文章的作者为玻恩和约当。此文目的是把海森堡上一篇论文中的Ansätze发展成量子力学的系统理论（zu einer systematischen Theorie der Quantenmechanik），数学工具是矩阵计算，力学的运动方程从变分原理导出，基于海森堡的量子条件可以由力学方程导出能量定理和玻尔的频率条件。{玻恩说此文会讨论分振动的相位（die Phase in den Partialschwingen）的意义。笔者提醒，对一个物理量作傅里叶展开，各分振动是否是独立的，相位是什么意思，这些是历史悠久的力学问题，也是导向量子力学的必经途径。一般的英文教科书里都不关注这个问题}。

图4 矩阵力学三部曲的第二篇。图中文字为“走向量子力学，来自哥廷恩的M. Born和P. Jordan（1925年9月27日收稿）”

海森堡为新的运动学和力学提出的Ansätze可理解为试图构建一个新的、确实契合的概念系统，而非借助或多或少人为的、硬性的同旧有概念的匹配（künstliche und gezwungene Anpassung der alten gewohnten Befriffe）以解释新的事实。因为有对他的思考尚在新生状态（in statu nascendi）就知晓的便利，因此在他的研究一结束我们俩就开始去弄清楚他的Ansätze的数学形式内容（Begünstigt durch den Umstand，daß wir seine Überlegungen schon in statu nascendi kennenlernen dürften, haben wir uns nach Abschluß seiner Untersuchungen bemüht, den mathematisch-formalen Gehalt seinerAnsätze zu klären）。{玻恩这么说，是因为在这个阶段玻恩是哥廷恩大学的教授，海森堡是他的助手，约当是他的学生及助手。海森堡写下了前一篇文章里的一些结果给玻恩看，玻恩先是请前助手泡利帮忙做其中的数学部分，泡利没有同意，后由约当接手完成。D. H. Delphenich的英文译文把“Begünstigt durch den Umstand，daß wir seine Überlegungen schon in statu nascendi kennenlernen dürften”翻译成“Encouraged by the fact that we can already understand his argument in statu nascendi”，不知是何居心。随便找个字典也会告诉你“Begünstigt durch den Umstand，…”大约对应英文的“having the advantage that…”。} 我们表明，在海森堡的基础上是可以达成一个既同经典力学明显密切类比又保证具有量子现象标签性特点的量子力学之闭合的数学理论大厦的（auf der von Heisenberg gegebenen Grundlage das Gebäude einer geschlossenen mathematischen Theorie der Quantenmechanik in merkwürdig enger Analogie zur klassischen Mechanik, doch unter Wahrung der für die Quantenerscheinungen kennzeichnenden Züge zu errichten）。

（1）矩阵计算

5.3 第三篇
这第三篇是对第二篇的延续，署名为玻恩—海森堡—约当三人，全文长59页（图5）。内容大致如下：第一章，单自由度系统；第二章，任何多自由度系统的理论的基础；第三章，与厄米特形式的本征值理论的关系{从时间上看，薛定谔1926年发表他的波动力学论文第一部分时应该没看到这篇。是否私下交流过，待考}；第四章，理论的物理应用。{这篇长文的数学部分和写作都是约当完成的。许多量子力学书甚至都不会提到约当这个名字，后续文章会回到这个问题}。

图5 矩阵力学三部曲的第三篇。图中文字为“走向量子力学II，来自哥廷恩的M. Born, W. Heisenberg和P. Jordan（1925年11月16日收稿）”

这篇文章太长，不方便在本文中详细分析。其最后部分把量子理论用于黑体辐射是亮点，笔者的《黑体辐射》对这部分未予充分重视，甚感遗憾。文章指出，量子论得出谐振子的能量为nhν，而这恰是普朗克要为空腔辐射预先假设的。文章说量子理论能证明分体积中熵的可加性（die Additivität der Entropiender Teilvolumina in der Quantenmechanik der Wellerfelder nachweisen könnte），这正是爱因斯坦得到辐射场能量涨落的重要出发点。许多方法能得到正确的普朗克公式，却不能得到正确的涨落表达。爱因斯坦的涨落公式里的一项是经典理论所没有的，量子理论补足了另一项{这部分请和爱因斯坦1917年的论文一起参详}。这篇文章还说，本没有什么反常塞曼效应（daß es also eigentlich gar keine anomalen Zeemaneffekte gebe）。大自然里本没有反常。如果物理学里有反常，那是物理学良心坏了。此外，论文中还用到了干涉涨落（Interferenzschwankungen），德拜统计（die Debyesche Statistik）等概念。

这篇论文的部分内容，后来在1930年的玻恩与约当合著的Elementare Quantenmechanik（基础量子力学）一书中以更加清晰的方式阐述了，读来更加易懂。试截取一段，方便读者朋友了解矩阵力学的初步基础。物理量q, p有傅里叶变换：

6  狄拉克对矩阵力学三部曲第一篇的响应

1925年对矩阵力学的建立有贡献的还有狄拉克（P. A. M. Dirac, 1902—1984）的一篇论文[P. A. M. Dirac, The Fundamental Equations of Quantum Mechanics, Proceedings of the Royal Society of London, Series A, 109（752）, 642—653（1925）]。这时的狄拉克，刚从工程数学专业转学物理不过两年。顺带说一句，狄拉克1926年提交了第一篇量子力学博士论文，成了历史上第一个量子力学博士，其导师为Ralph H. Fowler（1889—1944）。

海森堡的文章指出不是经典力学的方程有错，而是从方程得到物理结果的数学操作需要改变（the mathematical operations by which physical results are deduced from them require modification）。{下面这一段，解了我多年的困惑}。经典力学是这么干的。考察一个u自由度的力学系统，假设坐标表示成多重傅里叶级数的形式

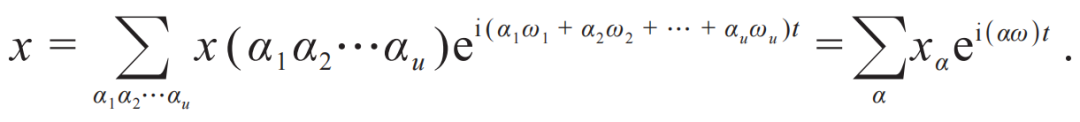
把这个表达代入运动方程，令两侧的任一简谐项的系数相等，得到的方程暂且称为“A-方程”，其解不是唯一的。振幅和频率可以表示为u个运动常数k1k2…ku的函数。每一个xα和（αω）都是一个两组数α和k的函数，记为xαk和（αω）k。

按照海森堡的提议，量子理论的解是这样的。依然是用eiωt的简谐分量表示，振幅和频率都用两组数表示，记为x（nm）和ω（nm）。对应此前的αr 可以认为是差nr-mr，但是k不知道该如何表示，它不能是单个n，m的函数。量子解是互锁的，必须当作一个整体看待（The quantum solutions are all interlocked, and must be considered as a single whole）。

一番论证后，容易得到频率条件，ω（nm）=Ω（n）-Ω（m）。狄拉克管Ω（n）叫做frequency levels（频率阶梯），它满足ω（nm）+ω（mk）=ω（nk）{有群论基础的读者会把这里的加法理解为乘法}。从经典的乘法关系：

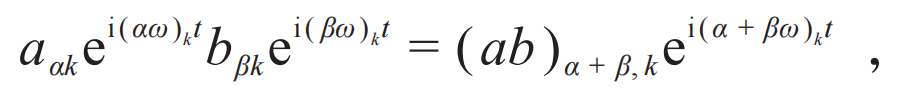
这个对振幅部分的表示要求有（ab）α+β,k=aαkbβk。对应的量子玩法可以是：

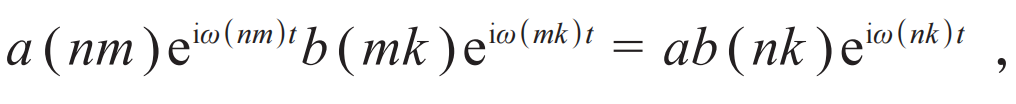
应有ab（nk）=a（nm）b（mk），这就是矩阵乘法。

7  泡利对矩阵力学的应用

泡利比海森堡大一岁，在慕尼黑大学索末菲那里是同门，又毕业后都给玻恩做过助手。海森堡在1925年思考如何计算谱线强度期间同泡利有过不少交流。实际上，玻恩看明白了海森堡论文中要用到的数学是矩阵，于是要求泡利来完成其中的数学部分的，但泡利拒绝了。矩阵力学三部曲发表后，泡利迅速跟上了这门新的力学，发表了[Wolfgang Pauli, Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik（新量子力学观点下的氢原子谱），Zeitschrift für Physik 36（5），336—363（1926）]一文，用它得到了氢原子光谱巴尔末项的表达。这成了第一个矩阵力学应用案例。泡利没有插手发展矩阵力学的事情，不知道泡利后来后悔过没有。笔者以为，如同狄拉克的论文，泡利这篇论文是对矩阵力学的发展，是矩阵力学的有机组成部分。

顺带说一句，泡利这篇工作显然受到了在汉堡大学为其做助手的教授楞次的影响。楞次（Wilhelm Lenz，1888—1957），不是楞次定律的那个楞次（Heinrich Lenz，或者Emil Lenz，1804—1865），以关于开普勒运动的研究而著名，名字写入了Laplace-Runge-Lenz矢量这个概念中。楞次研究开普勒运动的量子态[Wilhelm Lenz，Über den Bewegungsverlauf und Quantenzustände der gestörten Keplerbewegung（论受扰动开普勒运动的过程与量子态），Zeitschrift für Physik 24（1），197—207（1924）]，泡利借用这里的表述与方法进一步发展了矩阵力学。愚以为，楞次和泡利的两篇文章，加上薛定谔的波动力学解（数学上得到了外尔的帮助），构成了对氢原子问题（开普勒运动的量子版）的量子力学处理。一般量子力学教科书和史书会从玻尔的量子化条件直接给出个氢原子波函数了事，楞次和泡利的文章鲜有人提及。笔者修习原子物理和量子力学时，一直不明白从平面型的经典力学行星模型怎么就一下子跳跃到了氢原子的三维波函数描述，现在（2024.04.17）明白了这里根本没有跳跃，只是我不知道而已。也许，要求后来谈论量子力学的人具有起码的数学知识非常不合人情。如下是对泡利论文的摘录。

图6 泡利1926论文p.347上的截图

图7 泡利1926论文p.357上的截图

8  海森堡论及矩阵力学

图8 海森堡Die Physikalische Prinzipien der Quantentheorie一书p.79的截图

9  补充说明

矩阵力学源起于海森堡关于谱线强度的思考，由玻恩和约当构造而成，其系统性提升以及具体应用案例则是由狄拉克和泡利完成的。欲理解矩阵力学，本文介绍的海森堡（1925），玻恩—约当（1925），玻恩—海森堡—约当（1925），狄拉克（1925）和泡利（1926）这5篇文章是基础。由于篇幅和笔者水平所限，这里的介绍是远远不足以反映这些文章内容的全部。倘若有时间，笔者真想写一本《矩阵力学》的专著，因为在撰写本文的过程中我忽然注意到了量子力学的二象性，量子更多地见于矩阵力学，而力学（不是“力”学！）更多地体现在波动力学中。

矩阵力学来自对原子光谱的研究。关于后者，除了海森堡与索末菲的工作以外，拉莫和克拉默斯在这方面的工作非常关键。矩阵力学的不好懂，愚以为很大程度上是因为对这两位的忽视，当然也是因为相关的知识比较深刻而且麻烦。关于量子力学这门学问本身具有的矩阵力学~波动力学二象性，容笔者瞎说哈，将波动形式的函数（对应傅里叶分析）应用于Hamilton-Jacobi方程，得到薛定谔方程；将约当的关系p=-iℏ∂（来自矩阵力学）应用于薛定谔方程，得到经典力学的数理方程。波动力学之所以大受欢迎，是因为将关系p=-iℏ∂代入薛定谔方程后得到的，是在经典力学、经典电动力学中随处可见的数理方程，那不过就是二阶微分算符在不同维度、不同对称性的空间中的本征值问题而已。

笔者以为，矩阵力学是同经典力学、经典电动力学血肉相连的，是可见到如何构建量子力学的思想尝试的。此文中提到的5篇矩阵力学论文，玻恩、约当1930年合著的《基础量子力学》，狄拉克1930年著的《量子力学原理》，冯诺依曼1932年所著的《量子力学的数学基础》，可作为修习矩阵力学的绝佳参考。一本不包含矩阵力学部分的量子力学教科书，是有瑕疵的。

玻尔量子化条件里的量子数n，索末菲的研究表明它对应量子标签（nkm）中的k[或者是如今记号的（nlm）中的l ]。之所以会有这个错误插曲的发生，那是因为对于未加外场的氢原子，其量子状态是退化的（entarted，degenerated.汉译简并）。实验上加电场和磁场（文献中会表述为垂直的电场与磁场）会将退化去除（Aufhebung）从而让问题全面展现出来，泡利在利用矩阵力学求解氢原子问题时则是利用了pz，L2必须是对角阵从而引入对应的量子数。模模糊糊认识到体系存在退化，通过消除退化把问题充分表现出来得到关于问题的足够复杂的解，反过来了认识了什么是退化，这应该是科学方法论的一个有价值案例吧。

对应原理在矩阵力学的建立过程中扮演着重要的角色。然而，对应原理不是那些英文量子力学史或者量子哲学里字面上的对应原理，而是借助类比（Analogon）把经典色散关系写成量子论的表达形式，那才是量子力学的基石，见得学问创造者的功夫。

一个奇怪的现象，在当前这个阶段讨论原子物理，包括光谱、原子力学、矩阵力学和波动力学，一些著作似乎不能明确地区别电子的运动表述（坐标、动量、轨道或者角动量、Laplace-Runge-Lenz矢量、能量、跃迁概率等）与辐射提供的可观测量（包括谱线的频率、强度、宽度、偏振、精细结构、塞曼效应，斯塔克效应等）。电子（原子里的电子）与辐射（来自原子的辐射）是一个硬币的两面，那是一个硬币啊，那是两面啊。

历史上，矩阵力学三部曲之第一篇论文源起海森堡考虑谱线强度问题。海森堡把一些想法写下来交给玻恩，玻恩认识到这里面的矩阵问题，于是请数学比较好的泡利帮忙做数学演算部分。泡利没接受这件事，玻恩又转而让数学比较好但更年轻的助手约当来做。至于对这篇文章约当做了多少数学、写了多大的篇幅，笔者未见到具体可靠的文献。读者可将这篇论文与海森堡1927年自己写的关于不确定性原理的论文以及专著Der Teil und das Ganze（部分与整体）做个比较，看看有什么不一样。

矩阵表示有两个指标。关于跃迁过程，那是涉及两个状态的产生光的过程。所以，由跃迁过程导向矩阵力学的建立，有其内在的必然性。想起一个问题，就是有些人所谓的跃迁时间的问题，有人甚至把某个能级的寿命同两个能级之间跃迁所造成的谱线之宽度联系起来，并硬说这两者之间有倒数关系，不知道是如何忽视电子寿命是关于一个能级的问题（或者说一个能级相对所有其他能量更低能级的问题）而跃迁是关于两个特定能级的问题此一事实的？愚以为，谈论两个能级之间跃迁的过程（用时，time duration）是对跃迁过程的误解。跃迁何时发生有时间的问题，但电子跃迁不存在从能级1到能级2的问题。打个十分恰当的比喻。结婚是牵扯到一对男女的问题。虽然结婚相对于其他物理事件（比如钟表指针位置）是有确切的时间标记的，甚至这一对男女领结婚证的时间有先有后，但是他们成为法律意义上的一对夫妻在他们两人之间却是没有时间性过程的。电子跃迁，就发生时刻而言，对两个能级是不加区别的。

请允许我瞎说，狄拉克1928年提出相对论量子力学的工作是他关于矩阵力学工作的延续。相对论量子力学的关键是狄拉克矩阵。及至后来外尔（Hermann Weyl，1885—1955）和维格纳（Eugene Wigner，1902—1995）加入了量子力学表示的努力，所使用的工具是群论。群表示所使用的工具是矩阵。未来的关于强相互作用的盖尔曼（Murray Gell-Mann，1929—2019）的规范场论，其关键是Gell-Mann矩阵。矩阵对量子力学的意义，请读者朋友仔细掂量掂量。比如，愚以为矩阵力学对此后一年诞生的波动力学的重要意义是为其准备了概念系统。

为什么很多人提及量子力学时更愿意谈论“怪力乱神”？我猜测是因为未在经典力学和数学物理方面上下过功夫。就矩阵知识而言，笔者此前看过的矩阵分析的书，包括线的代数（不是线性代数！）的书，都没有达到玻恩—约当的高度，更没有提示我们可以象狄拉克那样，在需要时可以自创矩阵算法。我越来越厌恶那些把一个主题只是浮光掠影点到为止地介绍几句的书。如果你想谈论一个主题，请尽可能全面、深刻地谈论，懂不懂的那是读者的事情。但是，若作者只介绍一些皮毛还故意地暗示这是一出精彩大戏之全部，那就有点儿不太合适了！

参考文献
[1] Born M. Verlesung über Atommechanik（原子力学教程）. Springer，1925

[2] Green H S. Matrix Mechanics. P. Noordhoff Ltd.，1965 {作者是玻恩的学生，玻恩为本书做了序。不过，这本书中有很多不合事实的地方，比如关于普朗克是如何得到黑体辐射公式的。}

[3] Ludyk G. Quantum Mechanics in Matrix Form，1st ed. Springer，2018

[4] Mehra J，Rechenberg H. The Formulation of Matrix Mechanics and its Modification. In：The Historical Development of Quantum Theory，Vol. 3. Springer，1982

[5] Lewis E P（ed.）. The Effects of a Magnetic Field on Radiation：Momoirs by Faraday. Kerr and Zeeman. American Book Co.，1900

[6] Haar D T. Master of Modern Physics—The Scientific Contributions of H. A. Kramers. Princeton University Press，1998