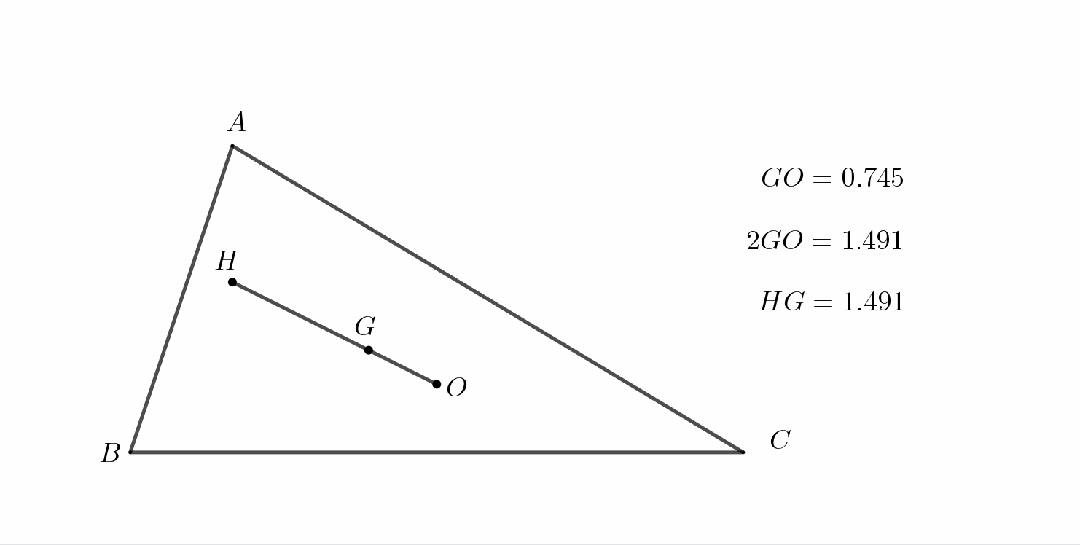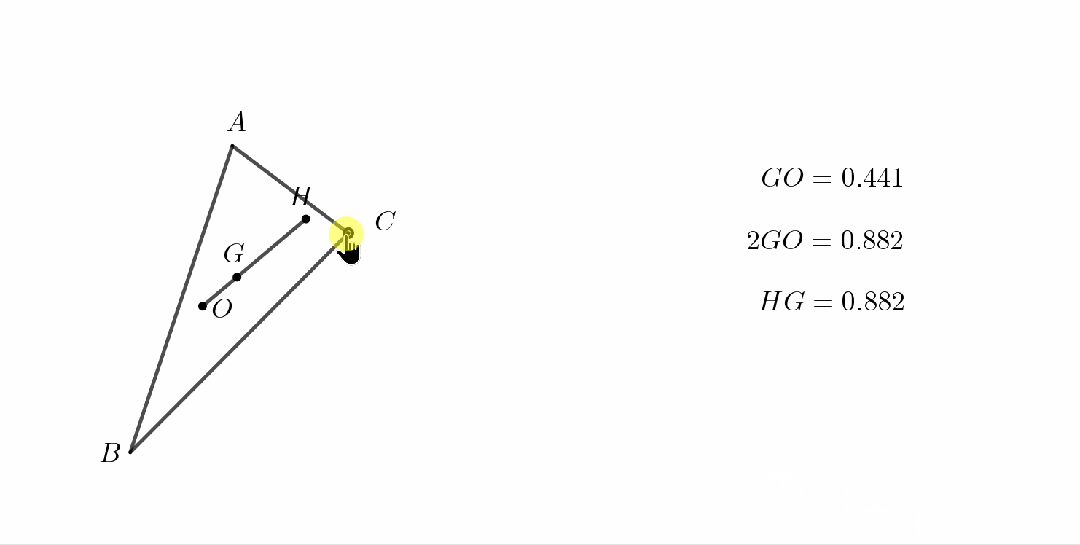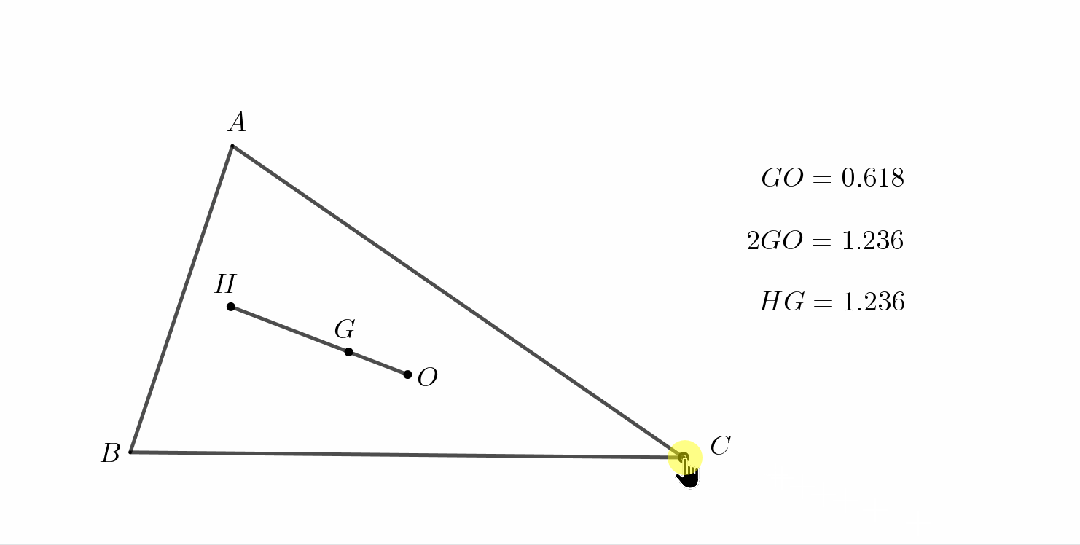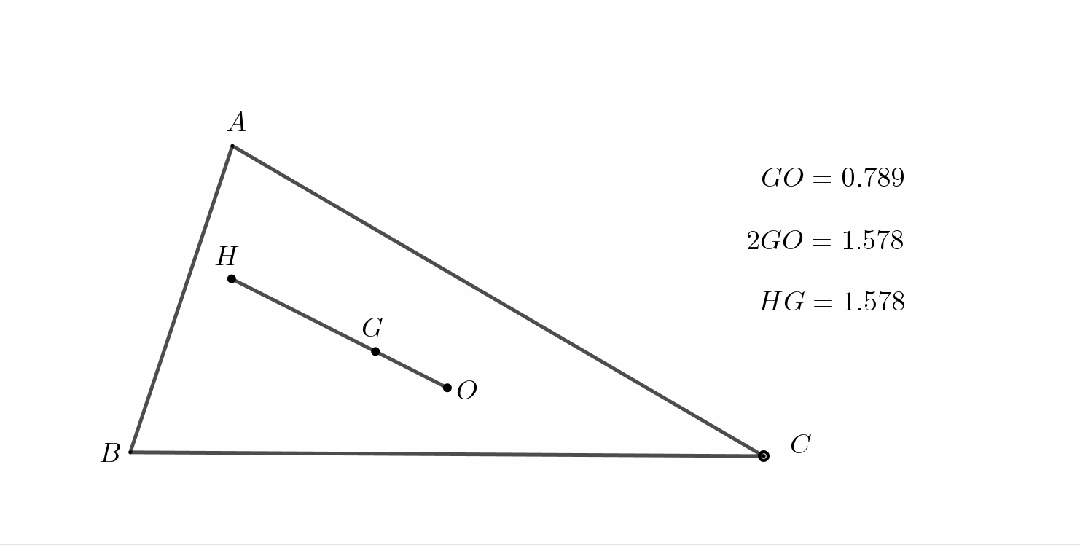
在平面几何中有一条有趣的结论:任意三角形的垂心H、重心G、外心O三点共线,且满足HG=2GO.此线由数学家欧拉发现,因此被称为欧拉线。

莱昂哈德·欧拉(1707~1783)
一个比较方便记忆这个结论的方法是观察特殊情况.我们可以构造一个直角三角形ABC,则显然垂心H与B点重合,外心O为斜边AC的中点.此时欧拉线即为斜边上的中线,显然有HG=2GO.
大数学家欧拉当时是如何发现并证明这个神奇的结论的呢?今天我们就来追寻大师的足迹,一起探索欧拉线的诞生过程.
1 欧拉线定理的证明
我们暂且将欧拉线定理的发现过程按下不表,让我们先来看一看欧拉在发现这个定理之后是如何巧妙地证明它的.这个证明被记录在《100个初等数学问题——历史和解》(100 Great Problems of Elementary Mathematics:Their History and Solution)一书中.


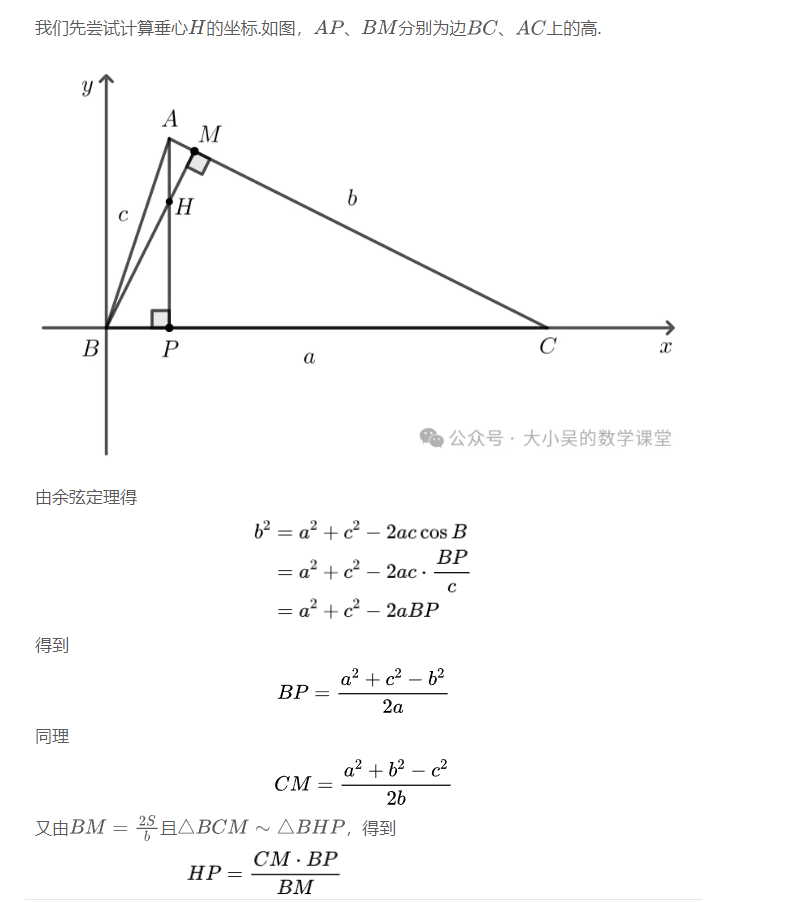
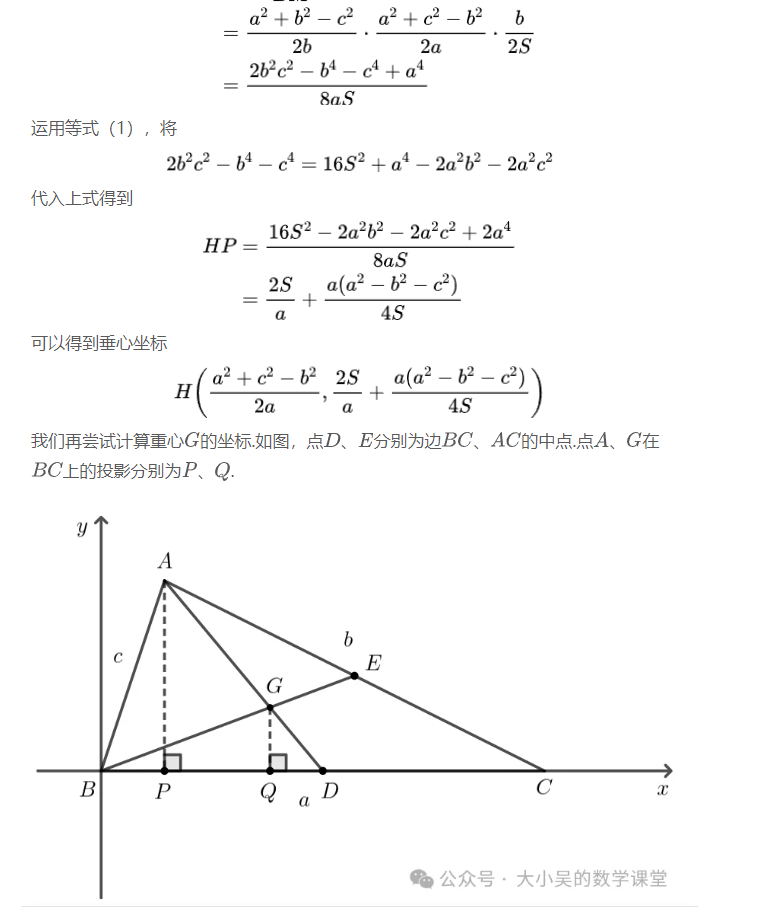


但是现在若仅仅通过观察这三个点的坐标根本无法知道垂心、重心、外心之间有何联系.
欧拉对这三个坐标进行了进一步的研究.在那个时代还没有发明出向量这样的数学工具.那么,欧拉唯一能做的,就是凭借其天才般的计算能力进一步研究这些点之间的距离关系.我们作为后来者重新走欧拉这条艰辛的计算之路,也难免不倒吸一口凉气.让我们跟随欧拉的脚步开始计算!


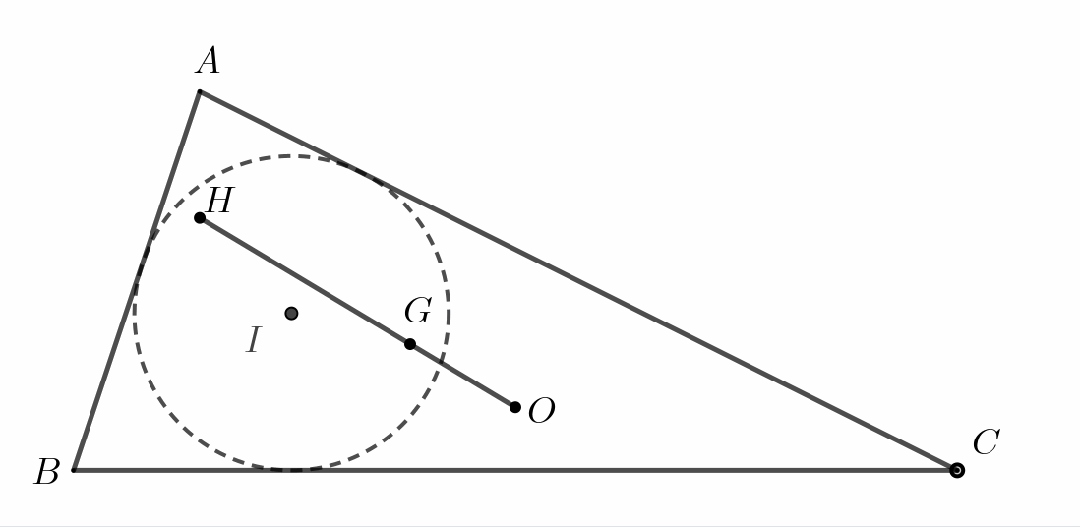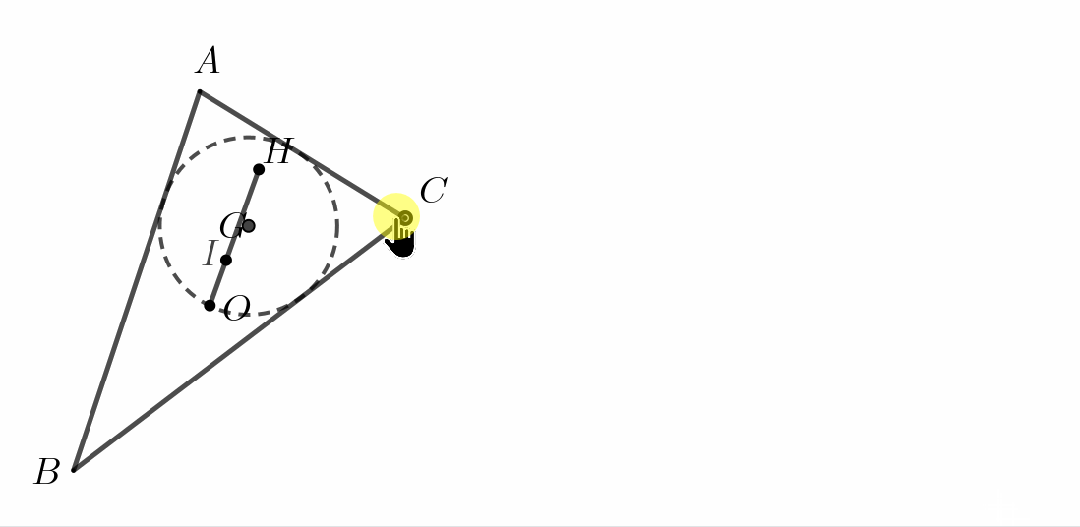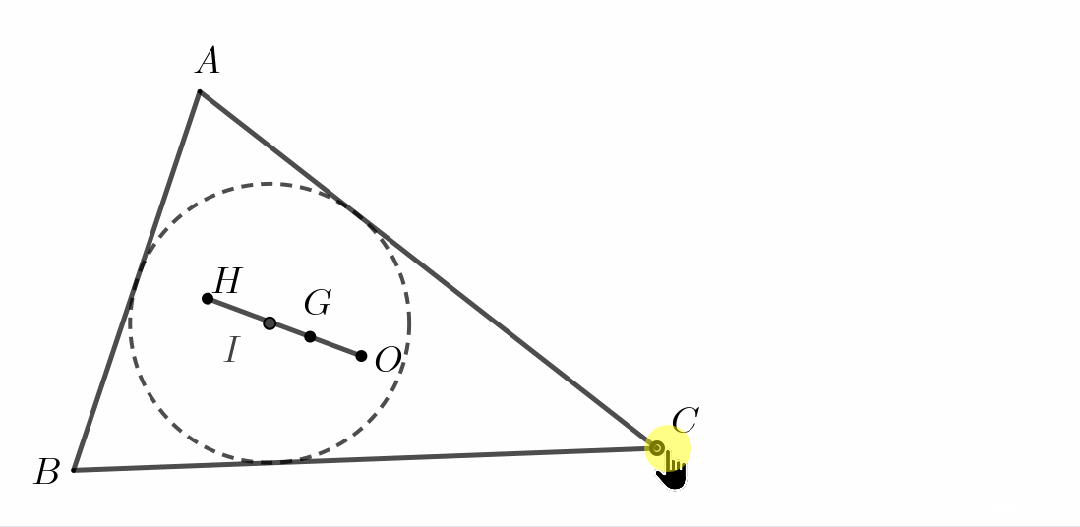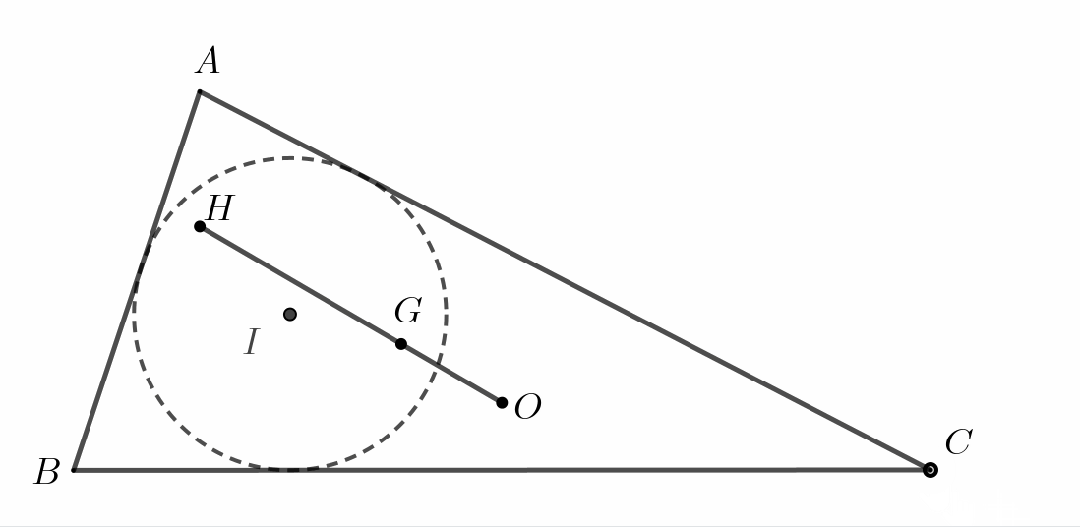
尽管如此,我们仍然可以从欧拉的工作中汲取智慧:一条数学定理的发现和证明过程很多时候难免会走一些弯路,即使是像欧拉这样的数学大师,刚开始的探索过程往往也可能是笨拙的.
我们学习数学要有探索精神,同时扎实地掌握计算基本功,对平时的一些问题(即便很小)要持续研究,不断对研究方法进行改进.想想欧拉这样的大数学家,他就不拒绝研究(欧拉线)这样的初等数学问题,一个个细小的积累最终使他成为青史留名的伟大数学家,欧拉的真实经历正印证了《劝学》中的名言:不积跬步,无以至千里.不积小流,无以成江海!
参考文献
[1]彭翕成.欧拉线的发现与证明[J].数学教学,2011(05):25-27+50.

















