自由能原理被认为是“自达尔文自然选择理论后最包罗万象的思想”，从第一性原理出发解释智能体更新认知、探索和改变世界的机制，被认为有可能成为智能的第一性原理的重要候选方案，并有望成为新时代复杂系统的大统一理论。

这篇2010年发表于 Nature Reviews Neuroscience 的综述论文是自由能原理提出者 Karl Friston 撰写的经典综述，引用量达7745，且仍在逐年上升。该综述从自由能原理视角审视了生物和物理科学中一些重要的大脑理论，包括贝叶斯大脑、预测编码和信息最大化原则、层次推理和注意力理论、神经达尔文主义、信息论和最优控制理论等，表明几种全局性大脑理论可能在自由能框架内得到统一。

斑图地址：https://pattern.swarma.org/study_group_issue/667

论文题目：
The free-energy principle：a unified brain theory?
论文地址：
https://www.nature.com/articles/nrn2787

最近提出的自由能原理可以解释行动、感知和学习。这篇综述从自由能的角度审视了生物科学（如神经达尔文主义（neural Darwinism））和物理科学（如信息论和最优控制理论）中一些重要的大脑理论。至关重要的是，有一个关键主题贯穿这些理论——优化。更进一步，如果我们仔细看优化的是什么，同一个量不断出现，即价值（value，预期奖励、预期效用）或其互补量，惊奇（surprise）（预测误差、预期成本）。这就是在自由能原理下被优化的量，这表明几种全局性大脑理论可能会在自由能框架内得到统一。

尽管神经科学领域有大量的实证数据，但关于大脑如何工作的整体理论却相对较少。最近提出的自适应系统的自由能原理试图为行动、感知和学习提供一个统一的解释。尽管这一原理被描述为统一的大脑理论[1]，但其统一不同脑功能观点的能力仍有待确立。本综述试图将一些关键理论纳入自由能框架内，希望找出共通的主题。我首先回顾了自由能原理，然后解构了几种全局性的大脑理论，以说明它们是如何表达相同的基本思想的。

1. 自由能原理

自由能原理（见框1）指出，任何与其环境处于平衡的自组织系统（self-organizing system）都必须使其自由能最小化[2]。该原理本质上是对自适应系统（即生物智能体，如动物或大脑）如何抵御自然无序趋势的数学表述[3-6]。接下来，我们将以非数学的方式探讨该原理的动机和涵义。我们将看到，尽管该原理的动机相当简单明了，但其涵义却复杂多样。这种多样性使该原理能够解释大脑结构和功能的许多方面，并使其有可能统一关于大脑如何工作的不同观点。在随后的章节中，我将讨论如何从这些角度将该原理应用于神经系统。这篇综述以一种相当抽象和技术性的方式开始，但随后试图用更熟悉的术语来解读基本思想。

动机：抵抗趋于无序的倾向。生物系统的决定性特征在于，面对不断变化的环境，它们仍能维持自身的状态和形式[3-6]。从大脑的角度来看，环境（environment）同时包括外部和内部环境（milieu）。这种秩序的维持可以在多个层面上观察到，并将生物系统与其他自组织系统区分开来；事实上，生物系统的生理几乎完全可以归结为它们的内稳态（homeostasis）[7]；更准确地说，有机体所能处于的生理和感知状态的库（repertoire）是有限的，这些状态定义了有机体的表型（phenotype）。从数学上讲，这意味着这些（内感受性和外感受性）感知状态的概率分布必须具有低熵；换言之，系统处于少数几种状态中任何一种的概率很高，而处于其余状态的概率很低。熵也是平均自我信息或“惊奇（surprise）”[8]（更形式化而言，它是结果的负对数概率）。在这里，“离开水的鱼”处于一种令人惊奇的状态（无论从感性上还是数学上）。

简而言之，生物的长期目标——保持自身状态在正常范围内——转化为在短期内避免出现惊奇。这里的“惊奇”不仅与当前状态有关，这无法改变，还与从一种状态到另一种状态的运动有关，而这是可以改变的。只要这些动作能够周期性地回到一些关键的、有利于生存的状态（例如在小误差范围内驾驶汽车），它就可以是复杂和游走的，这些关键的状态集合被称为“全局随机吸引子”（global random attractor）[10]。正是这些动作被自由能原理所优化。

到目前为止，我们所说的只是生物智能体必须避免“惊奇”，以确保它们的状态保持在生理范围内（更正式的论证见补充信息 S1）。但它们是如何做到这一点的呢？系统无法知道其感觉是否令人惊奇，即使知道也无法避免它们。这就是自由能发挥作用的地方：自由能是“惊奇”的上界，这意味着如果智能体最小化自由能，它们就隐含地最小化了“惊奇”。关键在于，自由能可以评估，因为它是智能体可以访问的两种事物的函数：其感觉状态，和由其内部状态（例如，神经活动和连接强度）编码的识别密度（recognition density）。识别密度是引起特定感觉的原因的概率表示。

这个（变分）自由能构造被引入统计物理学，将困难的概率密度积分问题转化为更容易的优化问题 [11]。它是一个信息论量（如“惊奇”），而不是一个热力学量。变分自由能已被用于机器学习和统计学，解决了许多推理和学习问题[12,13,14]。在这种情况下，“惊奇”被称为（负的）模型证据。这意味着最小化“惊奇”与最大化智能体存在的感官证据相同，如果我们将智能体视为其世界的模型。在当前语境，自由能提供了一个基本问题的答案：自组织的适应系统如何避免令人“惊奇”的状态？它们可以通过最小化自由能来做到这一点。那么，这涉及到什么呢？

影响：行动与感知。智能体可以通过两种方式减少自由能。它们可以通过对这个世界采取行动来改变感官输入，或者可以通过改变自身内部状态来改变识别密度。这种区分很好地对应了行动（通过外部干预改变输入）和感知（通过内部调整解释输入）的概念（框 1）。通过考虑自由能的三种数学等价形式，我们可以更详细地了解这意味着什么（数学处理方法见补充信息 S2（框））。

第一种将自由能表述为能量减去熵。这种表述重要的原因有三个：1. 它将信息论中使用的自由能概念与统计热力学中使用的概念联系起来。2. 它表明智能体可以评估自由能，因为能量是关于感觉及其感知原因共同发生的“惊奇”*，而熵则是智能体自身识别密度的不确定性或复杂度**。3. 它指出自由能基于对世界的生成模型（generative model），这个模型用感觉及其原因共同发生的概率来表达。这意味着智能体必须拥有一个内隐的生成模型，来理解不同原因是如何共同产生感官数据的。正是这个模型决定了智能体的性质，也决定了对惊奇的自由能约束的质量。

*译注：感觉指的是智能体从环境中获取的信息，如视觉、听觉或其他感官输入。感知原因则是智能体内部模型关于这些感觉是如何产生的解释。
**译注：识别密度的熵越高，智能体对自身模型的确定性就越低，意味着它对自己的预测和解释较为不确定。

第二种表述将自由能定义为“惊奇”和一个散度项（divergence term）之和。这里的（感知）散度项指的是识别密度（智能体对感觉原因的当前估计）与条件密度（或后验密度，即在给定感官信号的情况下，关于感觉原因的最佳猜测）之间的散度。两个密度之间的散度总是非负的，因此自由能是“惊奇”的上界。因此，通过改变识别密度（在不改变感觉数据的情况下）使自由能最小化，可以减少知觉偏差，这样识别密度就变成了条件密度，自由能就变成了“惊奇”。

第三种表述使用模型比较（model comparison）文献中的术语，将自由能表达为复杂性（complexity）和准确性（accuracy）的差值。复杂性是识别密度和先验密度之间的散度，也称为“贝叶斯惊奇”[15]，它反映了在吸收感官数据之前关于世界状态的信念（先验密度）与之后形成的信念（后验信念，由识别密度编码）之间的差异。准确性简单来说就是指在识别密度下预期的感觉有多少是准确的。通过改变感官数据（不改变识别密度）来最小化自由能，能够提高智能体预测的准确性，即智能体会有选择性地采样它所期待的感官输入，这被称为主动推理（active inference）[16]。这个过程的一个直观例子（当它上升为意识时）是在黑暗中摸索前进：我们预测下一步可能会触摸到什么，然后尝试确认这些预期。

总结来说，自由能基于一个关于如何生成感觉数据的模型以及对该模型参数（即感官原因）的识别密度。只有通过改变识别密度来改变关于被采样内容的条件期望，或者通过改变感官样本（即感官输入）使其符合期望，才能减少自由能。接下来的讨论将在一些关于大脑的关键理论的背景下考虑这些含义。

方框1：自由能原理

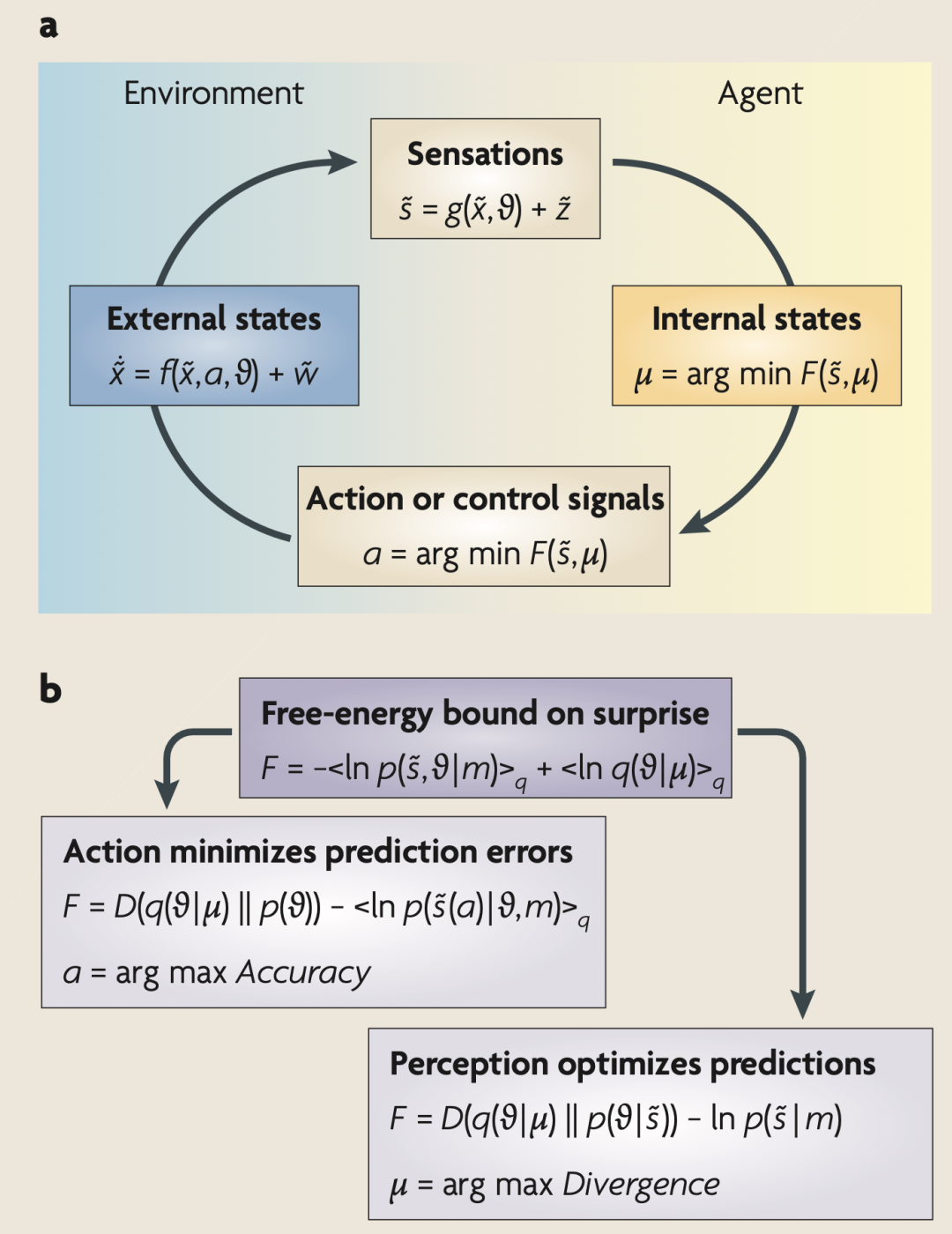
a部分表示定义自由能的各个量之间的依赖关系。这包括大脑的内部状态μ（t），及描述其与环境交换的量：感觉信号s（t）（及其运动），再加上动作 a（t）。环境由运动方程描述，这些方程指定了环境隐藏状态的轨迹。感知输入的原因包括隐藏状态 x（t）、参数θ以及控制随机涨落幅度 z（t）和 w（t）的精度 γ 。大脑的内部状态和动作使自由能 F（ ̃s,μ）最小化，自由能是感知输入和其原因的概率表示 q（θ|μ）的函数。这种表示被称为识别密度（recognition density），由内部状态编码。自由能取决于两个概率密度：识别概率密度 q（θ|μ）和生成感知输入及其原因的概率密度 p（ ̃s,θ|m）。后者表示一个概率生成模型（用m表示），其形式由智能体或大脑决定。

b部分提供了自由能的另一种表达式，以显示其最小化过程包含的内容：动作只能通过提高准确性（即选择性地采样被预测的数据）来减少自由能。相反，优化大脑状态使得表征成为感知输入原因的近似条件密度。这使得动作能够避免惊奇的感知遭遇。下面提供了一个更形式化的描述。

优化充分统计量（表征）

优化识别密度使其成为感知数据原因的后验或条件密度：这可以通过将自由能表示为惊奇  –In p（ ̃s,| m）  加上识别密度和条件密度（由图中的“内部状态”编码）之间的 Kullback-Leibler 散度来看出。因为这个散度总是正的，所以最小化自由能使得识别密度成为一个近似的后验概率。这意味着智能体以贝叶斯最优的方式隐式地推断或表征其感觉样本的诱因。同时，自由能成为惊奇的一个紧界，通过动作使其最小化。

优化动作

通过最小化自由能对环境采取行动，强制采样与当前表征一致的感知数据。这可以通过将自由能重新排列为准确性和复杂性的求和来看出。关键的是，动作只能影响准确性（由图中的“外部状态”编码）。这意味着大脑将重新配置其感觉上皮（epithelia），以采样识别密度预测的输入——换句话说，最小化预测误差。

2. 贝叶斯大脑假说

贝叶斯大脑假说（Bayesian brain hypothesis）[17]利用贝叶斯概率论将感知表述为一个基于内部模型或生成模型的建构过程。其基本思想是，大脑有一个关于世界的模型 [18-22]，它试图利用感官输入来优化这个模型[23-28]。这一观点与合成分析（analysis by synthesis）[20]和认识论自动机（epistemological automata）[19]有关。在这种观点中，大脑是一台推理机器，会主动预测和解释自己的感觉 [18,22,25]。这一假说的核心是一个可以生成预测的概率模型，通过对感觉样本进行测试来更新关于其原因的信念。这个生成模型被分解成似然（感觉数据的概率，给定其原因）和先验（这些原因的先验概率）。然后，感知成为反转似然模型（likelihood model，从原因到感觉的映射）的过程，以获取给定感觉数据的原因的后验概率（从感觉到原因的映射）。这种反转与最小化识别密度和后验密度之间的差值以抑制自由能是一样的。事实上，人们发展自由能公式是为了将精确推理的难题转化为一个更容易的优化问题，从而使其变得更简单[11-14]。这为模型识别和比较提供了一些强大的近似技术（例如变分贝叶斯或集成学习（Ensemble learning）[29]）。贝叶斯大脑假说中存在许多有趣的问题，自由能原理可以揭示这些问题；我们将重点讨论其中两个问题。

首先是生成模型的形式及其在大脑中的表现形式。对贝叶斯方法的一种批评是，它们忽略了推理所必需的先验信念是如何形成的[27]。然而，这种批评在层次化生成模型中就不存在了，因为其中先验信念本身就是最优的[26,28]。在层次化生成模型中，一个层级的原因会产生下一个层级的次要原因；感官数据本身是在最低层级产生的（方框2）。自由能的最小化实际上优化了经验先验（即在考虑到上一层级原因的情况下，某一层级原因发生的概率）。最重要的是，由于经验先验值是按层级联系的，因此它们会受到感官数据的影响，从而使大脑能够在线优化其先验预期。这种优化使层级结构中的每个层级都对其他层级负责，从而在多个描述层级上提供内部一致的感官原因表征。层级模型不仅在统计学（例如随机效应（random effects）和参数经验贝叶斯模型（parametric empirical Bayes models）[30,31]中发挥着重要作用，而且由于大脑皮层感觉区域的层次排列，大脑也可能使用层级模型[32，33，34]。

方框2：大脑中的分层信息传递

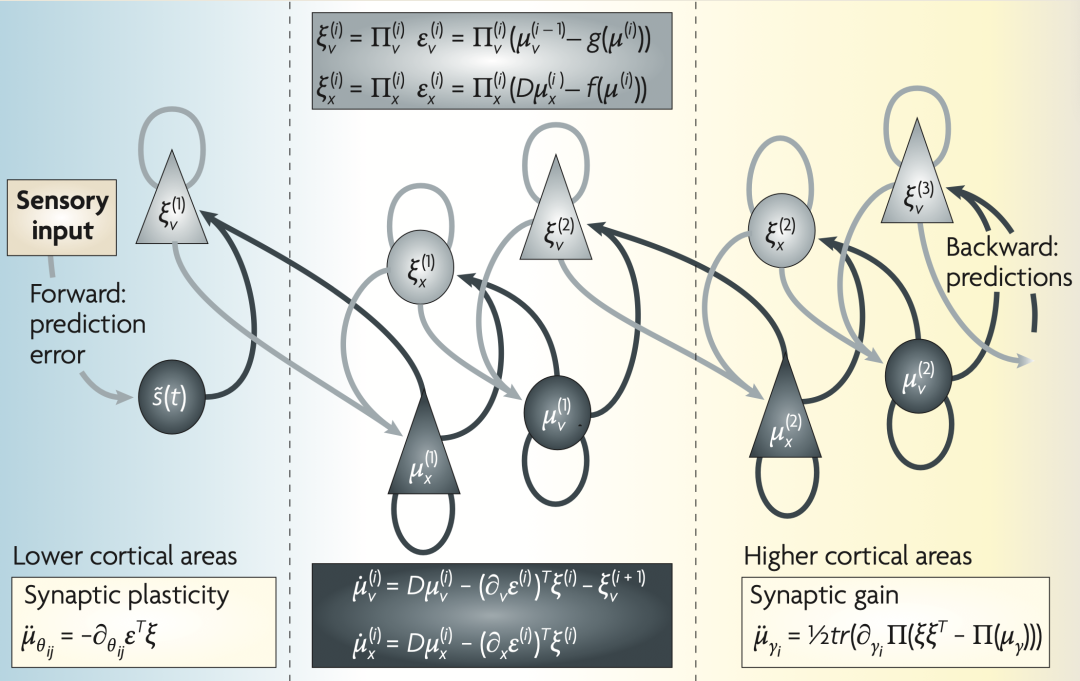
这幅图详细描述了一种神经元结构，它在感觉输入的分层模型中优化原因的条件期望。图中显示了前向驱动连接的潜在起源细胞（灰色箭头），这些连接从较低区域（例如外侧膝状核）传递预测误差到较高区域（例如V1），以及构建预测的非线性反向连接（黑色箭头）[41]。这些预测试图解释掉较低层次的预测误差。在这个方案中，前向和反向连接的来源分别是表浅和深层的金字塔形细胞（上三角和下三角），其中状态单元为黑色，错误单元为灰色。方程式代表使用下面的生成模型对自由能进行梯度下降的过程。上面的两个方程描述由错误单元编码的预测误差的形成，下面的两个方程表示识别动力学，使用自由能的梯度下降。

第二个问题涉及到大脑如何通过其物理属性（如突触活动、效能和增益）编码识别密度。一般情况下，任何概率密度都是通过其充分统计量（sufficient statistics）（例如高斯分布的均值和方差）来编码的。大脑编码这些统计量的方式对于支持识别的方案施加了重要约束：这些方案既包括形式自由的方案（例如粒子过滤（particle filtering）[26]和概率群体编码（probabilistic population codes）[35,36,37,38]），它们使用大量的充分统计量，也包括更简单的形式，它们对识别密度的形状做出更强的假设，以便可以用少量的充分统计量进行编码。最简单的假设形式是高斯形式，它只需要条件均值或期望——这被称为拉普拉斯假设（Laplace assumption）[39]，在该假设下，自由能仅仅是模型预测和被预测的感觉或表征之间的差异。最小化自由能则对应于解释掉预测误差。这被称为预测编码，已成为理解皮层层级之间神经元信息传递的流行框架[40]。在这种方案中，预测误差单元将条件期望（即当前层级对感觉原因的估计）与自上而下的预测（大脑对即将接收到的感觉输入的期望）进行比较，以详细说明预测误差。这个预测误差被传递到更高层级的单元，这些单元编码条件期望，优化自上而下的预测以解释掉（减少）下一层的预测误差。这里的“解释掉”仅仅意味着用由自上而下的预测驱动的抑制性突触输入来抵消预测误差神经元的兴奋性自下而上的输入（详细讨论见方框2和参考文献[41,42]）。这种自下而上的预测误差与自上而下的预测之间的交互影响持续进行，直到所有层级上的预测误差被最小化且条件期望被优化。这种方案已被用来解释早期视觉反应的许多特征[40,43]，并为电生理学中的重复抑制（Repetition Suppression）和不匹配反应（Mismatch Responses）提供了一个合理解释 [44]。图1提供了一个使用这种方案进行感知分类的例子。

重复抑制（Repetition Suppression）是指当相同的刺激被重复呈现时，大脑中相应的神经活动逐渐减弱的现象。这被认为是大脑对熟悉刺激的一种适应反应，反映了神经系统对重复信息的高效编码。

粒子滤波（Particle Filtering）是一种序列贝叶斯滤波方法，用于估计动态系统的状态，它通过一组随机样本（粒子）来代表后验概率密度。粒子滤波不需要假设状态空间或噪声过程遵循特定的分布（例如，高斯分布），使其成为一种灵活的非线性和非高斯滤波方法。

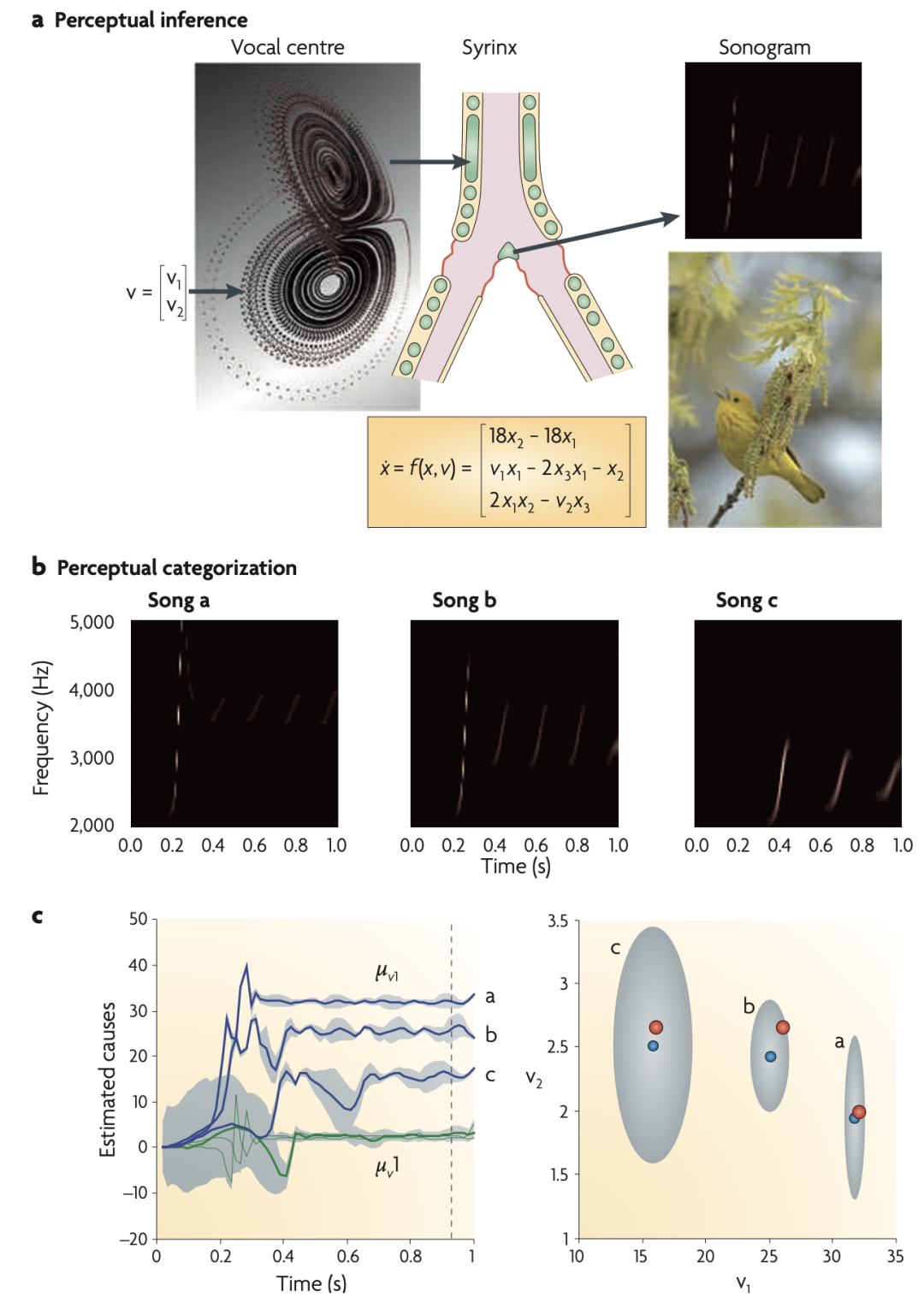
图 1：鸟鸣和感知分类。
（a）感知推理。用于模拟鸟类歌声的生成模型包含一个洛伦兹吸引子，它具有两个控制参数（或因果状态）（v（1）, v（2））。这些参数进而提供给一个合成的咽鼓管（syrinx），产生调制幅度和频率的“鸣叫声”（以声谱图形式展示）。然后将这些“鸣叫声”作为刺激呈现给一个合成鸟，测试它是否能够推断出潜在的因果状态，并对歌声进行分类。这包括通过改变控制参数的内部表征（μ（v1）, μ（v2））来最小化自由能。关于这个感知推理或分类的例子如下图所示。

（b）感知分类。这里展示的是三种模拟歌声的声谱图。每种歌声包括一系列鸣叫声，其频率和数量从歌曲a到歌曲c逐渐减少，因为一个因果状态（被称为瑞利数，Raleigh number，a中的v1）减少了。

（c）条件期望图和条件密度图。左图展示三首歌对应的因果状态的条件期望（μ（v1）, μ（v2）），作为刺激后时间的函数。图中显示，因果状态在大约600毫秒后被准确地识别出来（90%的置信区间以灰色显示）。右图显示在刺激后时间即将结束前的条件密度（即左图中的虚线）。蓝点对应条件期望，灰色区域对应90%的条件置信区域。注意，这些包括用于生成歌声的真实值（红点）（v（1）, v（2））。

这些结果说明在图2中推理方案下的感知分类的本质：这里，识别相当于将连续变化和混沌的感觉输入映射到感知空间中的一个固定点。

这种信息传递与真实大脑皮层层级中的功能不对称性是一致的[45]，其中前向连接（传递预测错误）是驱动性的，而后向连接（模拟感觉输入的非线性生成）同时具有驱动性和调节性[46]。这种不对称的信息传递也是自适应共振理论 [47,48] 的一个特征，它与预测编码在形式上有相似之处。

适应性共振理论（Adaptive Resonance Theory，简称ART）是一种关于大脑如何处理信息的神经网络理论。它由Stephen Grossberg 在20世纪70年代提出，主要描述大脑如何能够在稳定记忆旧信息的同时学习新信息，这一过程称为“适应性共振”。

总之，贝叶斯大脑和预测编码的基本主题是，大脑是一个推理引擎，它试图优化导致其感觉输入的概率表征。这种优化可以利用（变分自由能）“惊奇”约束来实现。简而言之，自由能原理包含了贝叶斯大脑假说，可以通过该领域的许多方案来实现。这些方案几乎无一例外地涉及到大脑区域或单元之间某种形式的信息传递或信念传播。这样，我们就可以将自由能原理与另一种感官处理原则方法，即信息论联系起来。

3. 高效编码原则

高效编码原则（principle of efficient coding）认为，大脑会在表征效率的约束条件下，优化感官与其内部表征之间的互信息（即相互可预测性，mutual predictability）。Barlow [49] 用减少冗余原则（redundancy reduction principle，或高效编码原则）阐述了这一思路，后来又用 infomax 原则 [50] 将其形式化。它已被应用于机器学习[51]和神经生物学 [53,54,55,56]，前者产生了独立成分分析（independent component analysis）[52]等方法，后者有助于理解神经元反应的本质。这一原理在预测经典感受野的经验特征方面极为有效[53]，并为稀疏编码[55]和视觉层次中处理流的分隔[57]提供了原理性解释。它还被扩展到动力学和运动轨迹[58,59]，甚至用于推断神经元处理过程中的代谢限制[60]。

简单来说，信息最大化原则（infomax principle）指出神经活动应该以一种高效和简约的方式编码感觉信息。它考虑的是一组变量（感觉状态）与另一组变量（表征这些状态的变量）之间的映射。乍一看，这似乎排除了概率表征，因为这将涉及感觉状态和概率密度之间的映射。然而，信息最大化原则可以应用于识别密度的充分统计量。当我们忽略概率表征中的不确定性（并且不考虑大脑如何通过行动去改变它接收的感觉信息时），信息最大化原则可以看作自由能原理的一个特殊情况（数学细节请参见补充信息 S3 框）。如果注意到感官信号是原因生成的，就很容易看到这一点。这意味着表征原因对于预测信号就是足够的。更形式化地，信息最大化原则可以理解为将自由能分解为复杂性和精确性：当条件期望最大化准确性（或最小化预测误差），并通过最小化复杂性确保效率时，互信息是最优化的。这确保没有过多的参数应用于生成模型，并导致一种符合其原因先验约束的简约感觉数据表征。有趣的是，更先进的模型优化技术使用自由能优化来消除多余的模型参数[61]，表明自由能优化可能为大脑在神经发育[62]和睡眠[63]期间发生的突触修剪和稳态调节提供一个很好的解释。

信息最大化原则关注如何将感觉输入高效地映射到神经表征上，而生成模型关注的是如何从原因映射回感觉输入，这两种视角如何协调呢？事实上，它们可以调和一致，因为基于信息最大化的所有识别方案都可以被视为在优化生成模型的参数[64]。例如，在稀疏编码模型中[55]，我们假设大脑认为感觉输入背后的原因是独立的，它们遵循重尾或稀疏分布[42]。这种模型非常擅长预测实验中观察到的神经元感受野的行为，这可能意味着我们的大脑被赋予（或习得）了先验预期，即我们感觉背后的原因通常是独立且稀疏的。

总之，高效编码原则认为大脑在优化感觉信号和简洁的神经表征之间的互信息。这与在复杂性约束下，优化生成模型的参数以增强预测的准确性是一致的。这两个过程都符合自由能原理的要求，它可以被视为信息最大化原则的一种概率扩展。我们接下来讨论关于大脑功能的更多生物启发的想法，聚焦于神经动力学和可塑性。这将让我们深入神经生物学机制，以及上文提到的原理的实现。

4. 细胞集群和相关性理论

细胞集群理论（cell assembly theory）由 Hebb[65]提出，并包含赫布可塑性或联想可塑性，这是使用依赖型或经验依赖型可塑性（experience-dependent plasticity）[66]、von de Malsburg 的相关性理论[67,68]以及对赫布可塑性本身的其他形式改进[69]的基础。细胞集群理论认为，成群神经元依赖于前突触和后突触的关联活动，通过增强的突触连接形成相互连接的网络，这意味着“一起放电的细胞会相互连接”（cells that fire together wire together）。这使得大脑能够从感官中提炼出统计规律。相关性理论（correlation theory）认为，同一物体的不同感知属性（例如，运动中的红色公共汽车）所引起的快速同步活动，可有选择性地提高突触效能及其可塑性（也称为再可塑性，metaplasticity[70]）。这解决了经典可塑性的一个缺陷，即无法将突触前输入归因于世界中的某个特定原因（例如红色）[67]。相关性理论是同步大脑活动及其在将属性关联或绑定到特定对象或原因上的作用的理论基础[68,71]。以联想可塑性为基础的另一个重要领域是使用吸引子网络作为记忆形成和检索的模型[72,73,74]。那么，相关性和联想可塑性在自由能公式中是如何体现的呢？

在之前的讨论中，我们主要关注了大脑如何对引起感觉信号的世界状态进行推断，其中关于状态的条件期望是通过突触活动编码的。然而，识别密度涵盖的原因不仅限于时变状态（例如，视觉场景中物体的运动），还包括赋予世界因果结构的时不变规律（例如，物体以恒定加速度下落）。这些规律是生成模型的参数，大脑需要对这些参数进行推断——换句话说，这些参数的条件期望值，它们可能通过突触效能被编码（在方框2中用μθ表示），需要被优化。这相当于优化大脑中的连接强度，即学习基础上的可塑性。那么，这种学习会采取什么形式呢？结果表明，自由能的梯度下降（即改变连接以减少自由能）在形式上与赫布式可塑性（Hebbian plasticity）相同[28,42]（方框 2）。这是因为生成模型的参数决定了预期状态（突触活动）如何混合以形成预测，简单地说，当突触前预测和突触后预测误差高度相关时，连接强度增加，使得预测能更有效地抑制预测误差。

简而言之，细胞集群的形成反映了因果规律的编码。这实际上是将细胞集群理论重新表述为自由能原理的一个特定实现（预测编码）。需要认识到，预测编码中的学习规则实际上是一种增量规则（delta rule），它依赖于赫布式机制；然而，赫布关于细胞集群的更广泛概念是从非统计角度提出的。现代的重新阐述表明，对状态的推断（即感知）和对参数的推断（即学习）都是为了最小化自由能（即最小化预测误差），并且是为了限制对世界的“惊奇”。那么，关于同步和突触的选择性启用又是怎么回事呢？

5. 有偏竞争和注意力

因果规律是通过突触效能来控制的，它决定了世界各种状态的确定性演化。但是，这些状态的随机涨落对于产生感觉数据也很关键。涨落幅度通常用精度（或者逆方差（inverse variance））来表示，反映了预测误差的可信度。精度在大脑处理信息的层次结构中非常重要，因为它决定了自下而上的预测误差与自上而下的预测在整个信息处理中的相对重要性。那么精度在大脑中是如何编码的呢？在预测编码中，精度调节预测误差的幅度（即方框 2 中的μ（γ）），即具有高精度的预测误差对编码条件期望的单元产生更大的影响。这实际上意味着，精度与预测误差单元的突触增益是对应的。调节这种增益的最明显方案是利用多巴胺和乙酰胆碱等经典神经调节剂，这为注意力和不确定性的理论提供了一个很好的链接[75,76,77]。另一种方案是快速同步的突触前输入，这种活动可以降低突触后膜的有效时间常数并提高同步增益[78]。这与相关性理论很好地契合，也跟大脑如何通过同步活动来调节注意力这些新想法有关[79,80]。

总之，从突触增益的角度优化预期精度将注意力与突触增益和同步联系起来。这种联系是注意力增益和有偏竞争理论[80,81,82,83,84,85]的核心，尤其是在神经调节[86,87]的背景下。尽管之前的讨论主要集中在感知上，然而，根据自由能原理，为了减少对环境的惊奇，大脑不仅需要处理感知数据，还需要通过行动来影响环境。在下一节中，我们将继续关注细胞集群，但将转向刺激-反应联系的选择和强化。

6. 神经达尔文主义与价值学习

神经元群体选择理论（theory of neuronal group selection）[88]从选择压力的角度考虑神经元集群的形成。这个理论包含四个要素：表观遗传机制创建神经连接的原初库，这些连接通过经验依赖的可塑性被完善，产生神经元群体的次级库。它们通过神经元群之间的重入信号（reentrant signaling）得到选择和维持。这与细胞集群理论相似，可塑性都依赖于突触前和突触后的关联活动，但这里它受到价值的调节。价值由递增（译注：从大脑较低区域向更高级的认知区域发送信号的神经传递路径）的神经调节递质系统发出信号，并控制哪些神经元群被选择，哪些不被选择。神经达尔文主义（neural Darwinism）的美妙之处在于，它将不同的选择过程彼此嵌套。换句话说，它避免了单一的选择单元，而利用元选择的概念（meta-selection，即选择选择机制；参见文献[89]）。在这个语境下，（神经元）的价值（value）通过选择介导适应性刺激-刺激关联和刺激-反应链接的神经元群体，来赋予演化价值（即适应度）。价值具备的这种能力是自然选择所保证的，因为神经元的价值系统本身也受到选择压力的影响。

重入信号（reentrant signaling）是一种神经科学中的概念，指的是神经元或神经元群体之间的双向通信模式。这种信号传递不仅单向从一个神经元传递到另一个，而是形成一个循环回路，使得信息可以在神经网络中来回流动。

这一理论，特别是依赖价值的学习（value-dependent learning）[90]，与强化学习及工程学中的相关方法，如动态规划（dynamic programming）和时序差分模型（temporal difference models）[91,92]有着密切的联系。这是因为神经价值系统强化了与自身的连接，这意味着大脑在评估一个感觉状态时，不仅考虑当前的价值，还考虑它是否能够导向另一个有价值的状态。这确保了智能体能够通过一系列获得价值的状态，以访问具有遗传指定的内在价值的状态（奖励）。简而言之，大脑会将价值最大化，这可能反映在价值系统（例如多巴胺能系统[92,93,94,95,96]）的放电上。那么，这与自由能的优化有什么关系呢？

答案很简单：价值与“惊奇”成反比，这意味着一个表型处于特定状态的概率随着该状态的价值增加而增加。进一步来说，一个表型的进化价值是其经历的所有状态的负“惊奇”的平均值，也就是其负熵。确实，最小化自由能（以及隐含的熵）的整个目的是确保智能体大部分时间都处于少数有价值的状态。这意味着自由能是价值的补充，其长期平均值是适应能力的补充（在进化生物学中也称为自由适应能力[97]）。但智能体如何知道什么是有价值的？换句话说，一代如何告诉下一代哪些状态有价值（即不令人“惊奇”）？价值或惊奇由智能体的生成模型及其隐含的先验决定——这些先验指定了感觉状态的价值，并且可以通过基因和表观遗传机制遗传。这意味着先验期望（即原初库）可以规定一小部分具有内在价值的吸引态。反过来，这使得自然选择能够优化先验期望，并确保它们与个体的表型一致。简而言之，有价值的状态就是智能体预期会频繁所处的状态。这些期望受其生成模型的形式约束，该模型由基因指定，并在主动推理框架下通过行为实现。

重要的是要认识到，先验预期不仅包括将从世界中采样什么，还包括如何采样世界。这就意味着，自然选择可能会给智能体带来一种先验预期，即智能体会一直探索环境，直到遇到具有先天价值的状态为止。在后续部分，我们将深入探讨这一点，特别是将状态空间的运动预设解释为强化学习中的策略。

神经达尔文主义和自由能原理都在探讨进化背景下个体生理变化的问题：神经达尔文主义关注的是选择过程，而自由能原理关注的是从熵和“惊奇”角度对集群或种群动力学的优化。这里出现的关键主题是，可遗传的先验期望能够将某些事物标记为天生有价值（即不令人惊奇的）；但简单地给状态贴标签如何能产生适应性行为呢？在下一部分，我们将重新聚焦于强化学习及相关的行动公式，这些公式试图仅通过标签或成本函数来解释适应性行为。

7. 最优控制理论和博弈论

价值（value）是基于强化学习和最优控制理论的大脑功能理论的核心。这些理论的基本观念是大脑优化价值，这里价值被理解为预期的奖励或效用（或者相对应的，预期的损失或成本）。在行为心理学领域，这被称为强化学习[98]；在计算神经科学和机器学习领域，这体现为动态规划的变体，如时序差分学习[99,100,101]；而在经济学中，则体现为期望效用理论[102]。预期奖励或成本（cost）的概念是这里的关键，它代表了在给定行动或选择策略的情况下对未来状态的预期成本。策略指定了智能体将从任何给定状态移动到哪些状态（“在连续时间内通过状态空间的运动”）。这一策略必须使用成本函数来访问稀疏的奖励状态，该函数仅将状态标记为有成本或无成本。策略如何优化的问题在最优控制理论中被形式化为贝尔曼方程及其变体[99]（见补充信息 S4 方框），这些方程以最优策略和成本函数为基础表达价值。如果能求解贝尔曼方程，就可以将每个感觉状态与一个价值关联起来，并通过确保下一个状态是可用状态中最有价值的来优化策略。通常，贝尔曼方程无法精确求解，但存在多种近似方法，从简单的 Rescorla-Wagner 模型[98]到更全面的公式化方法如 Q-learning[100]。成本在贝叶斯决策理论中也扮演关键角色，其中最优决策在关于结果的不确定性背景下最小化预期成本；这是最优决策理论（博弈论）和行为经济学的核心[102,103,104]。

自由能在这里的作用是什么呢？假设最优策略是通过增加价值的梯度来实现的，那么我们可以清楚地看到价值与“惊奇”是成反比的（见补充信息 S4 方框）。这表明自由能是预期成本的上限，这与最优控制理论相符，后者假定行动是为了最小化预期成本，而自由能原理则指出目的是最小化自由能。这一点至关重要，因为它阐明了智能体为什么需要最小化预期成本。此外，自由能还为强化学习中的成本函数与进化生物学中的价值之间建立了定量和无缝的联系。最后，从动力学的角度看，自由能原理为大脑如何确定行为策略提供了机制性的理解：根据最优性原理 [99]，成本是价值随时间变化的速率（见补充信息 S4 方框），这取决于感觉状态的变化。这意味着最优策略可以由对感觉状态变化的先验期望来定义。简而言之，先验设定了一个固定点吸引子，当状态达到这一固定点时，价值将保持不变，成本达到最小。图2中展示了一个简单示例，这里的手臂运动仅使用先验期望——手臂将被吸引至一个固定点（目标）——来模拟。图中展示了计算运动控制如何可以用先验和抑制感觉预测误差来实现 [105,106,107,108,109]。从更广泛的角度来看，它展示了如何将奖励和目标理解为行为必须遵循的先验期望 [16]（另见参考文献 110）。它还表明，自然选择如何通过可继承或先天性先验条件的遗传特化来优化行为，从而限制经验先验（方框2）的学习，及随后的目标导向行为。

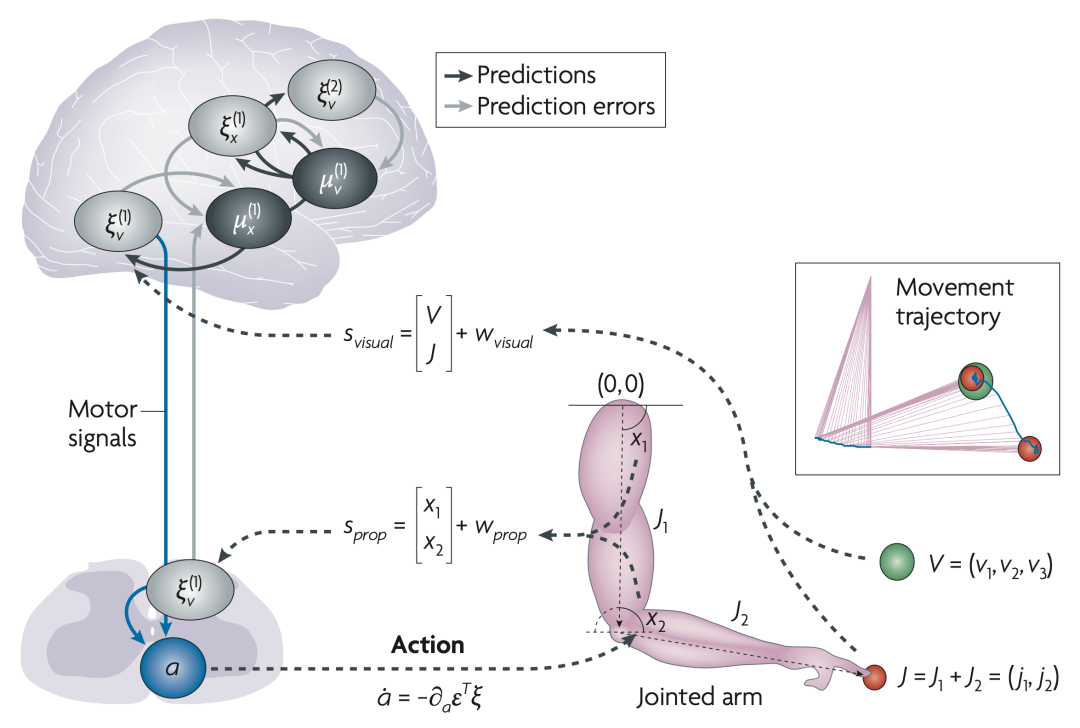
图2. 提示性伸手动作示例。图的右下部分显示一个马达装置，包括具有两个隐藏状态的双关节臂，每个隐藏状态对应于两个关节的特定角度位置。食指的当前位置（红色圆圈）是描述每个关节位置的向量之和。这里世界的因果状态是目标的位置和亮度（绿色圆圈）。图的左侧部分说明大脑使用称为本体感觉输入（Sprop，信号传递关节的角度位置（x1，x2））的方式直接感知隐藏状态，并通过观察手指在空间中的位置（J1，J2）间接感知。此外，通过视觉输入（Svisual），智能体感知目标的位置（v1，v2）和亮度（v3）。感觉预测误差传递到大脑的更高层，以优化隐藏状态（即关节的角度位置）和因果状态（即目标）的条件期望。随后的预测被发送回来抑制感觉预测误差。与此同时，感觉预测误差还试图通过行动改变感觉输入来抑制自己。

灰色和黑色的线表示编码预测误差和条件期望的神经元群体之间的相互传递信息；这种架构与方框2中所示的相同。蓝色的线代表来自感觉预测误差单元的下行运动控制信号。智能体的生成模型包括对隐藏状态运动的先验，有效地在手指和目标之间形成一个看不见的弹性带（当目标被照亮时）。这产生了一个先验期望，即在适当的提示下，手指会被吸引到目标上。插图显示了由动作引起的运动轨迹。红色圆圈表示手指的初始和最终位置，它迅速而平稳地到达目标（绿色圆圈）；蓝线是模拟的轨迹。

仅仅期望被吸引到某些状态可能还不足以实现达到这些状态的目标。因为实现这些目标状态可能需要间接地通过其他状态来接近吸引子（例如，为了避开障碍物），或者需要遵守行动的物理约束。这些问题是强化学习和最优控制需要解决的一些更为复杂的问题，它们涉及如何获取远程奖励。在这种情况下，基于自由能原理分析密度动力学（density dynamics）表明，只需保持运动直到遇到先验吸引子即可（见补充信息 S5 方框）。这就需要破坏环境中意想不到的（代价高昂的）固定点，使其变得不稳定（就像坐得不舒服时换个姿势）。从数学上讲，这意味着要采取一种策略，确保代价高昂的状态出现正发散（直观地说，这就像被推着穿过具有负粘度或摩擦力的液体一样）。图3是经典山地车问题的一个解决方案，使用一个简单的先验来诱导这种策略。这个先验是关于在状态空间中的运动（即状态的变化），并强制探索直到找到一个吸引态。这种先验可以为理解探索-利用权衡 [111,112,113] 以及进化生物学中的相关问题[114]提供一种原则性的方法。隐含使用先验来诱导动态不稳定性，也是与大脑动力系统理论方法的重要联系，后者强调巡游动力学（itinerant dynamics）、亚稳态、自组织临界性和无赢家竞争（winner-less competition）的重要性 [115,116,117,118,119,120,121,122,123]。这些动力学现象在自适应行为的协同和自创生描述中起着关键作用 [5,124,125]。

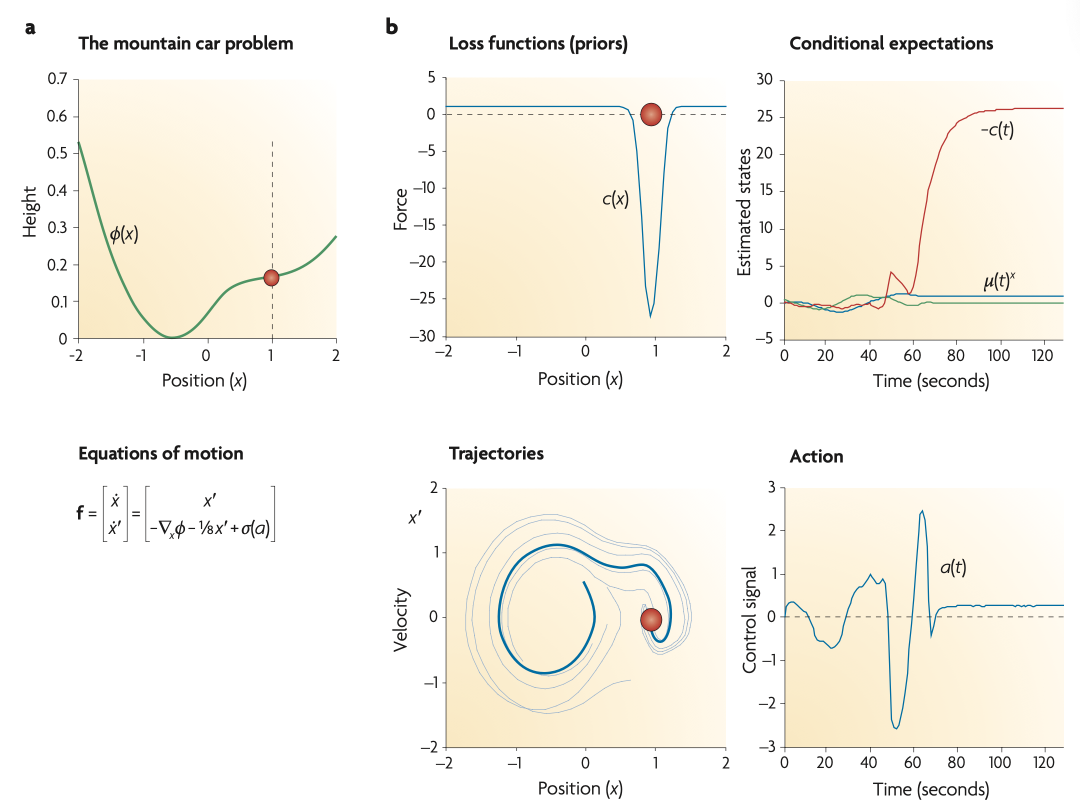
图3. 利用先验期望解决山地车问题。（a）如何从关于世界隐藏状态运动的简单先验中产生矛盾但适应性的行为（例如，远离目标以确保稍后获得安全）？图中显示的是山地车的势能函数或景观（在位置 x=–0.5 处取最小值）。山地车位于山坡上的目标位置 x=1，由红色圆圈标示。关键是，在 x=0 处，智能体无法克服对车辆的力，因为作用力被施加了一个压缩函数 –1≤σ≤1，以防止其大于1。这意味着智能体只能通过从左侧山坡中间开始获得足够的动力来到达另一侧的目标位置。

（b）先验条件下的主动推理结果破坏了目标域之外的固定点。先验条件编码在成本函数c（x）中（左上角），其表现类似于负摩擦。当“摩擦”为负时，车辆预期会更快地行驶（详见附录S5方框）。推断出的隐藏状态（右上角：蓝色表示位置，绿色表示速度，红色表示负耗散）显示车辆在探索其景观直到遇到目标，然后摩擦增加（即成本减少），以防止车辆逃离目标（滚下山坡）。随后的轨迹用蓝色表示（左下角）。较浅的线条展示了其他试验的示例轨迹，起始位置不同。在现实世界中，摩擦是恒定的。然而，车辆“预期”随着位置的变化而改变摩擦，从而强制进行探索或利用。这些期望通过行动得以实现（右下角）。

简而言之，最优控制和决策（博弈）理论以成本或效用为出发点，尝试构建状态的价值函数来引导行动。而自由能框架以对状态价值的自由能约束为基础，由隐藏的环境状态运动的先验假设定义。这些先验可以整合任何成本函数，以确保避开高成本的状态。最小成本的状态可以通过关于运动的先验期望以及随后形成的吸引子（通过学习或演化）来设定。这种观点认为，在环境中寻找稀缺奖励的挑战，实际上是自然界对如何最小化智能体状态熵（即平均“惊奇”或自由能）的解决方案：确保它们占据一组吸引（即，有奖励的）状态。

8. 结论和未来方向

尽管本综述构建了一个特定框架来突出共性，但它表明许多全局的大脑功能理论可以在亥姆霍兹视角下统一起来，将大脑视为它所处世界的生成模型[18,20,21,25]（图 4）。值得注意的例子包括贝叶斯大脑和计算运动控制理论的整合，预测编码和信息最大化原则共享的目标函数，层次推理和注意力理论，将感知嵌入自然选择中，以及最优控制与动力系统理论中更多奇特现象之间的联系。这些理论的共同主题是大脑优化对“惊奇”或其互补物（即价值）的（自由能）上界。这表现为感知（为了改变预测）或行动（为了改变预测到的感觉）。关键是，这些预测依赖于先验期望（提供策略），这些期望在不同（个体和进化）时间尺度上被优化，并定义了什么是有价值的。

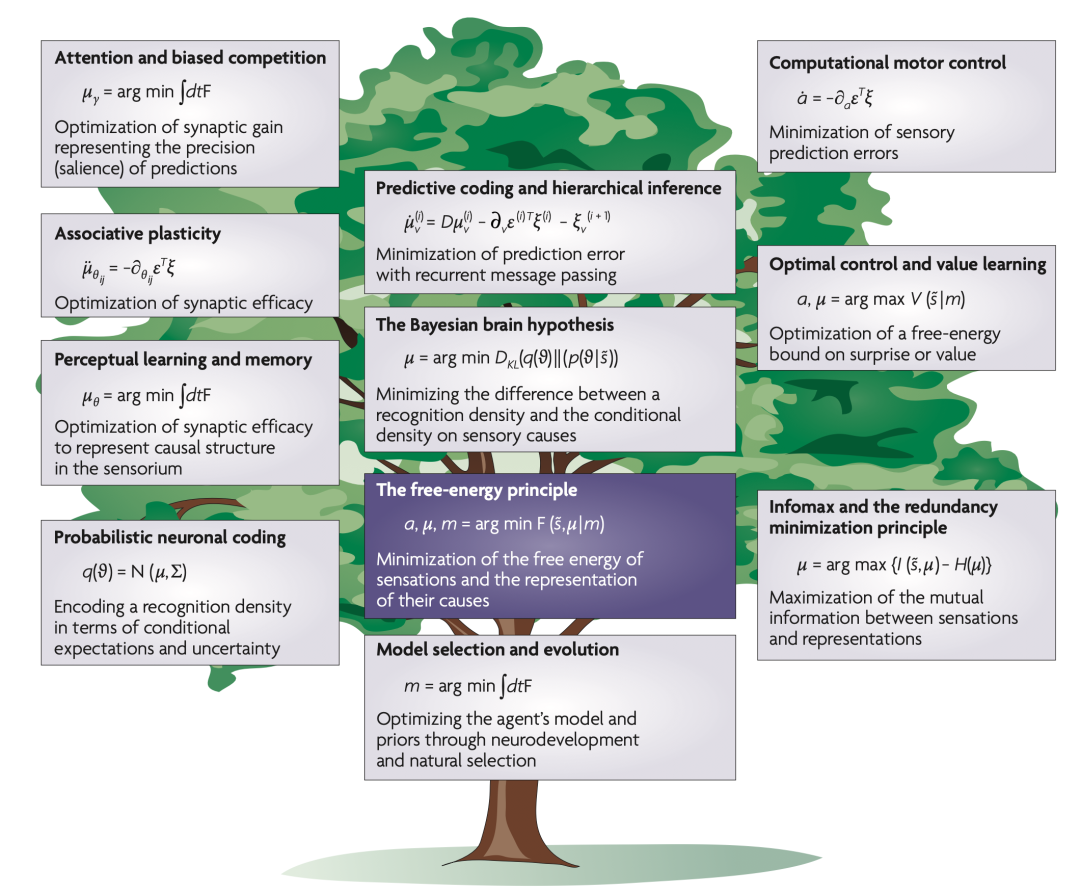
图4. 自由能原理及其他理论。这篇综述中考虑了一些理论构建，并阐述了它们与自由能原理的关系。变量的描述在第方框1、2中，方程的详细解释可以在补充信息S1–S4（方框）中找到。

自由能原理对未来有何预示？如果它的主要贡献是整合已有理论，那么答案可能是“不多”。相反，它可能提供了一个框架，在其中，当前的争论可能得到解决，例如多巴胺是编码奖励预测误差还是“惊奇”[126,127]——这对于理解像成瘾、帕金森病和精神分裂症等状况特别重要。事实上，自由能理论已被用于从错误推理的角度解释精神分裂症的症状[128]。自由能理论还可能为旧问题提供新方法，可能需要重新评估传统观念，特别是在强化学习和运动控制领域。

如果支撑自由能原理的论点成立，那么真正的挑战就是了解它在大脑中的表现形式。这就需要更深入地了解分层信息传递[41]，特定神经元和微电路的功能作用以及它们所支持的动力学（例如，大脑中的预测编码、注意力和动态协调之间的关系是什么？[129]）。除神经科学外，工程学、机器人学、具身认知和进化生物学等领域也有许多令人兴奋的应用；尽管是异想天开，但不难想象，我们可以构建小型自由能机器，它们可以收集感官信息并建立模型（就像孩子一样），从而最大限度地证明自己的存在。

自由能（Free energy）：一种信息论度量，在给定生成模型的情况下，对采样某些数据时的惊奇（surprise）设置了界限或限制（大于惊奇）。

稳态（Homeostasis）：一个开放或封闭系统调节其内部环境以维持其状态在一定范围内的过程。

熵（Entropy）：从概率分布或密度采样所得结果的平均惊奇度。熵低的密度意味着，平均而言，结果相对可预测。因此，熵是一种不确定性的度量。

涨落定理（Fluctuation theorem）：描述远离热力学平衡状态的系统中，熵在一定时间内增加或减少的概率。这个定理提供了一个框架，用于理解在非平衡条件下系统熵变化的规律性和可能性。

惊奇（Surprise）：一个结果的负对数概率。因此，不可能的结果（例如，水向上流）是令人惊奇的。

吸引子（Attractor）：一个动力系统经过足够长时间演化后所趋向的集合。接近吸引子的点即使在小的扰动下也保持接近。

Kullback-Leibler散度（Kullback-Leibler divergence）：两个概率分布之间非负差异的非交换度量。

识别密度（Recognition density）：数据（例如，感觉输入）原因的近似概率分布。它是推断或生成模型求逆的结果。

参考文献

Huang, G. Is this a unified theory of the brain?New Scientist 2658, 30–33（2008）.

Friston K., Kilner, J. & Harrison, L. A free energy principle for the brain. J. Physiol. Paris 100, 70–87（2006）.An overview of the free-energy principle that describes its motivation and relationship to generative models and predictive coding. This paper focuses on perception and the neurobiological infrastructures involved.

Ashby, W. R. Principles of the self-organising dynamic system. J. Gen. Psychol. 37, 125–128（1947）.

Nicolis, G. & Prigogine, I. Self‑Organisation in Non‑ Equilibrium Systems（Wiley, New York, 1977）.

Haken, H. Synergistics：an Introduction. Non‑ Equilibrium Phase Transition and Self‑Organisation in Physics, Chemistry and Biology 3rd edn（Springer, New York, 1983）.

Kauffman, S. The Origins of Order：Self‑Organization and Selection in Evolution（Oxford Univ. Press, Oxford, 1993）.

Bernard, C. Lectures on the Phenomena Common to Animals and Plants（Thomas, Springfield, 1974）.

Applebaum, D. Probability and Information：an Integrated Approach（Cambridge Univ. Press, Cambridge, UK, 2008）.

Evans, D. J. A non-equilibrium free energy theorem for deterministic systems. Mol. Physics 101, 15551–11554（2003）.

Crauel, H. & Flandoli, F. Attractors for random dynamical systems. Probab. Theory Relat. Fields 100, 365–393（1994）.

Feynman, R. P. Statistical Mechanics：a Set of Lectures（Benjamin, Reading, Massachusetts, 1972）.

Hinton, G. E. & von Cramp, D. Keeping neural networks simple by minimising the description length of weights. Proc. 6th Annu. ACM Conf. Computational Learning Theory 5–13（1993）.

MacKay. D. J. C. Free-energy minimisation algorithm for decoding and cryptoanalysis. Electron. Lett. 31, 445–447（1995）.

Neal, R. M. & Hinton, G. E. in Learning in Graphical Models（ed. Jordan, M. I.）355–368（Kluwer Academic, Dordrecht, 1998）.

Itti, L. & Baldi, P. Bayesian surprise attracts human attention. Vision Res. 49, 1295–1306（2009）.

Friston, K., Daunizeau, J. & Kiebel, S. Active inference or reinforcement learning? PLoS ONE 4, e6421（2009）.

Knill, D. C. & Pouget, A. The Bayesian brain：the role of uncertainty in neural coding and computation. Trends Neurosci. 27, 712–719（2004）.A nice review of Bayesian theories of perception and sensorimotor control. Its focus is on Bayes optimality in the brain and the implicit nature of neuronal representations.

von Helmholtz, H. in Treatise on Physiological Optics Vol. III 3rd edn（Voss, Hamburg, 1909）.

MacKay, D. M. in Automata Studies（eds Shannon, C. E. & McCarthy, J.）235–251（Princeton Univ. Press, Princeton, 1956）.

Neisser, U. Cognitive Psychology（Appleton-Century-Crofts, New York, 1967）.

Gregory, R. L. Perceptual illusions and brain models. Proc. R. Soc. Lond. B Biol. Sci. 171, 179–196（1968）.

Gregory, R. L. Perceptions as hypotheses. Philos. Trans. R. Soc. Lond. B Biol. Sci. 290, 181–197（1980）.

Ballard, D. H., Hinton, G. E. & Sejnowski, T. J. Parallel visual computation. Nature 306, 21–26（1983）.

Kawato, M., Hayakawa, H. & Inui, T. A forward-inverse optics model of reciprocal connections between visual areas. Network：Computation in Neural Systems 4, 415–422（1993）.

Dayan, P., Hinton, G. E. & Neal, R. M. The Helmholtz machine. Neural Comput. 7, 889–904（1995）. This paper introduces the central role of generative models and variational approaches to hierarchical self-supervised learning and relates this to the function of bottom-up and top-down cortical processing pathways.

Lee, T. S. & Mumford, D. Hierarchical Bayesian inference in the visual cortex. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 20, 1434–1448（2003）.

Kersten, D., Mamassian, P. & Yuille, A. Object perception as Bayesian inference. Annu. Rev. Psychol. 55, 271–304（2004）.

Friston, K. J. A theory of cortical responses. Philos. Trans. R. Soc. Lond. B Biol. Sci. 360, 815–836（2005）.

Beal, M. J. Variational Algorithms for Approximate Bayesian Inference. Thesis, University College London（2003）.

Efron, B. & Morris, C. Stein’s estimation rule and its competitors – an empirical Bayes approach. J. Am. Stats. Assoc. 68, 117–130（1973）.

Kass, R. E. & Steffey, D. Approximate Bayesian inference in conditionally independent hierarchical models（parametric empirical Bayes models）. J. Am. Stat. Assoc. 407, 717–726（1989）.

Zeki, S. & Shipp, S. The functional logic of cortical connections. Nature 335, 311–317（1988）. Describes the functional architecture of cortical hierarchies with a focus on patterns of anatomical connections in the visual cortex. It emphasizes the role of functional segregation and integration（that is, message passing among cortical areas）.

Felleman, D. J. & Van Essen, D. C. Distributed hierarchical processing in the primate cerebral cortex. Cereb. Cortex 1, 1–47（1991）.

Mesulam, M. M. From sensation to cognition. Brain 121, 1013–1052（1998）.

Sanger, T. Probability density estimation for the interpretation of neural population codes. J. Neurophysiol. 76, 2790–2793（1996）.

Zemel, R., Dayan, P. & Pouget, A. Probabilistic interpretation of population code. Neural Comput. 10, 403–430（1998）.

Paulin, M. G. Evolution of the cerebellum as a neuronal machine for Bayesian state estimation. J. Neural Eng. 2, S219–S234（2005）.

Ma, W. J., Beck, J. M., Latham, P. E. & Pouget, A. Bayesian inference with probabilistic population codes. Nature Neurosci. 9, 1432–1438（2006）.

Friston, K., Mattout, J., Trujillo-Barreto, N., Ashburner, J. & Penny, W. Variational free energy and the Laplace approximation. Neuroimage 34, 220–234（2007）.

Rao, R. P. & Ballard, D. H. Predictive coding in the visual cortex：a functional interpretation of some extra-classical receptive field effects. Nature Neurosci. 2, 79–87（1998）.Applies predictive coding to cortical processing to provide a compelling account of extra-classical receptive fields in the visual system. It emphasizes the importance of top-down projections in providing predictions, by modelling perceptual inference.

Mumford, D. On the computational architecture of the neocortex. II. The role of cortico-cortical loops. Biol. Cybern. 66, 241–251（1992）.

Friston, K. Hierarchical models in the brain. PLoS Comput. Biol. 4, e1000211（2008）.

Murray, S. O., Kersten, D., Olshausen, B. A., Schrater, P. & Woods, D. L. Shape perception reduces activity in human primary visual cortex. Proc. Natl Acad. Sci. USA 99, 15164–15169（2002）.

Garrido, M. I., Kilner, J. M., Kiebel, S. J. & Friston,K. J. Dynamic causal modeling of the response to frequency deviants. J. Neurophysiol. 101, 2620–2631（2009）.

Sherman, S. M. & Guillery, R. W. On the actions that one nerve cell can have on another：distinguishing “drivers” from “modulators”. Proc. Natl Acad. Sci. USA 95, 7121–7126（1998）.

Angelucci, A. & Bressloff, P. C. Contribution of feedforward, lateral and feedback connections to the classical receptive field center and extra-classical receptive field surround of primate V1 neurons. Prog. Brain Res. 154, 93–120（2006）.

Grossberg, S. Towards a unified theory of neocortex：laminar cortical circuits for vision and cognition. Prog. Brain Res. 165, 79–104（2007）.

Grossberg, S. & Versace, M. Spikes, synchrony, and attentive learning by laminar thalamocortical circuits. Brain Res. 1218, 278–312（2008）.

Barlow, H. in Sensory Communication（ed. Rosenblith, W.）217–234（MIT Press, Cambridge, Massachusetts, 1961）.

Linsker, R. Perceptual neural organisation：some approaches based on network models and information theory. Annu. Rev. Neurosci. 13, 257–281（1990）.

Oja, E. Neural networks, principal components, and subspaces. Int. J. Neural Syst. 1, 61–68（1989）.

Bell, A. J. & Sejnowski, T. J. An information maximisation approach to blind separation and blind de-convolution. Neural Comput. 7, 1129–1159（1995）.

Atick, J. J. & Redlich, A. N. What does the retina know about natural scenes? Neural Comput. 4, 196–210（1992）.

Optican, L. & Richmond, B. J. Temporal encoding of two-dimensional patterns by single units in primate inferior cortex. III Information theoretic analysis.J. Neurophysiol. 57, 132–146（1987）.

Olshausen, B. A. & Field, D. J. Emergence of simple- cell receptive field properties by learning a sparse code for natural images. Nature 381, 607–609（1996）.

Simoncelli, E. P. & Olshausen, B. A. Natural image statistics and neural representation. Annu. Rev. Neurosci. 24, 1193–1216（2001）.A nice review of information theory in visual processing. It covers natural scene statistics and empirical tests of the efficient coding hypothesis in individual neurons and populations of neurons.

Friston, K. J. The labile brain. III. Transients and spatio-temporal receptive fields. Philos. Trans. R. Soc. Lond. B Biol. Sci. 355, 253–265（2000）.

Bialek, W., Nemenman, I. & Tishby, N. Predictability, complexity, and learning. Neural Comput. 13, 2409–2463（2001）.

Lewen, G. D., Bialek, W. & de Ruyter van Steveninck,R. R. Neural coding of naturalistic motion stimuli.Network 12, 317–329（2001）.

Laughlin, S. B. Efficiency and complexity in neural coding. Novartis Found. Symp. 239, 177–187（2001）.

Tipping, M. E. Sparse Bayesian learning and the Relevance Vector Machine. J. Machine Learn. Res. 1, 211–244（2001）.

Paus, T., Keshavan, M. & Giedd, J. N. Why do many psychiatric disorders emerge during adolescence? Nature Rev. Neurosci. 9, 947–957（2008）.

Gilestro, G. F., Tononi, G. & Cirelli, C. Widespread changes in synaptic markers as a function of sleep and wakefulness in Drosophila. Science 324, 109–112（2009）.

Roweis, S. & Ghahramani, Z. A unifying review of linear Gaussian models. Neural Comput. 11, 305–345（1999）.

Hebb, D. O. The Organization of Behaviour（Wiley, New York, 1949）.

Paulsen, O. & Sejnowski, T. J. Natural patterns of activity and long-term synaptic plasticity. Curr. Opin. Neurobiol. 10, 172–179（2000）.

von der Malsburg, C. The Correlation Theory of Brain Function. Internal Report 81–82, Dept. Neurobiology, Max-Planck-Institute for Biophysical Chemistry（1981）.

Singer, W. & Gray, C. M. Visual feature integration and the temporal correlation hypothesis. Annu. Rev. Neurosci. 18, 555–586（1995）.

Bienenstock, E. L., Cooper, L. N. & Munro, P. W. Theory for the development of neuron selectivity：orientation specificity and binocular interaction in visual cortex. J. Neurosci. 2, 32–48（1982）.

Abraham, W. C. & Bear, M. F. Metaplasticity：the plasticity of synaptic plasticity. Trends Neurosci. 19, 126–130（1996）.

Pareti, G. & De Palma, A. Does the brain oscillate? The dispute on neuronal synchronization. Neurol. Sci. 25, 41–47（2004）.

Leutgeb, S., Leutgeb, J. K., Moser, M. B. & Moser, E. I. Place cells, spatial maps and the population code for memory. Curr. Opin. Neurobiol. 15, 738–746（2005）.

Durstewitz, D. & Seamans, J. K. Beyond bistability：biophysics and temporal dynamics of working memory. Neuroscience 139, 119–133（2006）.

Anishchenko, A. & Treves, A. Autoassociative memory retrieval and spontaneous activity bumps in small- world networks of integrate-and-fire neurons.J. Physiol. Paris 100, 225–236（2006）.

Abbott, L. F., Varela, J. A., Sen, K. & Nelson, S. B. Synaptic depression and cortical gain control. Science 275, 220–224（1997）.

Yu, A. J. & Dayan, P. Uncertainty, neuromodulation and attention. Neuron 46, 681–692（2005）.

Doya, K. Metalearning and neuromodulation. Neural Netw. 15, 495–506（2002）.

Chawla, D., Lumer, E. D. & Friston, K. J. The relationship between synchronization among neuronal populations and their mean activity levels. Neural Comput. 11, 1389–1411（1999）.

Fries, P., Womelsdorf, T., Oostenveld, R. & Desimone, R. The effects of visual stimulation and selective visual attention on rhythmic neuronal synchronization in macaque area V4. J. Neurosci. 28, 4823–4835（2008）.

Womelsdorf, T. & Fries, P. Neuronal coherence during selective attentional processing and sensory-motor integration. J. Physiol. Paris 100, 182–193（2006）.

Desimone, R. Neural mechanisms for visual memory and their role in attention. Proc. Natl Acad. Sci. USA 93, 13494–13499（1996）.A nice review of mnemonic effects（such as repetition suppression）on neuronal responses and how they bias the competitive interactions between stimulus representations in the cortex. It provides a good perspective on attentional mechanisms in the visual system that is empirically grounded.

Treisman, A. Feature binding, attention and object perception. Philos. Trans. R. Soc. Lond. B Biol. Sci. 353, 1295–1306（1998）.

Maunsell, J. H. & Treue, S. Feature-based attention in visual cortex. Trends Neurosci. 29, 317–322（2006）.

Spratling, M. W. Predictive-coding as a model of biased competition in visual attention. Vision Res. 48, 1391–1408（2008）.

Reynolds, J. H. & Heeger, D. J. The normalization model of attention. Neuron 61, 168–185（2009）.

Schroeder, C. E., Mehta, A. D. & Foxe, J. J. Determinants and mechanisms of attentional modulation of neural processing. Front. Biosci. 6, D672–D684（2001）.

Hirayama, J., Yoshimoto, J. & Ishii, S. Bayesian representation learning in the cortex regulated by acetylcholine. Neural Netw. 17, 1391–1400（2004）.

Edelman, G. M. Neural Darwinism：selection and reentrant signaling in higher brain function. Neuron 10, 115–125（1993）.

Knobloch, F. Altruism and the hypothesis of meta- selection in human evolution. J. Am. Acad. Psychoanal. 29, 339–354（2001）.

Friston, K. J., Tononi, G., Reeke, G. N. Jr, Sporns, O. & Edelman, G. M. Value-dependent selection in the brain：simulation in a synthetic neural model. Neuroscience 59, 229–243（1994）.

Sutton, R. S. & Barto, A. G. Toward a modern theory of adaptive networks：expectation and prediction. Psychol. Rev. 88, 135–170（1981）.

Montague, P. R., Dayan, P., Person, C. & Sejnowski,T. J. Bee foraging in uncertain environments using predictive Hebbian learning. Nature 377, 725–728（1995）.A computational treatment of behaviour that combines ideas from optimal control theory and dynamic programming with the neurobiology of reward. This provided an early example of value learning in the brain.

Schultz, W. Predictive reward signal of dopamine neurons. J. Neurophysiol. 80, 1–27（1998）.

Daw, N. D. & Doya, K. The computational neurobiology of learning and reward. Curr. Opin. Neurobiol. 16, 199–204（2006）.

Redgrave, P. & Gurney, K. The short-latency dopamine signal：a role in discovering novel actions? Nature Rev. Neurosci. 7, 967–975（2006）.

Berridge, K. C. The debate over dopamine’s role in reward：the case for incentive salience. Psychopharmacology（Berl.）191, 391–431（2007）.

Sella, G. & Hirsh, A. E. The application of statistical physics to evolutionary biology. Proc. Natl Acad. Sci. USA 102, 9541–9546（2005）.

Rescorla, R. A. & Wagner, A. R. in Classical Conditioning II：Current Research and Theory（eds Black, A. H. & Prokasy, W. F.）64–99（Appleton Century Crofts, New York, 1972）.

Bellman, R. On the Theory of Dynamic Programming.Proc. Natl Acad. Sci. USA 38, 716–719（1952）.

Watkins, C. J. C. H. & Dayan, P. Q-learning. Mach. Learn. 8, 279–292（1992）.

Todorov, E. in Advances in Neural Information Processing Systems（eds Scholkopf, B., Platt, J. & Hofmann T.）19, 1369–1376（MIT Press, 2006）.

Camerer, C. F. Behavioural studies of strategic thinking in games. Trends Cogn. Sci. 7, 225–231（2003）.

Smith, J. M. & Price, G. R. The logic of animal conflict.Nature 246, 15–18（1973）.

Nash, J. Equilibrium points in n-person games.Proc. Natl Acad. Sci. USA 36, 48–49（1950）.

Wolpert, D. M. & Miall, R. C. Forward models for physiological motor control. Neural Netw. 9, 1265–1279（1996）.

Todorov, E. & Jordan, M. I. Smoothness maximization along a predefined path accurately predicts the speed profiles of complex arm movements. J. Neurophysiol. 80, 696–714（1998）.

Tseng, Y. W., Diedrichsen, J., Krakauer, J. W., Shadmehr, R. & Bastian, A. J. Sensory prediction- errors drive cerebellum-dependent adaptation of reaching. J. Neurophysiol. 98, 54–62（2007）.

Bays, P. M. & Wolpert, D. M. Computational principles of sensorimotor control that minimize uncertainty and variability. J. Physiol. 578, 387–396（2007）.A nice overview of computational principles in motor control. Its focus is on representing uncertainty and optimal estimation when extracting the sensory information required for motor planning.

Shadmehr, R. & Krakauer, J. W. A computational neuroanatomy for motor control. Exp. Brain Res. 185, 359–381（2008）.

Verschure, P. F., Voegtlin, T. & Douglas, R. J. Environmentally mediated synergy between perception and behaviour in mobile robots. Nature 425, 620–624（2003）.

Cohen, J. D., McClure, S. M. & Yu, A. J. Should I stay or should I go? How the human brain manages the trade-off between exploitation and exploration. Philos. Trans. R. Soc. Lond. B Biol. Sci. 362, 933–942（2007）.

Ishii, S., Yoshida, W. & Yoshimoto, J. Control of exploitation-exploration meta-parameter in reinforcement learning. Neural Netw. 15, 665–687（2002）.

Usher, M., Cohen, J. D., Servan-Schreiber, D., Rajkowski, J. & Aston-Jones, G. The role of locus coeruleus in the regulation of cognitive performance. Science 283, 549–554（1999）.

Voigt, C. A., Kauffman, S. & Wang, Z. G. Rational evolutionary design：the theory of in vitro protein evolution. Adv. Protein Chem. 55, 79–160（2000）.

Freeman, W. J. Characterization of state transitions in spatially distributed, chaotic, nonlinear, dynamical systems in cerebral cortex. Integr. Physiol. Behav. Sci. 29, 294–306（1994）.

Tsuda, I. Toward an interpretation of dynamic neural activity in terms of chaotic dynamical systems. Behav. Brain Sci. 24, 793–810（2001）.

Jirsa, V. K., Friedrich, R., Haken, H. & Kelso, J. A.A theoretical model of phase transitions in the human brain. Biol. Cybern. 71, 27–35（1994）.This paper develops a theoretical model（based on synergetics and nonlinear oscillator theory）that reproduces observed dynamics and suggests a formulation of biophysical coupling among brain systems.

Breakspear, M. & Stam, C. J. Dynamics of aneural system with a multiscale architecture. Philos. Trans. R. Soc. Lond. B Biol. Sci. 360, 1051–1074（2005）.

Bressler, S. L. & Tognoli, E. Operational principles of neurocognitive networks. Int. J. Psychophysiol. 60, 139–148（2006）.

Werner, G. Brain dynamics across levels of organization. J. Physiol. Paris 101, 273–279（2007）.

Pasquale, V., Massobrio, P., Bologna, L. L., Chiappalone, M. & Martinoia, S. Self-organization and neuronal avalanches in networks of dissociated cortical neurons. Neuroscience 153, 1354–1369（2008）.

Kitzbichler, M. G., Smith, M. L., Christensen, S. R. & Bullmore, E. Broadband criticality of human brain network synchronization. PLoS Comput. Biol. 5, e1000314（2009）.

Rabinovich, M., Huerta, R. & Laurent, G. Transient dynamics for neural processing. Science 321 48–50（2008）.

Tschacher, W. & Hake, H. Intentionality in non- equilibrium systems? The functional aspects of self- organised pattern formation. New Ideas Psychol. 25, 1–15（2007）.

Maturana, H. R. & Varela, F. De máquinas y seres vivos（Editorial Universitaria, Santiago, 1972）. English translation available in Maturana, H. R. & Varela, F. in Autopoiesis and Cognition（Reidel, Dordrecht, 1980）.

Fiorillo, C. D., Tobler, P. N. & Schultz, W. Discrete coding of reward probability and uncertainty by dopamine neurons. Science 299, 1898–1902（2003）.

Niv, Y., Duff, M. O. & Dayan, P. Dopamine, uncertainty and TD learning. Behav. Brain Funct. 1, 6（2005）.

Fletcher, P. C. & Frith, C. D. Perceiving is believing：a Bayesian approach to explaining the positive symptoms of schizophrenia. Nature Rev. Neurosci. 10, 48–58（2009）.

Phillips, W. A. & Silverstein, S. M. Convergence of biological and psychological perspectives on cognitive coordination in schizophrenia. Behav. Brain Sci. 26, 65–82（2003）.

Friston, K. & Kiebel, S. Cortical circuits for perceptual inference. Neural Netw. 22, 1093–1104（2009）.