无论是生活还是在数学的世界里，我们常常会陷入某些既定的思维模式，而这些模式有时候会使我们对某些问题的理解变得狭隘。

特别是在几何学领域，这种现象尤为显著。

比如我们之前谈过的关于欧几里得的第五公设问题，尽管可能偏离了这个公设的核心讨论，但这恰恰帮助我们更深刻地理解几何学中的一些基本问题，因为数学中的定义往往具有主观性和模糊性。

也就是：

“过直线外的一个点，可以做一条，而且仅可以做一条该直线的平行线。至于平行线，就是平面上永不相交的两条线。”

这时就有人犯嘀咕了，会不会经过直线外的一点，能够做出很多条平行线，或者干脆一条也做不出来呢？

19世纪20年代，俄国喀山大学教授罗巴切夫斯基在证明第五公设的过程中，走了另一条路子。

他提出了一个和欧氏平行公理相矛盾的命题，用它来代替第五公设，然后与欧氏几何的前四个公设结合成一个公理系统，展开一系列的推理。

经过细腻的推理，他得出一个违背直觉但是逻辑有没有问题的命题。

最后，罗巴切夫斯基得出两个重要的结论：

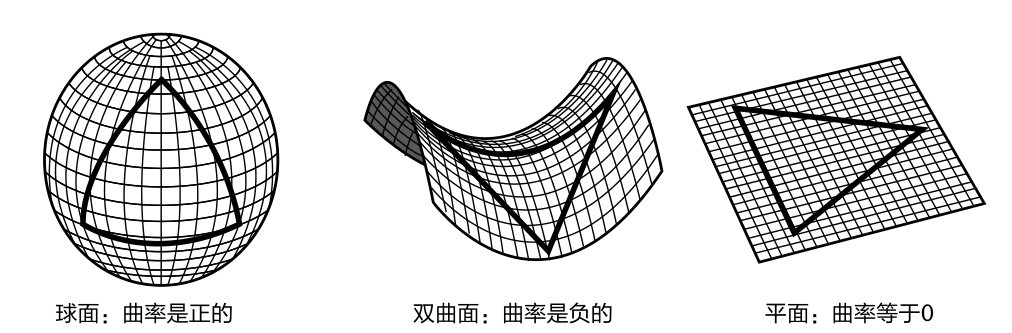
第一，第五公设不能被证明。

第二，在新的公理体系中展开的一连串推理，得到了一系列在逻辑上无矛盾的新的定理，并形成了新的理论。这个理论像欧氏几何一样是完备、严密的几何学。

这种几何学被称为罗巴切夫斯基几何，简称罗氏几何。

这是第一个被正式提出的非欧几何学。当时罗巴切夫斯基把论文寄给俄罗斯的科学院。

科学院主要的科学家一看，过直线外一点可以引两条平行线，认为是离经叛道的歪理邪说。

这几个数学家决定，以后不再审议罗巴切夫斯基有关这方面的论文了。

当然，懂物理学的人都知道，其实这是相对论的起源的基础。

01 误解的根源：孩子的视角

当孩子们初次接触几何形状时，他们的认知往往受到语言的限制，从而导致误解。

例如，图中展示了两个几何形状——一个三角形和一个正方形。

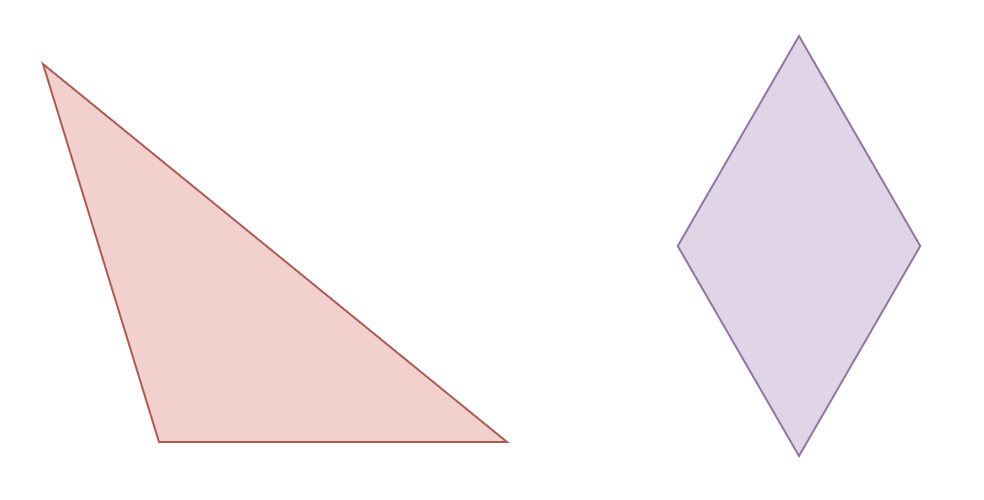
令人意外的是，许多六七岁的小学生会坚持认为，第一个图形不是三角形，而第二个图形也不是正方形。

这种误解源于他们对“标准”形状的接触过少。

在他们的认知中，三角形通常是等边三角形，而正方形则是一个没有旋转过的“正”形状。因此，当他们看到略有不同的形状时，便会不自觉地否定其归类。

这种对于形状的误解并不仅限于儿童。

即便是成年人，也会在某些情况下陷入类似的困惑。

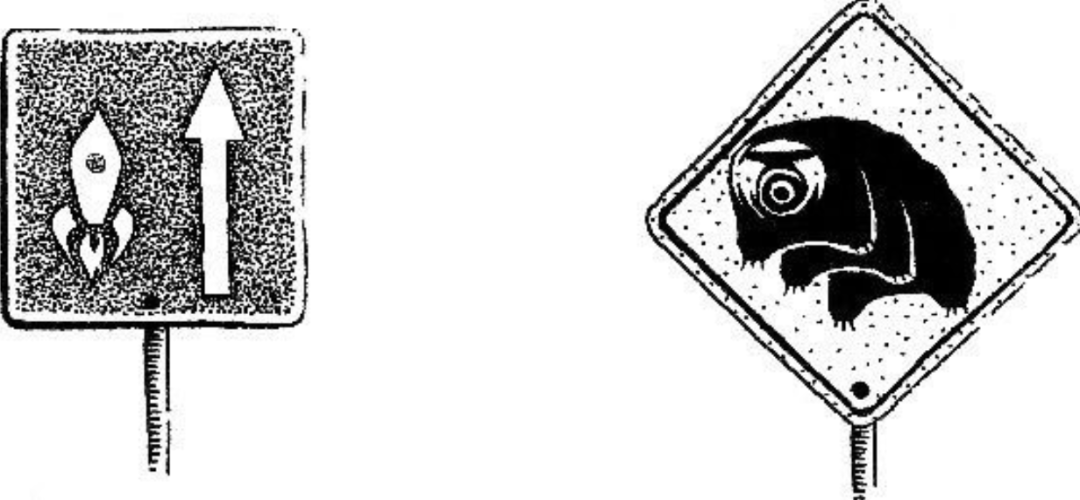
例如，如果我们向一些驾驶员展示两个路标，其中一个是标准的正方形，另一个则是稍微倾斜的正方形，许多人仍然会犹豫是否应该将第二个图形称为正方形。

这种现象揭示了一个事实：我们对于几何形状的定义并非总是绝对的，而是常常受到我们的经验和环境的影响。

02 语言的模糊性：六边形的困惑

为了更深入地探讨这个问题，我们可以进行一个简单的词汇测试。

假设我们将六边形定义为“一个有六条边的图形”，这个定义乍一看似乎非常清晰。

然而，当我们面对实际的图形时，却可能会犹豫不决——什么才算是“边”？

这些边必须是直线吗？

这些边之间是否必须按照某种特定方式排列？

当我们试图通过查阅字典来寻找答案时，结果可能并不如我们预期。事实上，六边形的定义有时可能会更加混乱。

例如，某些字典可能将六边形定义为“一组闭合的六条线段”，按此定义，六边形更像是一个一维的线段集合，而非一个二维图形。

这样一来，上图中的图形实际上都不能算作六边形。

相反，其他更为宽泛的定义则可能允许某些图形被称为六边形，但不包括其他图形。

由此可见，词汇的定义和解释在很大程度上取决于我们如何划定界线。

03 数学家的模糊性：理论与实践的对立

不要以为数学家们会在这些问题上更加理性。他们也常常会根据具体情境采用不同的定义。

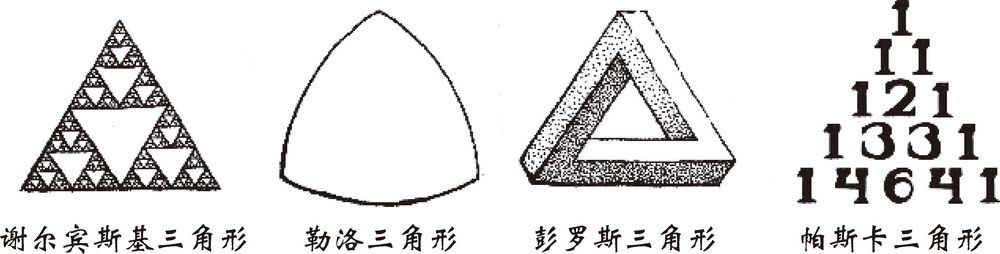
例如，谢尔宾斯基三角形、勒洛三角形、彭罗斯三角形或帕斯卡三角形，从严格的几何意义上来说，这些都不是传统意义上的三角形，但人们仍然愿意称它们为三角形，这样做并无大碍。

我们需要意识到一个重要的事实：语言的模糊性只是表面现象！

这些模糊性是可以被识别和减少的。在日常生活中，我们并不需要在使用词语时达到绝对的精确，只要能够有效沟通即可。

如果在交流过程中出现了歧义，我们只需稍作讨论，便能达成共识。

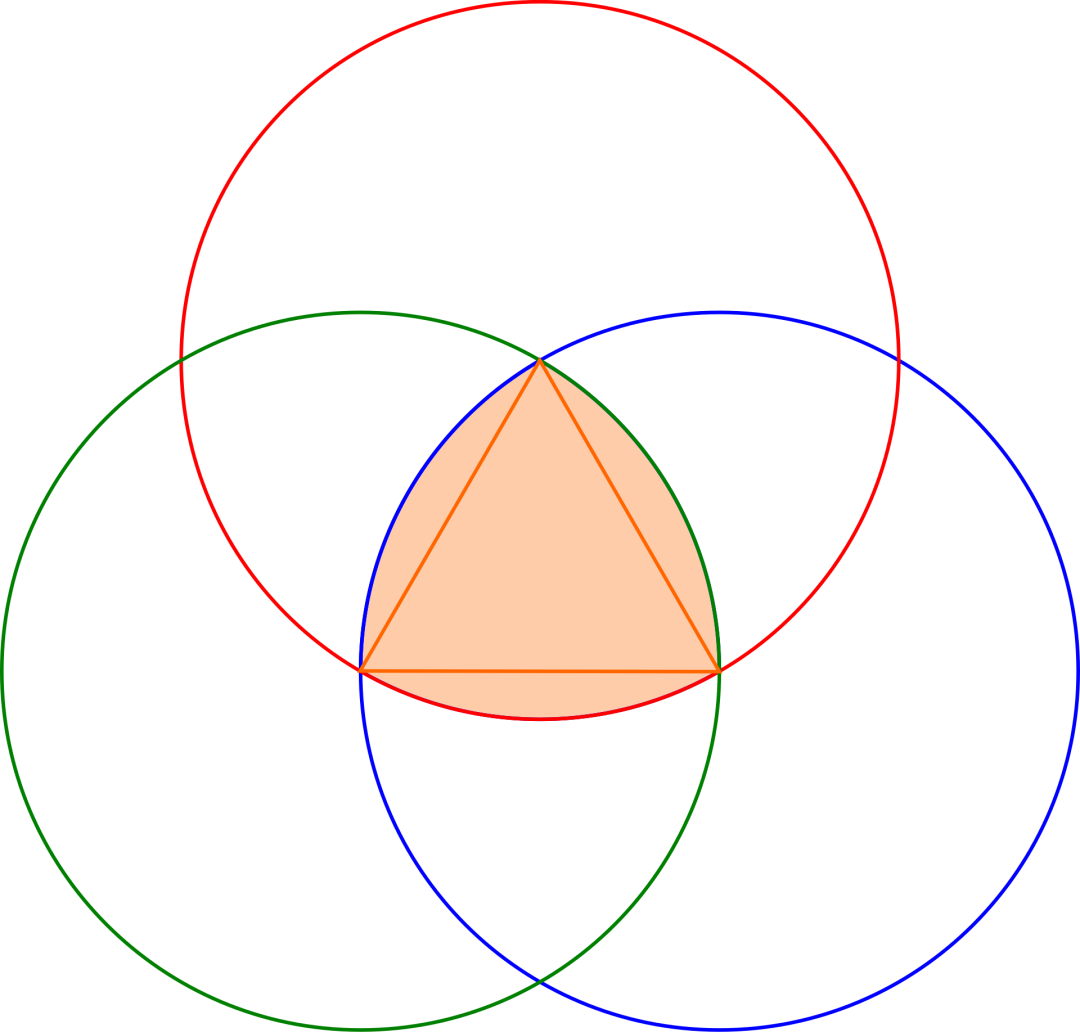
如何绘制一个勒洛三角形

举个例子，当孩子们意识到自己对“三角形”一词的理解有误时，他们会逐渐扩展自己的定义，最终准确地理解这个几何概念。

同样，语言和文化的差异也可以通过学习来克服。

04 感知的差异：我们看同一个世界吗？

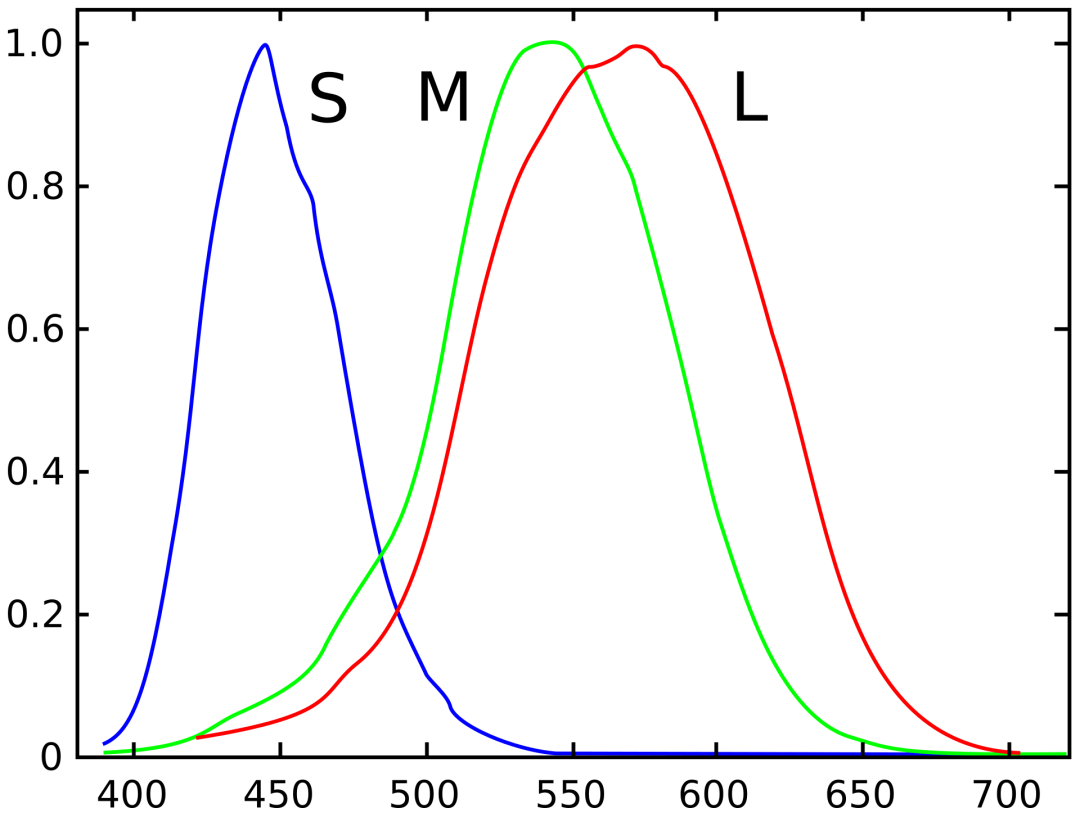
人类（S、M、L 类型的）锥状细胞对单色光谱刺激的规范化典型反应

假设你看到的颜色与他人看到的颜色完全相反。

比如，你看到的蓝色其实是别人眼中的红色，反之亦然。

这不是色盲的情况，而是你感知的颜色完全颠倒了。

在学习语言的过程中，当你被告知西红柿是红色的，天空是蓝色的，你会自然而然地将这些词语与自己的感知对应起来。

因此，你会认为自己看到的颜色与他人是相同的，即使实际情况可能完全相反。

更令人困惑的是，如果每个人的感知都是独特且无法与他人比较的呢？

或许每个人都有自己所称的“蓝色”，但在别人的色谱中找不到相应的颜色。在这种情况下，比较主观体验的意义何在？

无论如何，这个问题似乎没有答案，因为这种主观性的本质使得任何讨论、问题或经验都无法揭示这些差异。如果误解真的存在，我们可能永远无法察觉。

这种绝对的、没有希望的主观性不仅限于颜色。

味道、声音、气味等感官体验或许也是如此。你尝到的咸味可能是别人尝到的甜味，你听到的低沉声音可能是别人耳中的尖锐声音，你闻到的玫瑰香气可能是别人感知的丁香芬芳。

生活或许只是一场巨大而持续的误解，每个人都在谈论不同的事物，但他们却认为彼此达成了共识。

在这种情况下，交流的可能性并不取决于我们是否谈论相同的事物，而是取决于这些事物之间是否存在相同的关系。或许你眼中的蓝色、红色和紫色与我眼中的完全不同，但你仍然会同意红色和蓝色可以混合成紫色。

这种共识使得我们的交流在某种程度上是真实的，而这或许才是唯一重要的事情。

那我么讨论数学的时候，如何辨别真假？

在《几何原本》中，欧几里得使用了诸如“点”、“线”或“圆”等词语。当我们看到这些词时，脑海中可能会勾勒出相应的形象。但其他人是否也会赋予这些词语不同的含义呢？是否有可能在对这些词语有着不同理解的情况下进行几何讨论呢？

答案是肯定的。

数学本质上是模棱两可的，正如颜色一样，它可能被绝对的主观性所束缚。

事实上，许多理论都可以用不同的方式来解释。

19世纪，人们意识到数学可能受到误解的影响，这一发现既令人震惊，又激发了新的思考。一些富有胆识的天才不仅没有因模糊性而退缩，反而将这一弱点转化为优势。

就像加拿大的森林，有时候需要通过一场大火来焕发新生。在科学的世界里，灾难往往激励着人们去探索新的理论，创造出新的知识体系。

如果事物本身具有模糊性，那么我们何不利用数学来处理这种模糊？让我们创立一个关于模糊的精确理论，学习如何精确地研究不精确的事物吧。

虽然听起来似乎不可思议，但欧几里得的第五公设正是通过放松对含义的严格控制才得以解决。

现在我们明白了，科学家们之所以在两千年间未能解开第五公设的谜团，并不是因为他们对欧几里得几何学的理解不够深入，而是因为他们过于自信地认为自己已经完全理解了所谈论的对象。

最终，灾难被转化为伟大的胜利，而关于模糊性的理论则成为数学史上最为辉煌的成就之一。

结语：

通过对数学中主观性和模糊性的探讨，我们可以看到，科学的发展往往伴随着对既定认知的挑战。

正是在这些模棱两可和不可知的领域中，科学家们找到了新的方向，为未来的探索铺平了道路。

也正是多样性，才有了这个多姿多彩的世界。