
话说,这世间总会存在这样一些问题,就是那些自从被人们提出来之后,便成为人类心中挥之不去的疑问。
我们通过观察和分析世界,逐渐了解并相信一些自然的机制,尤其是当我们看到相同的原因不断地产生相同的结果时,我们更容易产生一种掌握真理的错觉。
但我们对自身认知的信心到底能达到什么程度?
又如何避免成为偏见、运气不佳和错误理解的受害者?
人类能否真正做到对某些事物“确信无疑”而没有任何漏洞呢?
回顾人类认知的历史,不乏一些曾被认为是铁一般事实的观点,最终却被推翻或纠正,比如:
我们曾坚信太阳绕着地球转的地心说,也曾以为几何图形只能存在于三维空间中。
即便是我们的大脑,甚至最伟大的学者也难免会犯错。
科学确实教会了我们许多关于世界的知识,但同时,它也应让我们变得更加谦逊和保持怀疑。
01
公元前5世纪,一位名叫希波克拉底的数学家试图通过解决几何学的基本问题来消除这种怀疑。他着手撰写了一部关于几何的书籍,试图系统地总结和阐述几何领域已知的成果。
这部著作的目标是雄心勃勃的:组织并奠定几何学的坚实基础,使其建立在无可辩驳的真理之上。在这部书中,任何论断都不应轻率下结论,所有的定理都应经过严谨的验证。
然而,希波克拉底的著作并未流传至今,随后的几个世纪里,继任者们的著作也未能逃过时间的摧残。
但到了公元前3世纪,随着另一位伟大学者欧几里得的出现,几何学的命运发生了重大转变。

当然是欧几里得完成了一部史上最完整、最具影响力的几何学著作——《几何原本》。
这部著作共十三卷,内容涵盖了平面几何、算术、比例以及三维几何的问题。
欧几里得以系统化和严密的逻辑推理,将几何学知识从最简单的性质到最复杂的定理逐步建立起来。
《几何原本》不仅在数学史上树立了一个里程碑,更为几何学奠定了坚实的理论基础。
在《几何原本》问世后,虽然后世的学者对其内容进行了一些修订和扩充,但欧几里得所奠定的整体结构从未遭到质疑。自此,数学似乎走上了正轨,有了坚固可靠的基石。
《几何原本》让数学家们相信,他们所提出的论断是可以经得起推敲的。
然而,这个故事并没有就此结束。
02
因为《几何原本》的核心部分,尤其是其中的第五公设,孕育出了一个全新的问题,这个问题挑战了之前所有文明的认知,并引发了长达两千年的科学探讨。
第五公设,被认为是科学史上的一座丰碑,甚至可以称为史上最伟大的数学谜题。
这个谜题独特且影响深远,其解决之道不仅仅在于其本身的数学意义,更在于它对数学本质的重新定义。
要理解它,我们必须深入了解《几何原本》的结构及其方法。
《几何原本》之所以卓越,不仅仅因为其数学成果,更因为它所确立的推理方法。书中的每一个定理都必须经过严格的证明,所有论断都基于先前已经证明的结果,从而通过逻辑推理来确保其准确性。
然而,这种方法也面临着一个不可避免的挑战:推理必须从某个已知的基础开始。
那么,最初的知识又该基于什么呢?
《几何原本》作为几何学的奠基之作,如何证明其第一个命题呢?
希波克拉底、欧几里得以及其他希腊学者都明白,这里没有奇迹可言。要让数学这部机器运转起来,必须接受一些未经证明的初始论断,即公理。
欧几里得选择了五个公设来构建平面几何,其中最为复杂的就是第五公设,即关于平行线的公设。
第五公设:过直线外的一个点,可以做一条,而且仅可以做一条该直线的平行线(平行公理)。至于平行线,就是平面上永不相交的两条线。
与其他四个公设相比,第五公设的表述更加复杂,因此它并不如其他四个公设那样“显而易见”。然而,这个公设却成为了几何学中最具争议的部分,甚至在长达两个多世纪的时间里,它困扰着一代又一代的数学家。
数学史上,很多学者都希望能够简化几何学的基础,甚至有人尝试通过减少公设的数量来重构几何学。特别是,有人提出能否只用前四个公设来构建整个平面几何,而无需依赖第五公设。
这个问题看似简单,但实则复杂无比,成为了一个困扰了几代数学家的难题。
虽然在欧几里得撰写《几何原本》时,显然已经考虑到了这个问题,但具体是在何时首次提出我们已无法得知。无论这个问题最初是何时出现,它都引发了远超几何学范畴的科学巨变。
两千年来,数学家们不断努力,希望证明第五公设是否真的是必不可少的。
最终,在19世纪,这个谜题终于得到了答案,但解决它所引发的科学震荡,远远超出了人们的想象。
这一简单的几何问题,最终促成了非欧几何学的诞生,并对整个科学界产生了深远的影响。
第五公设的解决方法并不复杂,但它的优雅在于它需要我们改变看待问题的方式。
两千年来,许多才华横溢的学者将自己的一生奉献给了这个问题,但始终未能成功。然而,当我们从一个全新的角度看待它时,解决办法竟变得如此显而易见。
欧几里得的《几何原本》不仅奠定了几何学的基础,更为数学提供了一种新的思维方式。
这种严密的逻辑推理方法成为了后世数学发展的基石。虽然在数学发展的历程中,不断有新的理论出现,甚至一些经典理论被推翻或修正,但《几何原本》所代表的精神——追求严谨和逻辑——却始终未变。
今天,我们已经不再会对第五公设的问题产生争论。
数学家们普遍认为,建立在尽可能少的定理之上的理论才是最优的。然而,正是这些看似简单的问题,促使数学不断前进,甚至引发了科学的G命。
补充:
在19世纪,几位数学家——主要包括俄罗斯的尼古拉·罗巴切夫斯基、匈牙利的扬诺什·鲍耶和德国的卡尔·弗里德里希·高斯——独立地发展了非欧几何学。
他们放弃了欧几里得的第五公设,探讨了如果假设第五公设的否定会发生什么。
这些数学家们发现,即使不接受欧几里得的第五公设,依然可以构建出一套完全一致且自洽的几何学体系,这些体系后来被称为“非欧几何”。
在罗巴切夫斯基和鲍耶的几何学中,平行线的概念被重新定义,他们假设在给定一条直线和直线上一点时,可以画出多条直线与之平行。
这种几何学后来被称为“双曲几何”。
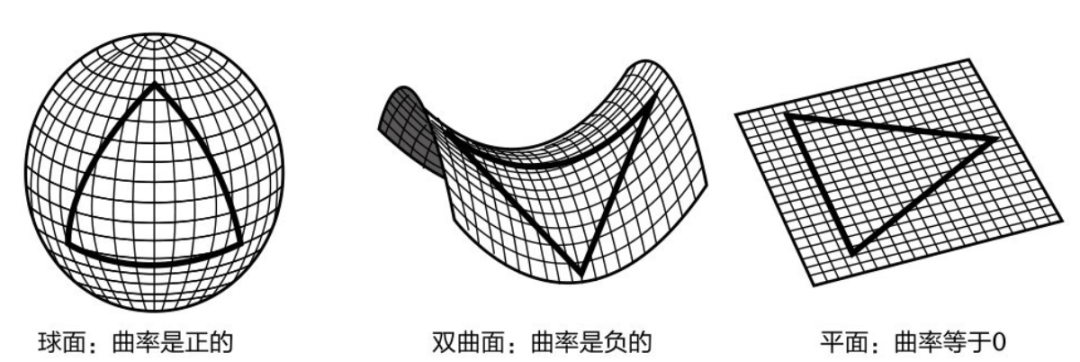
与此同时,德国数学家贝尔纳德·黎曼提出了另一种不同的几何学形式,假设通过一个点不可以画出任何一条直线与已知直线平行,这种几何学被称为“椭圆几何”。
这些非欧几何学的发现表明,第五公设并不是唯一可能的公设,几何学并非必须建立在它的基础上。
换句话说,欧几里得几何学只是可能存在的几何学之一,而不是唯一的几何学。
非欧几何学的出现不仅解决了困扰数学家两千多年的问题,还为20世纪物理学的重大突破——爱因斯坦的广义相对论——提供了理论基础。
广义相对论表明,空间并非绝对平坦,而是可以弯曲的,这与非欧几何的思想高度契合。
因此,第五公设的问题不仅得到了圆满的解答,还打开了数学和科学的全新领域,彻底改变了我们对宇宙结构的理解。
这一结论不仅标志着数学的进步,也昭示着我们对世界的认识将永远处于不断演进和扩展之中。
总结:
回顾历史,我们不禁感叹,那些曾经困扰无数学者的数学谜题,最终不仅推动了科学的发展,还改变了我们对世界的理解。而欧几里得的遗产,也将在未来继续引领我们探寻数学和科学的未知领域。
这一切,既是历史的必然,也是人类智慧的结晶。正如第五公设的谜题一样,数学的魅力在于它的复杂与简单并存,挑战与优雅并存。
这种矛盾与统一,正是科学探索的不竭动力,也是数学世界永恒的美丽。

















