在经典物理学的框架下,带电粒子在做加速运动时会不断向外辐射电磁波,进而损失能量。而原子内的电子绕着原子核做类似行星绕太阳的运动,如果依照经典电磁理论,电子应当逐渐失去能量,最终坠入原子核。但现实中,电子并没有耗尽其能量,而原子保持稳定,这一现象曾经是物理学家们长期探讨的问题,直到量子力学的诞生才真正解开谜团。
1. 经典物理学的困境
在19世纪末,经典物理学家通过电磁学理论研究带电粒子的运动时,提出了电磁波辐射理论。根据麦克斯韦方程组,带电粒子在加速时会产生电磁辐射,进而损失能量。将这一理论应用于原子模型,电子围绕着带正电的原子核旋转,受到库仑力的作用,这一加速运动必然会导致电子逐步向外辐射能量。
根据经典电磁理论,电子会不断损失能量,导致它的轨道半径逐渐减小,最终坠入原子核。这意味着原子应该是不稳定的,电子在短时间内就会坍缩。然而,自然界中我们观察到的事实是,原子是稳定的,电子并没有坠入原子核,这给经典物理学带来了巨大的挑战。
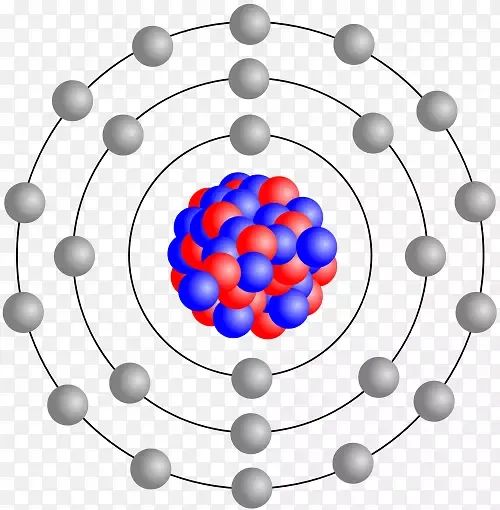
2. 玻尔模型的提出与突破
面对经典物理学解释原子结构的困境,1913年,尼尔斯·玻尔提出了著名的玻尔原子模型。这一模型成功解释了氢原子的稳定性以及原子光谱的离散特征。
玻尔模型的核心思想是:电子只能在某些特定的轨道上绕原子核旋转,这些轨道对应的是固定的能量状态。在这些轨道上,电子不会向外辐射能量,只有当电子从一个高能级跃迁到低能级时,才会辐射出特定频率的光子。玻尔通过引入量子化条件,即角动量只能取某些离散值,成功解释了氢原子的光谱。
玻尔的模型为理解原子的稳定性提供了一个初步的解释,但仍然依赖了一些经验性假设,无法从根本上解决问题。电子为什么只能在某些轨道上运动,且这些轨道为何不会辐射能量,这些问题仍未得到彻底解答。

3. 量子力学的诞生:电子波动性与轨道稳定性
随着20世纪量子力学的逐渐成熟,科学家们对电子在原子中的行为有了更加深入的认识。根据路易·德布罗意的波动假设,电子不仅具有粒子性质,还具有波动性质。电子在原子中的运动不再被简单地看作是一个绕核旋转的粒子,而是作为概率波的分布。
量子力学中,电子的状态由薛定谔方程描述,这一方程为电子提供了可能存在的空间分布。通过解薛定谔方程,我们可以得到电子的波函数,电子的运动轨迹不再是经典的圆形或椭圆形轨道,而是概率云。这些云状区域表示电子在不同位置出现的概率分布。
关键在于,电子的能量状态是量子化的,即电子只能处于特定的能级,无法处于这些能级之间的过渡状态。在这些量子化的轨道上,电子的波动性使其在稳定状态下不会继续辐射能量。这一现象完全违背了经典物理学对粒子加速运动辐射的认知。
4. 能级跃迁与光子辐射
在量子力学中,电子只有在发生能级跃迁时才会辐射或吸收光子。当电子从较高能级跃迁到较低能级时,会释放出特定频率的光子,这种辐射遵循能量守恒定律,光子的能量等于两个能级之间的能量差。反之,电子吸收能量时,也会跃迁到更高的能级。
这就解释了为什么电子不会在稳定的轨道上辐射能量——因为在这些轨道上,电子的状态是稳定的,不会发生能量的自发损失。只有当外界能量作用于原子时,电子才会发生跃迁,从而辐射能量。
5. 不确定性原理与电子的空间约束
量子力学的另一个重要概念是不确定性原理。根据海森堡的不确定性原理,电子的动量和位置无法同时被精确确定。这意味着电子并不是像经典物理学描述的那样在固定轨道上运行,而是具有一定的空间不确定性。这种不确定性使得电子的行为更像是一个围绕原子核的波包,而非一个精确的粒子轨迹。
正是这种量子不确定性保证了电子不会无限接近原子核,也因此避免了坠入原子核的命运。
6. 量子电动力学与电子自发辐射问题
虽然量子力学解决了原子结构的稳定性问题,但科学家们仍在探讨电子在复杂条件下的行为。例如,在量子电动力学(QED)中,电子的自发辐射问题得到了进一步的解释。QED是一种描述电磁相互作用的理论,它能够更加精确地预测带电粒子之间的相互作用,并解释了电子在极端条件下的辐射行为。
QED认为,即便在稳定的轨道上,电子也会与真空中的虚拟光子发生微弱的相互作用,但这种辐射极为微弱,不足以影响电子的整体能量状态,从而维持了原子的长期稳定性。
7. 科学意义与未来展望
对电子能量辐射问题的深入探讨,不仅让我们更加了解了原子的稳定性问题,还推动了量子物理的进一步发展。通过研究电子在原子中的行为,我们揭示了量子力学的许多核心概念,如能级量子化、波粒二象性与不确定性原理。这些理论不仅为理解微观世界奠定了基础,也为未来的技术应用提供了广阔的前景。
展望未来,随着实验技术的进步,我们将能够更加精确地观察和操控电子的运动,这将为我们进一步揭示物质结构的奥秘提供更多机会。
总结
从经典物理学的困惑,到量子力学的突破,再到现代量子电动力学的精细描述,电子在原子中的行为揭示了微观世界的奇妙复杂性。通过量子力学的框架,我们不仅解释了电子为何不会因辐射能量而坠入原子核,还揭示了自然界深层次的规律。这一研究不仅解开了原子结构的稳定性之谜,也为我们提供了探索物质基本性质的新思路。

















