在人工智能和语言学的交叉领域,一项突破性研究在国际上引起广泛关注。2024年度计算语言学协会(ACL)最佳论文奖授予了题为《不可能任务:语言模型》的研究,该论文不仅展示了精巧的实验设计,更大胆挑战了语言学泰斗乔姆斯基的观点。

图片来自网络
长期以来,乔姆斯基等语言学家坚持认为,大型语言模型(LLM)同样能够学习人类可能和不可能的语言。这一观点若成立,将极大削弱LLM在语言研究中的价值。然而,斯坦福大学的Julie Kallini等研究者通过一系列巧妙的实验,首次系统地检验并否定了这一假设。他们的研究表明,LLM确实难以学习"不可能语言",这一发现为LLM在语言学研究中的应用开辟了新的可能性。

对于正在开发AI产品的Prompt工程师而言,理解LLM的语言学习机制至关重要。
01
乔姆斯基的观点与争议
诺姆·乔姆斯基是现代语言学的奠基人之一,他的理论对语言学研究产生了深远影响。近年来,随着大型语言模型的兴起,乔姆斯基对这些模型的语言学习能力提出了质疑。他认为,LLM"无法区分可能和不可能的语言",这种特性"不可能被修改"。

图片来自网络
乔姆斯基的观点得到了一些语言学家的支持。例如,Moro等人声称,"LLM可以产生'不可能'的语言输出,其效果不亚于(如果不是更好于)自然语言输出"。这些强烈的断言似乎否定了LLM在语言研究中的价值。以下这篇文章中有关于乔姆斯基语义分析的观点(由claude2生成)
然而,这些观点很大程度上缺乏实验证据的支持。在Kallini等人的研究之前,唯一被广泛引用的相关实验研究是Mitchell和Bowers在2020年的工作。尽管该研究很重要,但仅凭一项研究难以得出如此宏大的结论。
02
不可能语言:一个模糊的概念
研究的一大挑战在于,"不可能语言"本身是一个难以明确定义的概念。语言学家们对什么构成了人类语言的普遍特征,以及哪些特征是"不可能"的,尚未达成共识。
为了克服这一困难,Kallini等人提出了一个"不可能性连续体"的概念。在这个连续体的一端是直观上显然不可能的语言,如随机打乱的英语单词序列。另一端则是那些可能不那么直观,但在语言学中常被认为是不可能的语言,如基于数词位置的语法规则。
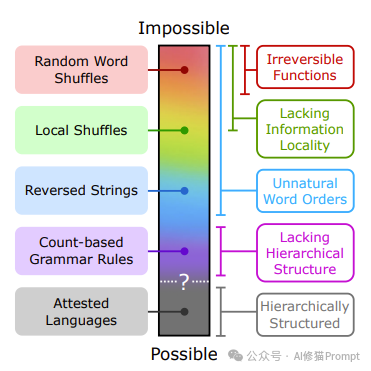
这张图展示了语言的"可能性连续体",从不可能的语言结构到可能的语言结构。图中从上到下依次呈现了不同类型的语言特征,并用颜色编码标示了它们在这个连续体上的大致位置。
1. 最上方(粉色)是"随机单词打乱"(Random Word Shuffles),被归类为最不可能的语言结构。
2. 接下来(浅绿色)是"局部打乱"(Local Shuffles),略微靠近可能的一端。
3. 然后是"反转字符串"(Reversed Strings),用蓝色表示。
4. 再往下(紫色)是"基于计数的语法规则"(Count-based Grammar Rules)。
5. 最下方(灰色)是"已证实的语言"(Attested Languages),代表自然存在的人类语言,位于可能性的一端。
图的右侧列出了一些相关的语言特征:
- 不可逆函数
- 缺乏信息局部性
- 不自然的词序
- 缺乏层次结构
- 具有层次结构(与已证实的语言相关)
中间的虚线和问号表示可能和不可能语言之间的模糊边界。这张图有效地总结了研究中探讨的不同类型的语言结构,并直观地展示了它们在可能性谱系上的相对位置。
研究者们精心设计了一系列合成的"不可能语言",每种语言都通过系统地改变英语数据的词序和语法规则而创建。这些语言涵盖了不可能性连续体的不同位置,为实验提供了丰富的测试材料。
03
实验设计:挑战LLM的极限
研究团队设计了三组主要实验,旨在全面评估GPT-2小型模型学习这些不可能语言的能力。实验的核心是研究者合成了一组不可能的语言。通过定义英语句子的扰动函数来指定不可能的语言。这些扰动函数将英语输入句子映射到标记序列。研究者将语言分为三类:*SHUFFLE、*REVERSE和*HOP每类下包含几种不同的语言变体。每种语言都给出了两个例句,以展示其特定的规则和结构。
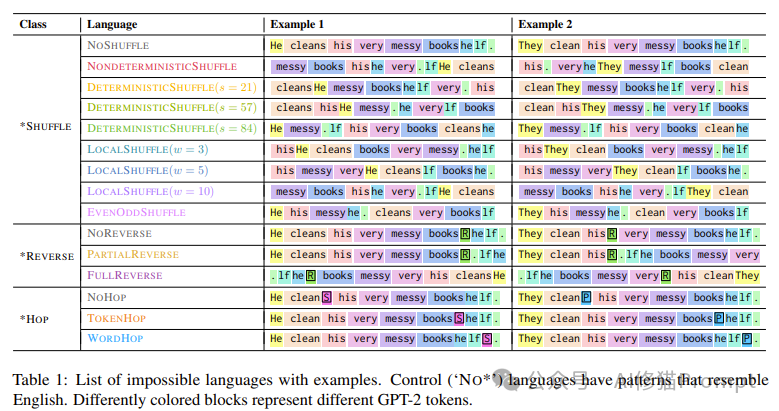
1. *SHUFFLE类:
- NOSHUFFLE:保持原始英语句子结构,作为对照组。
- NONDETERMINISTICSHUFFLE:完全随机打乱单词顺序。
- DETERMINISTICSHUFFLE:基于特定规则(如种子值)确定性地打乱单词顺序。
- LOCALSHUFFLE:在固定大小的窗口内局部打乱单词顺序。
- EVENODDSHUFFLE:将句子中的偶数位置词和奇数位置词分开重排。
2. *REVERSE类:
- NOREVERSE:在句子中随机插入一个特殊标记R,但不改变词序,作为对照组。
- PARTIALREVERSE:插入R标记,并反转其后的所有单词。
- FULLREVERSE:插入R标记,并完全反转整个句子。
3. *HOP类:
- NOHOP:将动词原形后直接加上表示单复数的标记(S或P),作为对照组。
- TOKENHOP:将单复数标记放在动词后的第4个词元位置。
- WORDHOP:将单复数标记放在动词后的第4个单词位置。
这些例子清晰地展示了每种"不可能语言"的具体规则和结构。
实验一:学习效率比较
在第一个实验中,研究者们训练GPT-2模型学习一系列预先定义的可能和不可能语言,并通过测试集困惑度(perplexity)来衡量学习效率。困惑度是评估语言模型性能的常用指标,较低的困惑度表示模型对语言的预测更准确。
研究者的假设是,训练在可能语言上的模型会更快达到较低的平均困惑度(以训练步骤衡量)。这个实验直接比较了LLM学习不同类型语言的能力。
实验二:语法规则敏感性测试
第二个实验更深入地探讨了一组特殊的不可能语言:基于计数的动词标记规则。研究者使用惊奇度(surprisal)比较来针对性地检验相关模式。
惊奇度衡量了模型对某个词的预期程度,它是该词在给定上下文中出现概率的负对数。较高的惊奇度意味着模型对该词的出现更感意外。
研究者假设,对于可能语言,模型在面对不合语法的结构时会表现出更高的惊奇度。这个实验旨在检验GPT-2是否能够习得并遵循这些基于计数的语法规则。
实验三:因果抽象分析
在第三个实验中,研究者更深入地探究了模型内部机制,试图理解GPT-2如何发展出学习这些基于计数的语法规则的能力。他们采用了因果抽象分析方法,这是一种解释神经网络内部工作原理的技术。
这个实验的目标是揭示模型是否为这些不自然的语法模式发展出某种自然、模块化的解决方案。
04
实验结果:挑战乔姆斯基的断言
三组实验的结果都强有力地挑战了乔姆斯基等人的观点,表明GPT-2确实难以学习不可能语言。
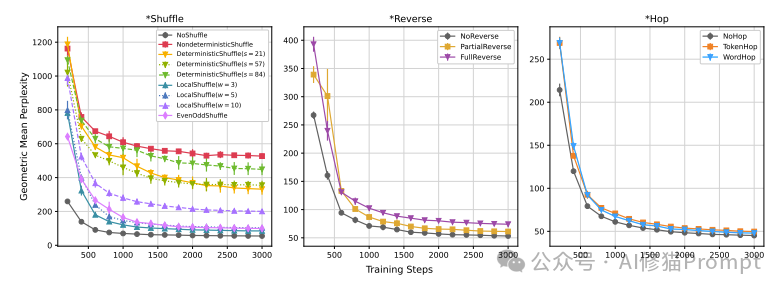
这组图表展示了三类"不可能语言"(*Shuffle、*Reverse和*Hop)在训练过程中的学习曲线。横轴表示训练步骤,纵轴表示几何平均困惑度(Geometric Mean Perplexity)。困惑度是衡量语言模型性能的指标,数值越低表示模型表现越好。
1. *Shuffle图:
- NOSHUFFLE(未打乱的英语)的困惑度最低,学习最快。
- NONDETERMINISTICSHUFFLE(完全随机打乱)的困惑度最高,学习最慢。
- DETERMINISTICSHUFFLE和LOCALSHUFFLE的表现介于两者之间,且保留更多局部结构的变体(如较小窗口的LOCALSHUFFLE)表现更好。
- EVENODDSHUFFLE的表现接近NOSHUFFLE,说明它保留了一定的语言结构。
2. *Reverse图:
- NOREVERSE(未反转的英语)表现最好。
- PARTIALREVERSE和FULLREVERSE的表现相近,但略差于NOREVERSE。
- 三种模型的学习曲线差异不如*Shuffle组明显。
3. *Hop图:
- 三种模型(NOHOP、TOKENHOP、WORDHOP)的表现非常接近。
- NOHOP(最接近自然英语的版本)略微领先。
- 学习曲线快速收敛,说明模型相对容易学习这类规则。
这些结果强有力地支持了研究的核心发现:
1. GPT-2确实在学习"不可能语言"时表现出困难,特别是那些完全打乱或反转词序的语言。
2. 保留更多自然语言结构的变体(如NOSHUFFLE、NOREVERSE、NOHOP)始终表现最佳。
3. 局部结构的保留(如LOCALSHUFFLE)有助于模型学习。
4. 基于计数的语法规则(*Hop类)相对容易学习,可能是因为它们保留了大部分原始句子结构。
这些图表有力地反驳了乔姆斯基等人的断言,证明大语言模型确实能够区分可能和不可能的语言结构,并在学习过程中表现出对自然语言结构的偏好。
学习效率的显著差异
在第一个实验中,研究者发现训练在可能语言上的模型确实能更快地达到较低的困惑度。具体来说:
1. 对于*SHUFFLE语言组(包括各种单词打乱方式),NONDETERMINISTICSHUFFLE(完全随机打乱)模型的困惑度最高,其次是三个DETERMINISTICSHUFFLE模型。这表明GPT-2在学习确定性的打乱模式时表现更好。
2. 局部打乱(LOCALSHUFFLE)模型的困惑度次之,窗口大小越小,困惑度越低。这说明保留一定程度的局部结构有助于模型学习。
3. EVENODDSHUFFLE(奇偶位置分离)和NOSHUFFLE(未打乱的英语)模型困惑度最低,但NOSHUFFLE始终保持领先。
4. 在*REVERSE语言组中,实验模型与控制组(NOREVERSE)的困惑度差距较小,但PARTIALREVERSE略优于FULLREVERSE。
5. *HOP语言组(涉及基于计数的动词标记规则)的模型间差异最小,但控制组仍然表现最佳。
这些结果清楚地表明,GPT-2在学习更接近自然语言结构的语言时表现更好,而对于那些违反自然语言规律的"不可能语言",学习效果明显较差。
语法规则学习的局限性
第二个实验进一步证实了GPT-2难以掌握不自然的语法规则。研究者发现:
1. NOHOP模型(最接近英语的版本)在整个训练过程中始终表现出最低的标记惊奇度和最高的惊奇度差异。这意味着该模型最能准确预测标记的出现,并对标记的缺失最为敏感。
2. TOKENHOP和WORDHOP模型虽然也学会了在正确位置期待标记,但效果不如控制组。TOKENHOP的表现略优于WORDHOP,表明基于词元而非单词的计数规则相对更容易学习。
这些发现表明,虽然GPT-2能在一定程度上学习基于计数的语法规则,但它明显更偏好符合自然语言模式的规则。
模型内部机制的揭示
第三个实验的因果抽象分析提供了模型如何处理这些不自然语法模式的深入洞察:
1. 所有三种*HOP模型都发展出了类似的模块化解决方案来处理主谓一致任务。它们在前几层跟踪主语信息,然后在后几层将这信息转移到需要预测标记的位置。
2. NOHOP模型(最自然的版本)最快形成这种机制,在大约1500训练步骤后就达到了近乎完美的性能。
3. TOKENHOP和WORDHOP模型虽然也形成了类似的机制,但效率较低,需要更多训练才能达到相似的性能水平。
这些结果表明,即使面对不自然的语法规则,GPT-2也试图以一种结构化、模块化的方式来解决问题。然而,它在处理更接近自然语言的结构时明显更有效率。
05
LLM的语言学价值重估
看到这里您或许和我一样,也有这样的疑问和反思,我替您提一个尖锐的问题:凭什么用一个过时的小模型GPT-2就断言结论推翻乔姆斯基观点?如果在Claude 3.5 Sonnet或GPT-4上进行类似实验,结论还会是这样吗?我对ACL研究的学术严谨性产生质疑。
很显然,这些更大、更先进的模型可能展现出更强的学习能力,甚至对"不可能语言"也能表现得更好(研究者提供了代码https://github.com/jkallini/mission-impossible-language-models,但我并未更换高级模型进行测试,如果您有兴趣可以运行一下代码,请告诉我结果,我很有兴趣了解)。高级模型可能在处理长距离依赖和复杂语法规则方面有明显优势。甚至,基本趋势(即偏好自然语言结构)可能仍然存在,只是差异可能不那么明显。以上仅是我对反思的假设。
实际上,这项研究获奖,在方法论方面的确提出了创新。尽管模型选择存在局限,但研究的方法论——设计"不可能语言"和进行系统性实验——本身具有创新性和价值。这种方法为评估语言模型的能力提供了新的视角。另外,该研究仍然对语言学理论和人工智能研究提出了有趣的问题,挑战了一些长期存在的假设。理论上的这个贡献可能是获奖的另外一个考量。
我认同的是,这项研究的结果对语言模型研究和开发有着深远的启示:
1. LLM确实能够区分可能和不可能的语言
与乔姆斯基等人的断言相反,研究结果表明LLM在学习人类可能和不可能的语言时表现出明显差异。这意味着LLM可能确实捕捉到了某些与人类语言能力相关的本质特征。了解LLM更容易学习哪些类型的语言结构,可以帮助设计更有效的提示(Prompt)。例如,保持局部结构的完整性可能有助于模型更好地理解和生成内容。
2. LLM作为语言研究工具的潜力
既然LLM能够区分可能和不可能的语言,它们就可能成为研究人类语言普遍性和特殊性的有力工具。研究表明LLM在处理不自然的语言结构时效率较低。因此,在设计提示(Prompt)时应尽量避免使用违反自然语言规律的复杂结构。但似乎最近的火爆的Super prompt又推翻了这一点,但这并不影响你在写Prompt时应该遵循自然语言规律。
3. 模型架构和内部机制的重要性
研究发现,词元化(tokenization)和位置编码等特定的架构决策会影响模型对自然语言的偏好程度。这提示我们,在设计LLM的Prompt时需要谨慎考虑这些因素。例如,利用模型对主谓一致的处理机制来增强生成的连贯性。
4. 自然语言的特殊地位
实验结果反复强调了自然语言结构对LLM学习的重要性。这可能意味着自然语言中确实存在某些本质的、有利于学习的特性。
5. 对"不可能语言"概念的重新思考
研究提出的"不可能性连续体"概念为理解语言的可能性和不可能性提供了新的视角。这可能促使语言学家们重新思考如何定义和研究语言的边界。
6. 充分利用上下文关注模型的局限性
研究显示模型善于利用局部上下文信息。Prompt工程师可以通过提供丰富、相关的上下文来优化模型性能。理解模型在学习某些语言结构时的困难,有助于预测和避免可能的错误。例如,涉及复杂计数或长距离依赖的任务可能需要特别注意。
往期推荐
你以为的LLM上下文学习超能力,究竟来自哪里,ICL的内部机制如何 |最新发布
Kallini等人的研究不仅挑战了乔姆斯基等语言学权威的观点,这项研究也提醒我们,模型和人类在语言处理方面仍存在根本差异。例如,模型对词元的依赖,以及人类对形态边界的敏感性,都是需要进一步研究的重要差异。
同时这项研究也提醒我们,在追求工程应用的同时,不应忽视对模型基本能力和局限性的科学探索。只有将工程实践与科学研究紧密结合,我们才能开发出更强大、更智能的应用。

















