怀尔斯证明费马大定理有三大要素：椭圆曲线、模形式、谷山-志村猜想，此篇介绍其二。

拉马努金是数学神才，他发现了数不尽的奇妙的数学公式，他研究这些公式的奇特性质。今天我们就从他写下的一个表达式开始……

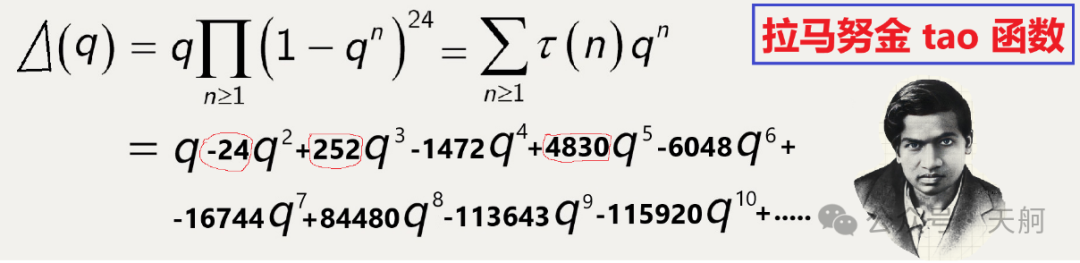
图1：拉马努金tao函数

拉马努金（Ramanujan，1887-1920）研究的，乍一看好像也不是什么深奥的函数，展开后只是一个q的多项式级数而已。不过，拉马努金就是拉马努金，他善于发现一般人看不见的数学奥秘。他考察这个多项式的系数t（n），发现一些特点，比如下面这个，系数t（n）之间有种奇怪的关联：

如果m和n互质，则t（mn）= t（m）t（n）。            （公式1）

比如说，2和3是互质的，t（2）=-24，t（3）=252，计算t（2）xt（3）=-24*252=-6048，正好等于t（2x3）= t（6）。还可以检查别的互质数对应的系数，发现它们都符合（公式1）。

有关这个D（q）函数，拉马努金还发现了其它几个有趣的性质，他把它们总结成了几个猜想，我们不在这儿一一列举了。这种类似的函数还有很多别的，比如：

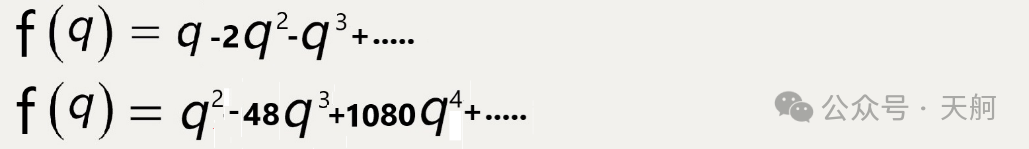
等等。

以上所说的，与 D（q）具有“类似”性质的函数，被数学家们称之为“模形式”，在数学上，模形式（Modular form）被定义为一个上半复数平面上的全纯函数f（z）:

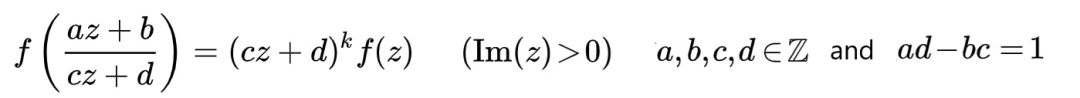
其中k是整数，叫做模形式的权。例如，拉马努金研究的D（z）函数，是权k=12的判别模形式。

比拉马努金更早，模形式还有另外一位老祖宗：德国犹太人数学家爱森斯坦（Einsenstein，1823-1852）。爱森斯坦是喜欢数论的小神童，不幸从小健康不佳，患有脑膜炎等疾病，他于29岁时就死于肺结核。爱森斯坦由于研究数论的原因而研究模形式，并作出重要贡献。爱森斯坦以最简单的模形式“爱森斯坦级数”闻名，另一位同时代的德国数学家克罗内克（Leopold Kronecker ，1823–1891）也对此作出贡献，见图2。

几个世纪以来数学家们一直对模形式丰富的对称性着迷。模形式越来越多地出现在各种各样的问题中：它们是怀尔斯 1994 年证明费马大定理的关键要素；乌克兰数学家，2022年菲尔兹奖得主马林娜用它解决高维空间的球体堆积问题；它们在朗兰兹纲领（“数学大统一理论”）中发挥着核心作用；它们甚至被用来研究物理中的弦论和量子物理学中的模型。

图2：爱森斯坦模形式

在数学的发展过程中，开始时各个领域犹如一个个孤岛，之后，数学家们在孤岛之间架起桥梁，不仅应用不同的知识解决了难题，也建立起新的数学分支。例如，在数论的发展过程中就架起了多个桥梁，发展出了初等数论、解析数论、代数数论和几何数论四个部分。属于解析数论的模形式，便是复分析与数论之间的一座“桥梁”。人们可以通过模形式，利用复分析的工具，来研究整数的性质，解决数论难题。黎曼猜想中使用的黎曼zeta函数也是解析数论中的一个核心函数，它编码了有关素数分布的重要信息。   

为什么模形式更重要呢？因为它是一种在复上半平面上表现出特殊对称性的全纯函数。具有高度对称性的函数在科学研究中有重要的意义，最典型的例子就是三角函数（正弦、余弦函数），它们在物理及工程中的作用广为人知。模形式的对称性是如此惊人和复杂，使模形式比三角函数更为强大，特别是对数论问题而言，它们可用于编码有关整数的深层算术信息。

从模形式f（z）的定义来看，它们在离散矩阵群SL2（Z）的作用下以特定的线性分式的方式变换。模形式的对称性由2×2 的特殊线性群定义，其中矩阵中的四个数字始终为整数。

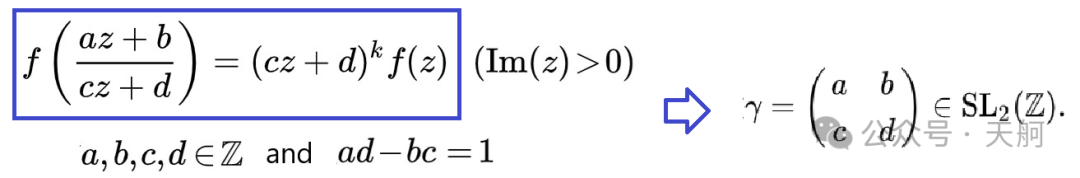
你可能会说，从三角函数的图像就可以看出它们的对称性，而模形式长什么样呢？怎么看出它们的对称性呢？的确如此，复数函数很难形象化，因为它是从一个复数平面映射到另一个复数平面，需要4维图像才能画出来。因此，目前的办法是求助于颜色和亮度，一定程度上也可以看出函数的对称性。

模形式定义在复数的上半平面H，H可以由共形映射转换到单位圆盘D中的点。因此，模形式的对称性可以用一个彩色的单位圆盘D来表示。有时也用H的方形彩色图表示。

例如，下图是判别模形式的图案：

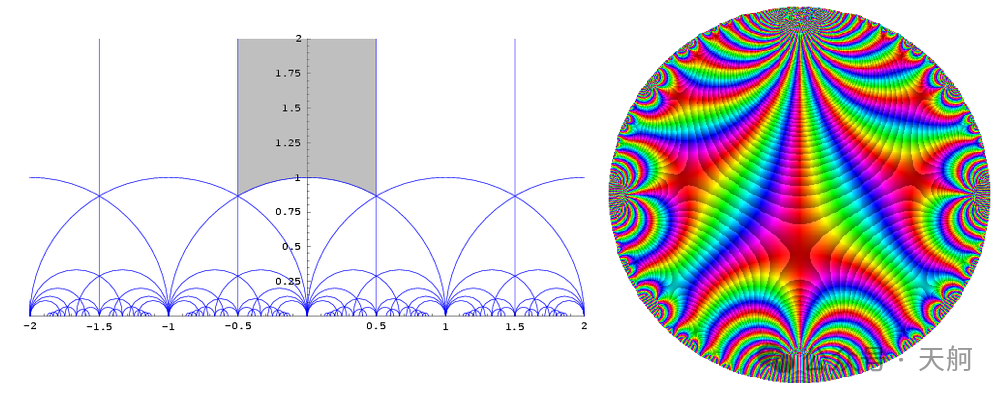
图3：判别模形式

从中可看出，有平移对称性、反射对称性、周期性、和自相似性。

最简单的模形式“爱森斯坦级数”的图像：   

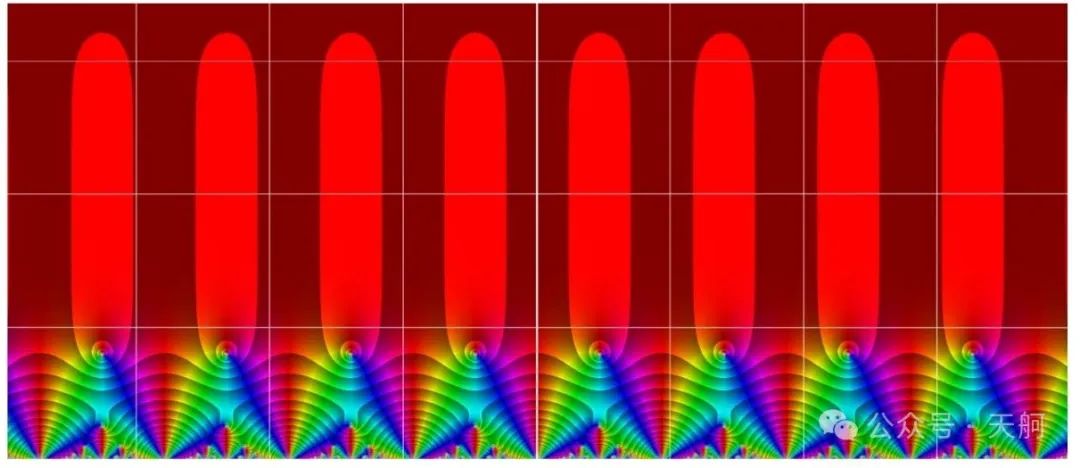
图4：爱森斯坦级数

模形式与椭圆函数密切相关，关键关系在于“模性定理”（之前也称为谷山-志村猜想），我们将于下一篇介绍。

参考资料：

Zagier, D.（2008）. "Elliptic Modular Forms and Their Applications," in The 1-2-3 of Modular Forms（edited by K. Ranestad）, Springer, Berlin, Heidelberg.