你更能接受图 0-1 中的哪种数学教学方式？左边是传统的方式，涉及定义、命题和证明。这种方式的阅读量很大，还包含很多奇怪的符号。你可能很难想到这和几何图形有关。实际上，这段文本解释了如何找到三角形的重心（或形心）。这样的传统教学方法并不会提起我们寻找三角形重心的兴趣。

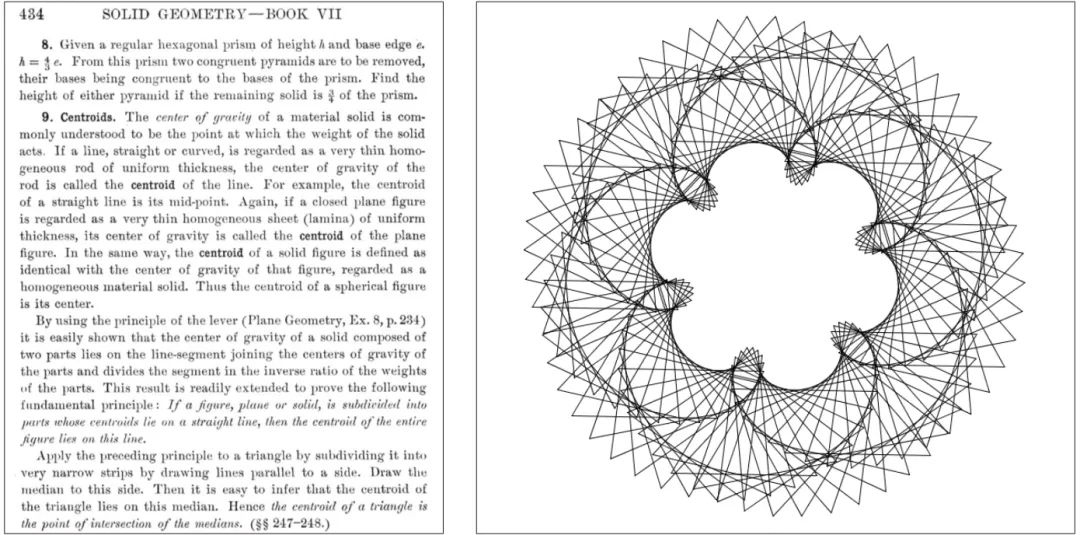
图 0-1　两种教授重心的方式

右边则是一张由约 100 个旋转的三角形组成的动态草图。这是个有挑战性的编程项目，如果你想让三角形旋转得当（而且转得好看），就必须找到它的重心。在很多情况下，不了解几何图形背后的数学原理就画不出精美的图形。你将在本书中看到，我们只需要一点三角形背后的数学知识（比如重心）就能很容易地创造出艺术品。懂数学且会设计的学生更有可能去钻研几何学，不会看到几个平方根或一两个三角函数就被吓跑。然而，只做教科书上的习题却看不到任何结果的学生，恐怕不会有学习几何学的动力。

我做了 8 年数学老师和 3 年计算机科学老师，根据我的经验，喜欢视觉教学法的学生远远多于喜欢学术教学法的学生。在创造有意思的东西的过程中，你会发现数学绝不仅是遵循步骤去解方程。运用编程探索数学能让你发现很多解决有趣问题的方法。你虽然可能会遇到许多始料未及的错误，但这也是提升自己的机会。

这就是学校数学和真实数学之间的区别。

“学校数学”的问题
究竟什么是“学校数学”？在 19 世纪 60 年代的美国，学校数学是为成为记账员所做的准备，就是手动将一列列数字加起来。现在的工作与以往不同，这些岗位的准备工作也要随之而变。

实践是学习的最好方式。但学校并不经常让学生实践，而是更多地让学生被动学习。英语课和历史课上的实践可能是写论文和做演讲，科学课上的实践就是做实验，那数学课呢？以前，数学课上的实践就是解解方程、分解分解因式、画画函数图像。但是现在，计算机可以为我们完成大部分的计算工作，这些实践已经不够了。

学习如何自动化解方程、分解因式和画函数图像并非我们的终极目的。学习自动化某个流程的目的是让学生比以前更深入地研究这个主题。

图 0-2 展示了教科书中的典型数学问题，它要求学生定义函数 f（x），并就大量的 x 对它求值。

图 0-2　教授函数的传统方式

后面还有 18 个同样形式的问题！这种习题对 Python 这样的编程语言来说是小菜一碟。我们只要定义函数发f（x），然后反复从 x 值的列表中取出一个值代入即可：

import math

def f（x）:
    return math.sqrt（x + 3）- x + 1

# 要带入的值的列表

for x in [0,1,math.sqrt（2）,math.sqrt（2）-1]:
    print（"f（{:.3f}）= {:.3f}".format（x,f（x）））
最后一行是为了让输出更好看，将答案保留至三位小数：

f（0.000）= 2.732
f（1.000）= 2.000
f（1.414）= 1.687
f（0.414）= 2.434
在 Python、JavaScript 和 Java 等语言中，函数是转换数和其他对象（甚至其他函数）的重要工具！你可以给 Python 里的函数命名，让人更容易明白它是做什么的。举个例子，可以将一个计算矩形面积的函数命名为 calculateArea（）：

def calculateArea（width,height）:
伯努瓦 • 芒德布罗（Benoit Mandelbrot）在为 IBM 工作期间首次在计算机上生成了他的著名分形。数十年后，一本于 21 世纪出版的数学教科书展示了一张芒德布罗集的图像，并对这一发现大加赞扬。那本书将图 0-3 所示的芒德布罗集描述为“一个从复数中衍生出的迷人的数学对象，它的边界混乱而又美丽”。

图 0-3　芒德布罗集

接着，那本教科书带领读者进行了一次痛苦的“探索”，教学生如何变换复数平面内的一个点。糟糕的是，它只教了如何用计算器变换。这意味着在相当长的时间内只能变换两个点（每个点的变换一般包含 7 次迭代计算）。对，只有两个点。

在本书中，你将学到如何用 Python 程序自动变换几十万个点，甚至画出上面的芒德布罗集图像！

1.用Python体验“全新”的数学不为解题，不记公式，彻底摆脱枯燥——纯粹好玩，自由发挥想象，自己动手制作趣味数学

2.用Python让数学活起来看得见动起来充满立体感的“活”数学，像魔法一样解决常见数学问题

3.涵盖中学数学重要主题，如代数学、几何学、三角学和微积分

4.各种让人欲罢不能的案例，编程与数学强强联合本书以趣味探险路线展示案例，让你真正领略数学的实用性与编程的趣味性

5.Python 3案例，充分展示Python特色与Python可视化的强大

数学拥有无穷的力量。它既帮助游戏开发工程师建模物理世界，也帮助量化金融分析师赚取利润，还帮助音频处理工程师制作音乐。在数据科学和机器学习领域，数学知识更是不可或缺的。

代码和数学是相知相惜的好伙伴，它们基于共同的理性思维，数学公式的推导可以自然地在编写代码的过程中展开。

500余幅图片，本书以图文结合的方式帮助你用Python代码解决程序设计中的数学问题。300余个练习，通过边学边练，你会发现线性代数和微积分的重要概念跃然纸上、印在脑中。