Common Core是美国教育研究领域的亲生子。上一篇(中美教学体系大碰撞 | 低龄数学教育,我们能做些什么?)列出了美国数学教育研究中的一些研究成果,那些都是相对于独立单一数学概念和教学方法的研究。
另外还有一系列的研究涉及参与的教授数量更多,时间更长,结果更震惊。那就是跨国数学教育的对比研究。其中最大型的一个研究叫TIMSS(Trends in International Math and Science Study)
(具体信息和数据在这俩网站 https://nces.ed.gov/timss/ 和 http://timssandpirls.bc.edu/index.html)
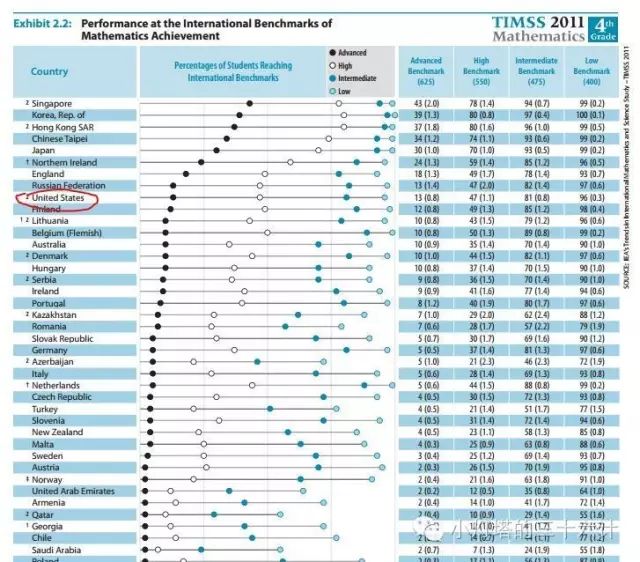
从1995年开始,每隔四年,对包括美国在内的几十个国家地区的四年级和八年级学生进行数学能力考核。如果说奥数是尖子生的竞赛,TIMSS体现的就是大众学生的真实水平。不比不知道,一比吓一跳。美国虽然算不上倒数,但是最多只在第十名左右晃悠。而且虽说是第十名左右,但是跟前五名(新加坡,韩国,日本,香港,台北(中国没参加))完全不是一个重量级别的。
比如四年级的总体情况
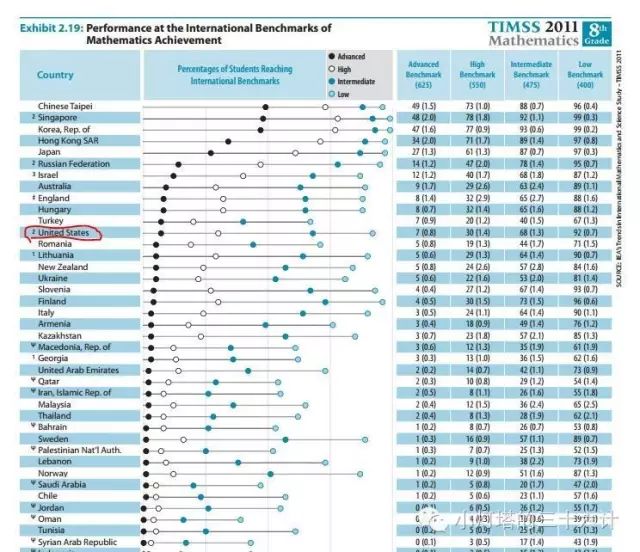
八年级的总体情况
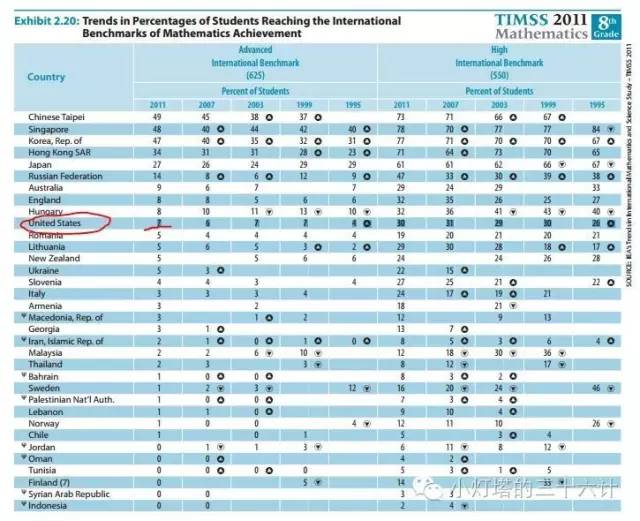
八年级的对数学达到深刻理解程度的学生比例
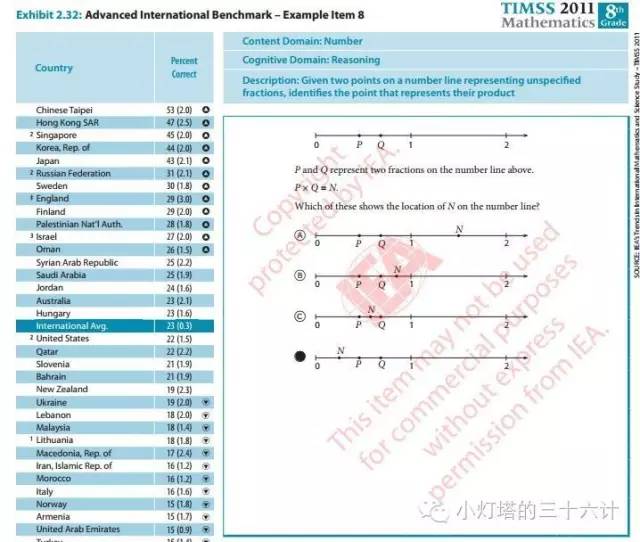
而且看例子,这八年级的深度理解的要求也绝不是什么奥数级别的,比如这个,其实就是两个0-1之间的小数相乘,值在什么范围内。
图片内容来源:
http://timssandpirls.bc.edu/timss2011/downloads/T11_IR_M_Chapter2.pdf
不仅跟前五名的亚洲国家地区的水平差别大,更麻烦的是八年级的比四年级的差别更大。就是说,美国学生在学校里学的年数越多,水平落后越大,学校教学的责任完全无法逃脱。这些数据就是为什么连总统都在担心美国学生的数学水平落后,都在鼓励改进教学。
于是,很多数学研究的机构和教授都潜心研究美国的数学教学和这几个亚洲地区教学的区别。这些对比研究中,找到的最大的区别之一就是教学大纲和教科书。
Common Core之前美国是没有统一的教学大纲的,只有一个NCTM(National Council of Teachers of Mathematics)Standards,这个标准对各个概念的教学要求都比较模糊,而且只是参考性质的,不强求。
当时不少教授的研究表明,新加坡日本的教材,其实比美国的反而更符合这个NCTM Standards,而且这些亚洲国家的大纲要求具体,条理明确,知识的进阶性也清晰。所以美国集合了一个数学教授和专家的委员会,参考亚洲这些数学先进地区数学大纲,综合了美国现有的数学教育研究成果,编了个美国版的,这就是Common Core。
说到这里,其实我很想建议,先把脑袋里关于common core的想法暂时抹去,去看看这个大纲的具体内容(注意,是去看common core大纲本身,不是common core的数学教材)。这个大纲是完全对大众公开的,内容在这里: http://www.corestandards.org/Math/ 点右边你想看的那个年级就可以了。其实每个年级的大纲内容没多少,几分钟就能看个大概。看完了你会发现,这大纲跟咱们小时候偷看的老师教参长得好像啊。
比如一年级里
Understand and apply properties of operations and the relationship between addition and subtraction.
CCSS.MATH.CONTENT.1.OA.B.3
Apply properties of operations as strategies to add and subtract.2 Examples:If 8 + 3 = 11 is known, then 3 + 8 = 11 is also known.(Commutative property of addition.)To add 2 + 6 + 4, the second two numbers can be added to make a ten, so 2 + 6 + 4 = 2 + 10 = 12.(Associative property of addition.)
就是要求能理解并运用加法交换律和结合律。
再比如
Represent and solve problems involving addition and subtraction.
CCSS.MATH.CONTENT.1.OA.A.1
Use addition and subtraction within 20 to solve word problems involving situations of adding to, taking from, putting together, taking apart, and comparing, with unknowns in all positions, e.g., by using objects, drawings, and equations with a symbol for the unknown number to represent the problem.1
就是要求能解答20以内的加减法应用题,包括添加和组合两种题型。
Common Core跟以前的教学要求最大的区别就是要求更具体了,比如说加减法的应用题(word problems)在以前是没有规定题型的,所以以前美国课本的应用题题型都很单一,加减法的应用题都是各种添加和减少;除法就是各种切蛋糕切pizza。但是Common Core把要求理解的题型增加了。比如加减法具体列出来三种(1和2是一年级要求,3是二年级要求):
1.添加和减少(小明手里三朵花,又摘了两朵,一共几朵?);
2.组合/两组合并/一大组分两组(小明摘了三朵红花,两朵黄花,一共几朵?);
3.比较(小明摘了三朵黄花,摘的红花比黄花多两朵,摘了几朵红花?)
再举个例子,对于加法,美国老师以前的做法就是数手指头,1+1数,4+5数,18+9数,5-2倒着数,12-4也倒着数,我以前做实验的时候,见过一个小朋友65-32也能倒着数出来!谁能自己想出来或者家里教简便算法,那算你运气好。
Common Core对于加法,继续参考亚洲参考科研书籍,要求小朋友得方法多样化,理解位值,会凑十,会利用Doubles(4+4=8, 6+6=12)推算出来简便算法。
每个年级对于运算和理解能力的进阶,都有明确具体的要求,不重复也不会过分拔高。
其实这些要求在那几个亚洲先进国家,还有中国的教学大纲里都是这么要求的,而且在美国的数学研究书籍里也是这么写的,只是一直没有被应用到课本编排里去。这么看来,Common Core应该挺靠谱的啊,怎么沦落到现在这种过街老鼠的地位了?
那是因为以上是原汁原味的Common Core, 就像这盘正宗的木须肉, 颜值如此,清清爽爽,条理分明,层次明确。

但是,食谱条理清楚,不代表你就能保证吃上一份原汁原味的作品。因为现实版的Common Core, 你看到和经历的是这么一盘黑乎乎看不清具体内容的美式木须肉。

完全是卖家秀和买家秀的差别。虽说Common Core本身内容没错,但是在实行方面,基本上所有该考虑的因素都没考虑到。
Common Core应用的受限因素
1
教材改编的结构
因为自己以前做教材对比研究的时候,接触过一些编写数学教材的人员。外加自家先生之前也在美国最大的出版社之一工作多年,跟不少教材出版人员打过交道。所以对这方面的了解是:即使大纲变了,写教材的还是同一伙儿人。而且编写教材任务繁重,很多内容都是根据新教材把原有的内容换个顺序,哪块缺了再补一块,任务急时间紧,根本没机会仔细研究。这么一来,新教材说是符合common core了,其实反而变得更杂乱无章,东补一块西补一块的凑数。只做到了覆盖大纲要求的内容,对小朋友的学习速度和理解能力的增长很少有深入的了解和考虑。
比如说,加减法的应用题,未知数在不同的位置(2+3=?和2+?=5,?+3=5,后两者难度大得多)在小朋友看来并不容易理解,但是书本里把这三题都归在同一个题型,一天就带过了。
课本编写人员的经验
之前说了,其实Common Core教材(教材不是统一的,很大出版社都有自己的教材)的编写人员跟以前的教材编写人员是同一拨人,(这也完全无法避免,否则哪儿能找到一批对common core有深刻理解的新人去?)所以他们对于新加的大纲要求,比如凑十,利用doubles,加法交换律,结合律这种以前很少明确要求的内容,也没有编写经验。写出来的东西水平参差不齐,可能有好的真能帮助学生理解相关概念的,也可能只是能勉强算上覆盖了大纲相关的内容,实际上写出来的题目和教学方法,并不真能够让学生理解。
这点真是美国教育机构的死穴,小学老师本来在本科阶段接受的专门针对数学教育的培训就少,就职之后的在岗培训和交流更少,突然空降一个对数学理解要求深入很多的大纲,别说教了,相当大的一部分老师自己都理解不了那么多题型和解题思路(参照马立平那本Knowing and Teaching Elementary Mathematics里美国老师对数学概念的理解)。所以很多概念和解题思路最多只能是勉强的照课本宣科,囫囵带过,并不能向小朋友解释清楚所以然。
举两个例子,
Common Core四年级的大纲里,要求用位值(place value)的概念去理解和运算多位数乘法。
CCSS.MATH.CONTENT.4.NBT.B.5
Multiply a whole number of up to four digits by a one-digit whole number, and multiply two two-digit numbers, using strategies based on place value and the properties of operations. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.
234*567里,小朋友应该理解:第一个数里的3乘以第二个数里的7,意思是30 (或者三个10)乘以7。这要求不过分吧?
再看看马立平书里对于中美小学数学老师的调查,其中有一道题就是举出小朋友做多位数加法的错误,请老师解释错在哪里了,应该怎么帮助小朋友改正。(出自书中第二章,28页)
92%的中国老师都认为小朋友的错误是因为对解题过程不理解(为什么要移位),对位值的概念不理解,应该针对这些概念的缺失去帮助小朋友改正错误。
但是只有30%的美国老师看出来这是问题的本质,其他的70%的美国老师都觉得是小朋友对公式的记忆错误,小朋友没记住应该每乘一轮往前移一位,所以改正方法应该是让小朋友熟记公式和解题过程。
这么一看,敢情Common Core的大纲要求,70%的老师都不理解?
再来一例难度稍微高点的,结果更吐血。Common Core的六年级大纲里要求,要会计算分数除法(一个分数除以另一个分数,也不一定非是特别刁钻复杂的分数),会根据一个分数除法的式子编个应用题,会以更直观的方式理解和解释分数除法。
CCSS.MATH.CONTENT.6.NS.A.1
Interpret and compute quotients of fractions, and solve word problems involving division of fractions by fractions, e.g., by using visual fraction models and equations to represent the problem. For example, create a story context for(2/3)÷(3/4)and use a visual fraction model to show the quotient;
也不过分吧?
再来看看马立平的研究,正好问到了中美数学老师这个概念(出自书中第三章,第55页)

结果呢?
只有43%的美国老师算对了这道分数除法。还不到一半!中国老师全部做对,而且好多老师还列出来好几种解题方法。
至于根据算式编应用题,所有参加的美国老师里,只有一个人编对了。其他人或者完全编不出来,或者编错的:把除以1/2,和除以2,还有乘以1/2完全搞混了。中国老师90%的编对了,还有好几个老师编了好几种不同情景的应用题。
也就是说,Common Core里对分数除法的要求,美国老师大部分自己都不会做,这怎么可能教会学生?(注:马立平这本书里都是血淋林的残酷数据,看之前最好先有心理准备,否则肯定郁闷。)
这两个例子只是现有研究里面抽出来的。至于大纲里每个学年要求的十几条知识概念的理解,美国老师自己能深切理解到什么程度,特别是对一题多解每个解题方法能不能理解贯通,并且给小朋友讲明白?这方面似乎怎么想都不容乐观。
最后,也是压死Common Core这骆驼的最后一根稻草
课本编不好,老师不会教,发回家的作业肯定需要家长辅导。可是这种连老师都不会教的,以美国大众的数学水平(咳咳),家长就能辅导了?肯定招来的只有家长的骂声一片啊。于是Facebook上贴满了对数学作业的批判,对Common Core的讨伐。
说实话这也真不能光怪家长,大壮现在一年级,有几次拿回来的作业,我看题目都看得一头雾水。因为那题目不仅没把Common Core的概念问清楚,课本的小编还自作聪明地给某些概念起了只有他们能理解的新的名字。家长把题目要求拿到手,完全不知道在问什么。就这样,一份条理分明,层次明确,进阶合理的大纲,被烹饪成了一份黑暗料理。
大纲原本的意图是引导小朋友从不同角度分析问题,用多种方法解题。但是因为教材设计和教师的原因,这些要求都无法向小朋友明白的解释清楚,也没有合理的练习结构和充足的时间让小朋友自己想清楚。
当然,写这篇文章的目的绝对不是为了让读者爸妈们郁闷得以头抢地的,我们得先了解情况,直面现实,才能更好的找到对策。
4 如何应对
在美国的华人妈妈常问的:那我们该怎么办?跟着学校教材走,一片混乱。另外找套好的教材(国内的或者其他亚洲国家的),又怕跟美国的大纲要求对不上,考试起来怕落了啥。
怎么办?三种方法
1)花重金找个教学过硬的私校(注:贵的私校并不保证等于教学过硬,教学水平得靠自己考察。而且,不少私校之所以学生成绩好,一大部分原因也是因为本来学生家长就是推妈推爸,在家里也自己教,跟学校的高要求相辅相成。所以也不能觉着只要进了高大上的私校家长就可以大撒手了)。
2)找家教(Tutor),一对一教学,最专注,价格没私校那么贵,不过也不便宜,一般来说一个小时$40-$60。当然家教的好坏还得自己挑,也有不少小学老师暑假时候兼职做家教的,不过如果在学校教不好的话,同一个人做家教就能教好?
3) 家里自己开小灶,优点:额外开销小,时间灵活,一对一针对性强。但是,也需要家长投入时间和精力,如果只是想帮助小朋友把需要学的内容学透的,而不是系统性的把小朋友教成比现在年级高一两年的水平,而且投对了方向和方法的话,其实需要时间并不会太多。家长得先了解教学要求和方法。
因为1和2 都是花钱买人家的服务,就不用多说了。这里具体说的是3,估计也是大多数群众会用的方法。
-
了解小朋友那个年级的数学教学要求。怎么了解呢?解铃还须系铃人,回到Common Core (http://www.corestandards.org/Math/)。 之前说过了,这个大纲本身挺靠谱的,而且内容也不繁杂,每个年级需要掌握哪几项概念,网站上列得很清楚,每个年级的内容其实就一两页,看一遍不会太花时间。清楚了本学年的教学要求,那么无论是用国内的教科书,或者新加坡数学,或者美国其他教科书,或者练习册和IXL之类的题库,都能从中挑出来家里小朋友需要加强学习的内容。
-
小朋友学数学,需要在两方面下功夫:理解和熟练。
-
理解:要做到理解,要抓住时间抓住机会,也就是“教育契机”,趁小朋友头脑放松,感兴趣的时候,结合当时的场景来解释概念。
比如一起买菜、做饭、烤蛋糕这些时候,小朋友全情投入跟爸妈一起干活或者亲子活动,随口聊个话题把数学编进去,注意力和脑袋的转速肯定比平时做作业高。(MingMath 的 Facebook page, https://www.facebook.com/MingMath/,每个星期都会有一小篇超市数学,专门介绍如何在买菜的时候,简单的利用超市的环境和信息,向小朋友介绍数学概念)。当然,能这种随时抓机会的前提还是回到第一条,了解本年级的教学要求,所以,先读大纲很重要!
举个例子,大壮学校的教材就是根据CC编制的,每个月会给家长发两张Home Link向家长说明下个月的教学内容和目标。
开学第二个月的家长单里,列出的学习内容为加法,包括利用数实物,数轴,十点框(ten frame)计算加法,加法的交换律和结合律,还包括以增加和组合作为大背景的两大类加法应用题,并且包括把未知数放在加法等式中三个不同位置的题目。
这么一大堆东西,会在四个星期不到二十个课时里,每天讲一种,然后每天会有个5分钟的作业,来巩固练习。这么大面积的蜻蜓点水教学法,稍微想一想就会觉要想让小朋友能真正理解,完全是mission impossible。
其实这些内容确实是大纲里的要求,对小学一年级的学生也是合理要求,只是教学太表面化,太受时间限制了。
所以做为家长,咱们既然能从大纲里知道这些要求,完全可以在这整个学年里,慢慢通过身边的情景,通过教育契机给小朋友时不时地讲解这些概念。当小朋友有机会反复接触这些概念,再融合到他们日常对数的理解中,对这些概念就不会停留在蜻蜓点水的层了。
按照中国的小学数学课本,小朋友学习数字11-19的时候,这个概念就被反复洗脑很长时间。之后学多位数的加减乘除法的时候也是不断洗脑位值。
可惜美国的教学,位值只是蜻蜓点水的一两节课,而且这一两节课,还不光是介绍十进制,还有走马观花的三进制五进制。
很多老师只是把位值当成一个独立的小知识点,而不会把它重视成其它运算的基础。当再介绍其它运算,就像之前提到的那个中美老师分析多位数除法的运算错误一样,对加减乘除的竖式计算只当成是一个要记住的公式,算错了就是因为公式没记清楚,而不会追究到位值的理解,所以很多情况下只会要求治标不治本的背公式,后患无穷。
既然学校重视得不够,只能家里多洗脑。多位数加减法学得迷糊的,只要把位值搞清楚,问题就解决90%。( https://www.facebook.com/MingMath/上正在连载一系列的利用家居小用品,教小朋友位值概念的教学录像)
最后再回到Common Core的话题上来。虽然这个大纲在美国的执行是注定是困难重重几乎不可能成功的,但只要咱们做父母的稍微花多一点点时间,以咱们华人父母的数学功底(别忘了,中国初中毕业生的平均数学水平,都高于美国小学教师的平均数学水平),加上Common Core本身内容跟咱们小时候的数学大纲的高度相似,只要能按照大纲里的基本教学要求,帮助小朋友提高相应概念的理解和计算的熟练度,小朋友的数学还是可以学的扎实深透的。

















