根据爱因斯坦在 1915 年提出的广义相对论,引力源于时间和空间(二者合并为四维的时空)的几何结构;任何有质量(或能量)的物体都会使时空弯曲。比如,在地球质量作用下,苹果树顶端的苹果的时间,要比在树下工作的物理学家的时间流逝得更快一些。苹果从树上落地,其实只是对时空弯曲的反应。这种时空弯曲使地球在轨道上绕着太阳转动,也使遥远的星系进一步离我们远去。这一惊人而美妙的想法已经被很多精确的实验证实。
用时空几何的弯曲来取代引力相互作用的理论取得了巨大的成功,科学家自然地想到,能否找到一种几何化的理论来解释自然界其他基本相互作用,乃至基本粒子的种类?对这个问题的追寻耗尽了爱因斯坦的后半生,而特别吸引他的是德国科学家西奥多·卡卢察(Theodor Kaluza)和瑞士科学家奥斯卡·克莱因(Oskar Klein)的工作。基于引力反映了四维时空的几何结构这个想法,他们进一步提出,电磁相互作用其实来自于一个额外的空间维度(即第五维)的几何结构,而这一维度因为太小目前无法被任何实验直接探测到。爱因斯坦对这个统一理论的追求以失败告终,因为当时的条件还不成熟。要想统一基本相互作用,首先要理解核力以及量子场论在基础物理中的关键作用,而物理学家直到 20 世纪 70 年代才弄明白这些。
时至今日,对统一理论的追寻已经成了理论物理的核心问题之一。而正如爱因斯坦预计的那样,几何概念在其中扮演了重要的角色。在弦论这个最有希望统一量子力学、相对论和粒子物理的理论框架中,卡卢察和克莱因的想法重新受到重视和推广,并成为弦理论的基本特征之一。在弦理论以及 Kaluza-Klein 猜想中,我们看到的物理定律是由这些额外的微观空间维度的形状和大小决定的。但又是什么决定了它们的形状呢?最近几年,理论和实验的一些进展提供了一个惊人而又充满争议的回答。如果正确,这一回答将极大地改变我们对宇宙的理解。
Kaluza-Klein 理论和弦
在 20 世纪早期,卡卢察和克莱因提出第五维度的概念时,物理学家只知道自然界两种基本的力:电磁力和引力。这两种力都与相互作用距离的平方成反比,所以科学家自然地猜想,它们之间是不是有某种联系。卡卢察和克莱因注意到,如果存在一个额外的空间维度(从而使时空成为五维),爱因斯坦把引力几何化的理论或许可以把它们联系起来。

图片来源:http://www.diffusion.ens.fr/vip/tableJ02.html
这样一个额外维的想法并没有看上去那么疯狂。因为如果额外空间维度蜷曲成一个足够小的圈,那么我们最好的“显微镜”——能量最高的粒子加速器也无法看到它。不仅如此,从广义相对论中我们已经知道,空间并不是绝对的,而是会扭曲和演化的。比如我们今天可以看到的三个空间维度一直在膨胀,在遥远的过去它们的尺度都很小,所以如果还有额外的维度没有膨胀,从而到今天都保持微观的尺度,似乎也可以理解。
尽管我们无法直接观测到额外维,它仍然可能有重要的、非直接的效应可以被我们观测到。如果有一个额外维,广义相对论可以直接描述整个五维时空的几何结构,这一结构可以分为三部分:大尺度四维时空的形状、小尺度额外维和四维时空之间的角度,以及额外维蜷曲的周长。四维时空由通常的四维广义相对论描述;其中每一点上,额外维的角度和周长都有特定取值,就像是两个在时空中每一点都有取值的场。令人惊讶的是,角度场模拟了四维时空中的电磁场,即该角度场满足的方程和电磁场满足的(麦克斯韦)方程组完全相同。另一方面,周长场决定了电磁力和引力之间的相对强度。因此,从五维引力理论出发,我们得到了四维时空中的引力和电磁力理论。
存在额外维度的可能性,在追求广义相对论和量子力学统一的过程中,也已经起到了关键的作用。在目前最领先的弦论中,基本粒子其实是一维物体,即很小的、振荡的弦。弦的尺度接近所谓的普朗克尺度,即 10-33 厘米(比原子核直径的一百亿亿分之一还要小)。因此,从任何比普朗克尺度大得多的尺度上看,弦都完全像一个点。
为了使弦论的方程在数学上自洽,弦必须在 10 维的时空中振动,这也意味着存在额外的 6 个空间维度,因为尺度太小还无法被探测到。和一维的弦类似,时空中还存在各种维度的“膜”。在原始的 Kaluza-Klein 理论中,普通粒子的波函数可以充满额外的维度,因此粒子本身必然扩散到所有额外维度。与之不同的是,弦可以被限制在某个膜上面;而且弦论中也可以有所谓的通量,即由“场线”表示的力场,正如经典电磁学中可由“场线”表示的电磁力一样。
总的来说,弦论中额外维的图景比 Kaluza-Klein 理论要复杂一些,但背后的数学结构更加统一和完备。Kaluza-Klein 理论的中心思想并没有变,即我们看到的物理定律取决于隐藏的额外维的几何结构。
太多的解?
关键问题是:什么决定了额外维的几何结构?广义相对论的答案是,时空几何必须满足爱因斯坦场方程——用普林斯顿大学的约翰·惠勒(John Wheeler)的话说,物质告诉时空如何弯曲,时空告诉物质如何运动。但爱因斯坦场方程的解不唯一,因此有大量可能的时空几何。五维的Kaluza-Klein理论提供了这种不唯一性的一个简单例子。蜷曲的额外维的周长原则上可取任意的值:在没有物质的情况下,平坦四维时空,加上一个任意周长的圆圈,都是爱因斯坦方程的解(在有物质的情况下,类似的场方程也存在多个解)。
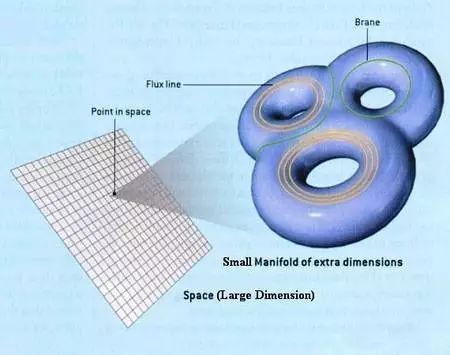

弦论方程的任何一个解都代表了时间和空间的一个位形,这个位形包括隐藏维度的排列方式,还有与之相关的膜(绿色)和通量线(也称力线,橙色)。弦论预言我们的世界有六个额外的维度,所以在我们熟悉的三维空间中的每个点中都隐藏着一个六维的空间,或者说流形(manifold)。在三维空间看到的物理规律取决于这个六维流形的尺度和结构:有多少个多纳圈一样的把手、每个把手的长度和周长、膜的数量和位置,以及围绕每个多纳圈的通量线的数目。
图片来源:http://lesmerveillesdelaconnaissance.over-blog.com/article-dossier-la-mysterieuse-energie-noire-partie-1-73205896.html
在弦论中,我们有多个(6个)额外维,从而有多得多的可调参数。一个额外维只能以圆圈的方式蜷曲起来;但当存在多个额外维度时,它们可以有各种不同的形状(更准确的说,有不同的“拓扑”),例如一个球面,一个多纳圈,两个粘在一起的多纳圈,等等。每个多纳圈(即一个“把手”)都有各自的长度和周长,从而为额外维搭配出大量不同的几何结构。除了这些“把手”还有其他参数,例如膜所在的位置以及绕着每个圈的“通量”数目等。
尽管如此,这些不同解的贡献有很大的差别:由于额外维中的通量、膜以及空间曲率都会贡献能量,每个解都有相应的势能。我们把该能量称为真空能,因为这是在大尺度的四维时空中完全没有物质和场的情况下,时空本身的能量。正如一个放在斜坡上的球会向着最低处滚动下去,额外维的几何结构也会向着真空能最低的方向演化。
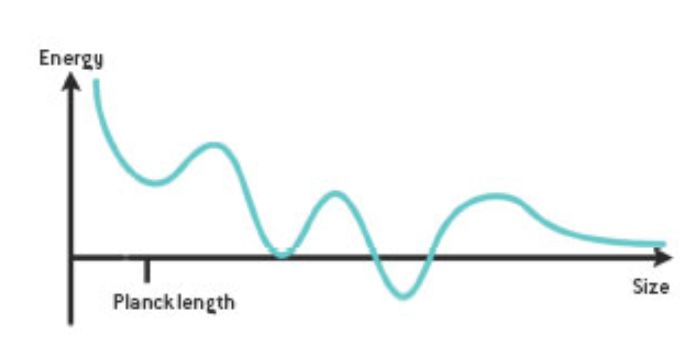
为了理解真空能最小化这一过程的后果,我们先考虑一个参量,即隐藏的额外维的总大小。我们可以画出真空能随着这一参数变化的曲线。上图显示了这样一个曲线的例子。在额外维很小的情况下,真空能很高,所以在图的左侧,曲线是从比较高的位置开始的。从左向右,真空能先后到达过三个山谷,每个都比前一个更低。最终,在图的右侧,曲线慢慢下降到一个常数。这里最左边的山谷的真空能数值是大于 0 的,中间那个山谷真空能恰为 0,而最右边那个山谷真空能小于 0 。
隐藏的额外维的几何结构如何演化还取决于初始条件,即“球”一开始处于曲线的哪个位置。如果演化开始于最后一个顶峰的右侧,球会一直滚到无穷远,也就是说额外维的尺度会无限增加(因此将不再是隐藏的)。否则的话它会停止在某个山谷的最底部,隐藏的额外维尺度会调整到使能量最低的值。这三个局部的最低点分别对应真空能为正、为负和为零的情况。注意我们宇宙的额外维尺度没有随时间变化,否则的话我们会看到自然基本常数随时间变化。因此我们的宇宙肯定正处于某个山谷的底部,而且应该是处于一个真空能稍大于零的山谷。
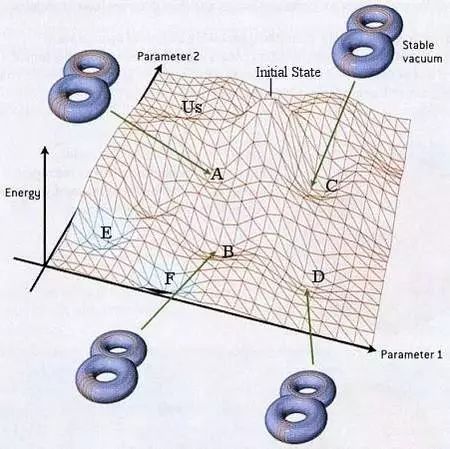

真正的弦论景观反映了额外维流形所有的参数,因此形成了一个维度非常多的“地形图”。这个地形图只画出了依赖于两个变化参量的真空能。额外维流形依然会倾向于处在某个谷底(对应一个稳定的弦论解,或者说稳定的真空)。换句话说,一旦流形处于谷底了,它就倾向于长时间停留在那里。图中蓝色的部分表示小于零的真空能。 但是,量子效应允许一个流形在某个时刻突然改变状态——即通过量子跃迁穿过中间的山脉,到附近一个更低的山谷。宇宙的不同区域会在景观中走随机的不同路线。这个结果就像是无数个探险者在整个景观中探索,从而经过了所有可能的山谷。
图片来源:http://lesmerveillesdelaconnaissance.over-blog.com/article-dossier-la-mysterieuse-energie-noire-partie-1-73205896.html
因为额外维的几何结构有多个参数,我们应该把刚才这个真空能曲线看成某个复杂的高维“山脉”的一个切面。斯坦福大学的伦纳德· 萨斯坎德(Leonard Susskind)把这个“山脉”称为弦论的“景观”。这个高维的“景观”的各个最小值——即球会最终停留的谷底,对应于时空几何的稳定位形(包括膜和通量的位形);我们将这些位形称为稳定真空。
一张现实中的地形景观图只有两个独立方向(南北和东西),我们只能画出二维的景象。而弦论的景观要复杂得多,有很多(数百个)独立的方向。我们不应该把弦论景观的维度和空间的维度混淆起来;每个独立方向量度的不是物理空间中的某个位置,而是时空几何的某个方面,比如“把手”的大小或者膜的位置等。
目前我们还不能完整地描绘整个弦论的景观。计算一个真空态的能量是个困难的问题,而且通常需要做某种适当的近似。近年来理论物理学家开始取得了一些进展,特别是在2003年,斯坦福大学的沙米特·卡奇鲁(Shamit Kachru)、雷纳塔·考洛什( Ren-ata Kallosh)和安德烈·林德 (Andrei Linde),以及印度塔塔基础科学研究院(Tata Institute of Fundamental Research)的萨迪普·特里维迪(Sadip Trivedi)发现了很有说服力的证据,证明弦论景观确实存在山谷,在这些山谷中我们宇宙的基本性质是稳定的。
我们还无法确定有多少稳定的真空——即有多少个点可以让“球”停住,但这个数字很有可能是无比巨大的。有研究表明,可以有带 500 个左右“把手”的解,把手数目不会比这个数字大太多。对每个把手,可以有一定数目的通量线绕着它;这个数目不会太大,否则它们会导致真空不稳定。如果我们假设每个把手可以有 0 到 9 条可能的通量线(10 种可能),那么总共 500 个把手对应 10500 种可能的位形。即使每个把手只有 0 或 1 条可能的通量线,也有大约 2500(大约 10150 )种可能性。
除了影响真空的能量外,这些解中的每一个,都会在我们四维的宏观世界导致完全不同的现象:定义我们世界有哪些种类的粒子和相互作用,以及它们有怎样的质量和强度。尽管弦论可能提供了唯一的基本定律,我们在宏观世界中看到的物理定律仍然会依赖于额外维的几何结构。
很多物理学家都希望,物理学最终可以解释为何宇宙要有这样一些特定的基本法则。但即使这个愿望成为现实,仍然有很多关于弦论景观的深刻问题需要回答。哪一个稳定的真空描述了我们的宇宙?为什么自然选择了这一个特定的真空而不是别的?其他稳定的解是否只是纯粹数学上的可能性,而永远不可能成为物理现实?如果弦论是正确的,似乎它无法实现最终的“民主”:尽管理论上有大量的可能的世界,最终在所有可能之中却只挑出了对应我们现实世界的那一个。
是否必须要在弦论景观中挑出一个特殊解呢?根据两个重要的想法,我们在 2000 年提出了一个完全不同的图景。第一个想法是,我们的世界不必永远处于一个弦论解(或者说额外维的位形),因为有罕见但可以发生的量子过程允许额外维从一种位形跳到另一种。第二个想法是,根据作为弦论一部分的爱因斯坦的广义相对论,宇宙可以演化得足够快,从而允许多个不同位形共存于不同的“子宇宙”中,而这些子宇宙每个都足够大,以至于在其中无法观测到其他宇宙。在这个图景里,为何真实存在的唯有我们世界对应的那个真空的谜团,就不存在了。不仅如此,我们进一步提出,这个想法还可以解决另一个重大的自然谜题。
景观中的一条路径
正如前面提到的,每个稳定的真空都可以由“把手”的个数、膜和通量的数目来描述。但现在我们要考虑到,这些要素都是可以被创造和毁灭的,因此在一段时间的稳定期之后,我们的世界可以跳到一个完全不同的位形。在弦论景观里,一个通量线的消失(衰变),或者其他形式的拓扑改变是穿过“山脉”进入更低的一个山谷的量子跃迁。
这样的后果是,随着时间的演化,不同的真空都可以依次存在。假设一开始我们例子里的 500 个把手每个都有 9 个通量,一个接一个,这 4500 个通量会按照量子力学预言的某种顺序依次衰变,直至所有通量都用完。我们从景观中较高的山谷出发,经过一系列随机的跃迁,经过了 4500 个越来越低的山谷。我们在弦论景观中看到了一系列不同的风景,但对于 10500 种可能的真空来说,这一过程只经过了极小的一部分。似乎大多数真空连个露脸的机会都没有。
但其实我们忽略了这个故事中的一个关键部分:真空能对宇宙演化的重要效应。我们知道,通常物质(比如我们的恒星和星系)会让宇宙的膨胀减缓,甚至最终导致其重新塌缩。但正的真空能起到的效果则像是反引力一样:根据爱因斯坦场方程,它会导致我们的三维空间以越来越快的速度膨胀。当隐藏维通过量子效应跃迁到一个新位形时,这一加速膨胀会产生重要而令人意外的效果。
由于三维空间中的每个点都隐藏着一个六维空间,而这个六维空间对应着弦论景观中的一个点。当这个六维空间跃迁到一个新位形的时候,这个跃迁并不是在三维空间中的所有地方同时发生的。跃迁首先在三维宇宙中的某个点发生,而这个新的、能量更低的位形周围形成了一个泡泡,这个泡泡迅速膨胀。如果三维空间没有在膨胀的话,这个迅速膨胀的泡泡会最终占据宇宙中的每个点。但是,旧的区域也在膨胀,而且有可能比这个新的泡泡膨胀得更快。
大家都是赢家:旧的和新的区域都增大了,所以新的区域永远不会完全毁掉旧的区域。根据爱因斯坦的理论,时空几何结构是动态变化的,因此这样的情况完全可能出现。广义相对论不是一个零和游戏:空间构造的扩张使得旧和新的真空都有更多空间被创造出来。类似的过程在新真空“变老”的时候也会发生。当新真空开始衰变的时候,它并不会彻底消失,而是在内部长出另一个真空能量更低的、不断膨胀的泡泡。
由于旧的区域也在增长,最终真空会在另一个地方发生衰变,而跃迁到弦论景观中另一个附近的山谷。这个过程会继续发生无数次,以所有可能的方式衰变,而相距足够远的区域会在不同的把手上失去通量。因此,宇宙不再只是经历了单个衰变的序列,而是经历了所有可能的序列,最终的结果是成为泡泡套着泡泡的多重宇宙。这个结果和麻省理工学院的艾伦·古思(Alan Guth),塔夫茨大学(Tufts University)的亚历山大·维连金( Alexander Vilenkin) 以及林德的永恒暴胀理论得到的结果很类似。


我们提出的这个图景可以比喻成,有无数个探险者去探索图景中每种可能的路径,经过了所有的山谷。每个探险者代表宇宙中的一个点,而它们互相远离。每条探索的路径代表了宇宙中这个点经历的一系列真空。只要该探险者在图景中开始的点足够高,实际上所有的山谷都会被探索到。事实上,每个山谷都会被来自更高处山谷的每条可能路径穿过无穷次。这个“瀑布”一般的下降过程只有到“海平面”才停止——即当真空能变为负的时候。负的真空能对应的时空几何结构不允许这种无穷膨胀和泡泡继续形成。与之相反,一个局部的“大塌缩”将会发生,就像黑洞内部的过程一样。
在每个泡泡里,一个在足够低的能量下做实验的观察者(正如我们一样)将会看到一个有自己特定物理规律的四维宇宙。观察者无法获取来自其泡泡之外的信息,因为泡泡之间的空间膨胀太快,以至于光速也无法跑赢它。观察者之所以只能看到自己这个真空对应的物理定律,是因为看得不够远。在我们这个图景里,我们宇宙的起源(即宇宙大爆炸的开始)不过是我们附近某个位置最近发生的一次真空跃迁,而如今这一泡泡已经膨胀到几百亿光年的大小了。遥远未来的某一天(遥远到我们应该不需要担心),宇宙的这个部分可能会经历又一次跃迁的过程。
真空能危机
我们刚刚描述的这个图景解释了弦论景观中不同的稳定真空是怎样在宇宙中的不同位置出现,从而形成了无数个“子宇宙”的。这一结果也许将解释理论物理中最重要也是最难解决的问题之一——真空能问题。对爱因斯坦来说,我们刚刚说的真空能其实只是广义相对论场方程中大小任意的一项,即所谓的“宇宙学常数”——为了与他所相信的宇宙静止这一观念一致,他曾经在方程里加了这一项。为了得到静止宇宙,爱因斯坦要求宇宙学常数是一个特定的正值,但当后来的观测证明宇宙在膨胀之后,他又抛弃了这一想法。
有了量子场论之后,曾经被认为是虚空的空间(即真空)变成了热闹的地方:这里充满不断产生和湮灭的虚粒子和场,而且每个粒子和场都带有正或负的能量。基于量子场论的一个很简单的计算表明,这些虚粒子的能量达到了一个极高的能量密度:大约每立方厘米 1094 克,也即每普朗克体积(即普朗克长度的 3 次方)有一个普朗克质量。我们把这个能量密度叫做 ΛP。这一计算结果被称为物理学史上最著名的错误预言,因为实验观测很早就告诉我们真空能肯定不会超过 10-120 ΛP。理论物理因此陷入了一个巨大的危机。
为什么理论和实验之间会存在巨大分歧?过去几十年,搞清楚这个问题一直是理论物理的中心目标之一,但物理学家提出的无数个解决方案中没有一个得到广泛接受。很多方案都假设真空能是严格为零的——考虑到我们要得到一个小数点后面至少有 120 个零的数字,这显然是一个很合理的假设。因此我们的任务就是要解释物理学为何能得到一个严格为零的真空能。很多尝试都基于一个设想,即真空能可以将自己调整为零,但目前并没有令人信服的解释告诉我们这一调整如何发生,以及为何结果很接近零。
本文作者在 2000 年发表的一篇文章中提出了一个解释,我们利用了弦论大量的解和其宇宙学意义,并把它们与得克萨斯大学奥斯汀分校的史蒂文·温伯格(Steven Weinberg)在 1987 年提出的一个想法结合起来。
首先考虑弦论的大量解。真空能可以看成是这些解在弦论景观中对应的点的海拔。海拔的范围可以从最高点对应的 ΛP 一直到最低点对应的 -ΛP。假设弦景观一共有 10500 处山谷,它们的海拔可以是这两个极端值之间的任意值。如果我们把这些解画出来,并用纵轴代表它们的海拔,那这些山谷在纵轴方向的平均间隔就该是 10-500ΛP。因此,我们会看到很多解的真空能是在 0 和 10-120ΛP 之间的,尽管它们只占总量的很少一部分。这一结果解释了怎样能得到很接近零的真空能。
这个想法并不是全新的。早在 1984 年,已故的苏联物理学家安德烈 ·萨哈罗夫 (Andrei Sakharov)就提出,额外维的复杂几何结构也许可以使真空能的取值处于实验观测范围内。另外一些研究者也提出过一些似乎不依赖于弦论的解释。

图片来源:http://news.qudong.com/article/324383_2.shtml
至此,我们就解释了宇宙演化是怎样实现弦景观中绝大部分稳定解的,其结果是一个很复杂的、有大量泡泡的宇宙,泡泡对应的真空能可以取遍所有可能的值(包括很接近零的那些)。但问题是,我们的宇宙处在其中哪个泡泡里?为何我们宇宙的真空能如此接近于零?这里我们就需要借助温伯格的想法了。当然这里有概率的因素,但因为很多地方是完全不适宜生命存在的,所以我们没有“生活”在那些地方并不是一件奇怪的事情。这其实是一套我们很熟悉的逻辑了,就像一个人不太可能出生在南极或者马里亚纳海沟或者没有空气的月球上。与之相反,我们发现我们生活在太阳系中这一极小的、适合生命生存的部分。同样的道理,只有很小的一部分稳定真空是适于生命存在的。宇宙中那些有比较大的、正的真空能的区域会发生极其剧烈的膨胀,与之相比,超新星爆发简直可以用平静一词来形容。而有较大的、负的真空能的区域会以很快的速度消失在一次宇宙塌缩中。如果我们所在的泡泡的真空能大于 10-118ΛP 或者小于 -10-120ΛP,我们将不可能存在,正如我们不会存在于温度太高的金星或者重力太大的木星上一样。这种逻辑通常被称为人择(anthropic)原理。
弦论景观中有大量的山谷是处在适宜范围内的(海平面向上或向下不超过一根头发丝直径的范围)。因为我们这样的生命存在,我们所在的泡泡的真空能很小并不奇怪。但我们同样也没有任何理由期待它刚好是零。大概有 10380 种真空是在适宜范围内的,但只有极小一部分的真空能会严格为零。如果真空的分布是完全随机的,那么 90% 的真空分布于能量在0.1x10-118 到 1x10-118ΛP 这一范围内。所以如果弦论景观这个图景是正确的,我们应该会观测到非零的真空能,而且其数值很可能不比 10-118ΛP 小太多。
对遥远的超新星的观测表明,可观测到的宇宙正在加速膨胀——这是实验物理历史上最令人震惊的发现之一,也是我们的宇宙具有正的真空能的重要证据。从宇宙加速膨胀的速率可以推出,真空能的数值大约就是 10-120ΛP——这一数值足够小,以至于其他实验无法探测到;但又足够大,可以符合人择原理的解释。
因此,弦论的图景似乎解决了物理学的真空能危机,但这一解释也有一些令人不安的后果。爱因斯坦曾经问过,上帝在创造宇宙的时候是否有选择的余地,还是说宇宙的定律已经完全由一些最基本的原理确定了。作为物理学家,我们也许期待的是后一种情况。尽管我们还没有完全理解弦论背后的基本原理,但似乎这些原理是完全确定且不可避免的——因为其背后的数学不允许我们有任何选择。但是,我们所能看到的这个世界的物理定律并不是基本原理,而是取决于有无数种选择的额外维几何结构。我们所看到的一切并不是必然存在的,它只是依赖于我们居住在某一特定泡泡里这样一个事实。
除了可以自然地给出很小但非零的真空能之外,弦论景观能否给出其他预言呢?要回答这个问题,我们需要对真空的能量分布有更深的理解,而这也是一个涉及多个研究前沿的很热门的领域。不仅如此,目前我们还没能找到一个特定的稳定真空,它的物理定律和我们这个四维时空里的完全一致。总的来说,弦论景观基本上还是个没怎么被探索的领域。在这个问题上,物理实验可能会给我们提供帮助。也许某天,我们能够直接在加速器上看到弦、黑洞或者 Kaluza-Klein 理论里的新粒子,从而直接看到高维的物理定律。又或许我们可以直接通过天文观测,看到宇宙学尺度上的弦,这些弦有可能在宇宙大爆炸开始时就被创造出来,一直随宇宙膨胀而变大。
我们给出的这整个图景其实是很不确定的。目前我们还没有一个可以与广义相对论媲美的、精确而完整的弦论体系。广义相对论拥有建立在已经得到充分理解的物理原理之上的精确方程;而对于弦论,目前我们还不清楚它的精确方程,还有可能尚未发现某些重要的物理概念。如果搞清楚了这些,我们这里讲的弦论景观,包括形成泡泡的机制,可能会完全改变,甚至被推翻。在实验方面,从宇宙学观测的结果来看,非零的真空能几乎是一个确定的结论了,但我们也知道,宇宙学的数据是“善变”的,所以也许还会有令人惊奇的新发现。 当然,也许其他理论也能解释一个非零而又极小的真空能,现在就停止寻找,显然为时过早。但同样,我们也不能完全排除弦景观图景——也许我们真的身处一个丰富多变的宇宙中的一个宜居角落。
本文作者 拉斐尔·布索和约瑟夫·波尔金斯基的这篇文章始于在圣巴巴拉召开的一次关于弦论对偶的研讨会。文章结合了布索在量子引力和暴胀宇宙学方面的知识和波尔金斯基在弦论方面的知识。布索当时是加利福尼亚大学伯克利分校的助理教授,他的研究方向主要是联系时空几何和信息的全息原理。波尔金斯基当时是加利福尼亚大学圣巴巴拉分校科维理理论物理研究所的教授,他第一个发现了膜在弦论中的重要地位。
本文译者 何颂是中国科学院理论物理研究所副研究员,主要研究方向为量子场论、弦论、数学物理。
相关阅读 《弦论》是怎样诞生的 | 理论物理学家约瑟夫•波尔钦斯基回忆录译文节选

























