在6个人当中，无论他们之间的关系如何，必定有3个人互相认识，或者3个人互不相识。

如果用图论的方法来思考，可以这么证明：

假设两个人之间如果互相认识，就用蓝色线连起来，如果彼此不认识，就用红色线连起来，那么无论怎么连线，必然能在6个点中连出三边同色的三角形。

假设两个人之间如果互相认识，就用蓝色线连起来，如果彼此不认识，就用红色线连起来，那么无论怎么连线，必然能在6个点中连出三边同色的三角形。

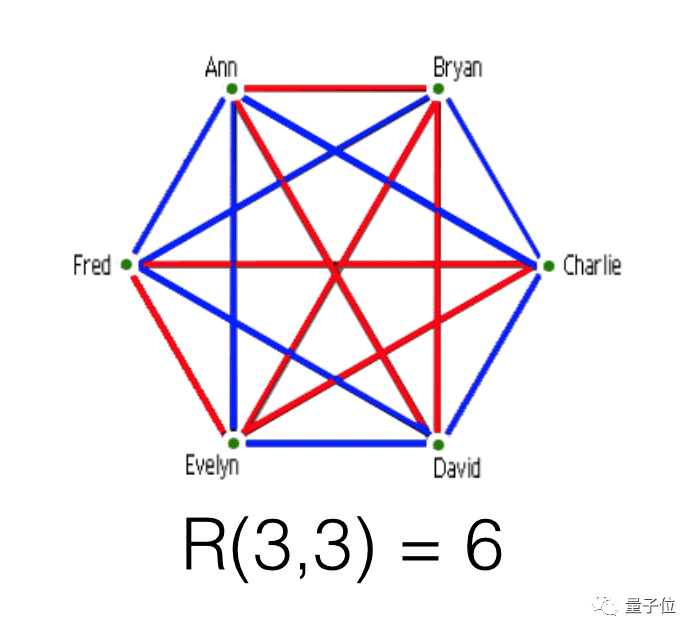
但如果只有5个人的话，很快就能找到一种连不出同色三角形的方法。

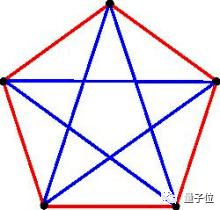
小于5的数，也能被用同样的方法证明不符合这一结论。

现在，就可以引出拉姆齐数的定义了：

找一个最小的自然数R（k,l）=n ，使得n个人中必定有k个人互相认识或l个人互不相识。

找一个最小的自然数R（k,l）=n ，使得n个人中必定有k个人互相认识或l个人互不相识。

其中，n就是拉姆齐数。

也就是说，R（3,3）=6，这里的6就是拉姆齐数。

看起来拉姆齐数似乎并不难找，但当顶点数稍微增加一点时，求解拉姆齐数的难度却会大大增加。

1930年，拉姆齐本人求出R（3,3）=6，1995年，数学家把求解推进到R（4,5）=25，至于R（5,5）是多少，数学家到现在也不知道，只知道它介于43到48之间。

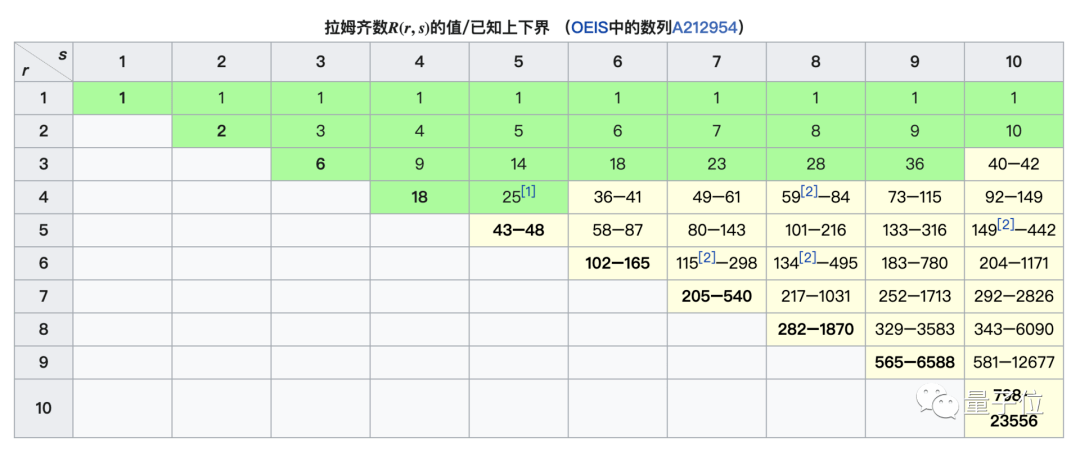
这是为什么呢？

想象一下，要连线的顶点数从6个变成了40个，哪怕只用2种颜色随机在两点间连线，也有2 780 种方法。

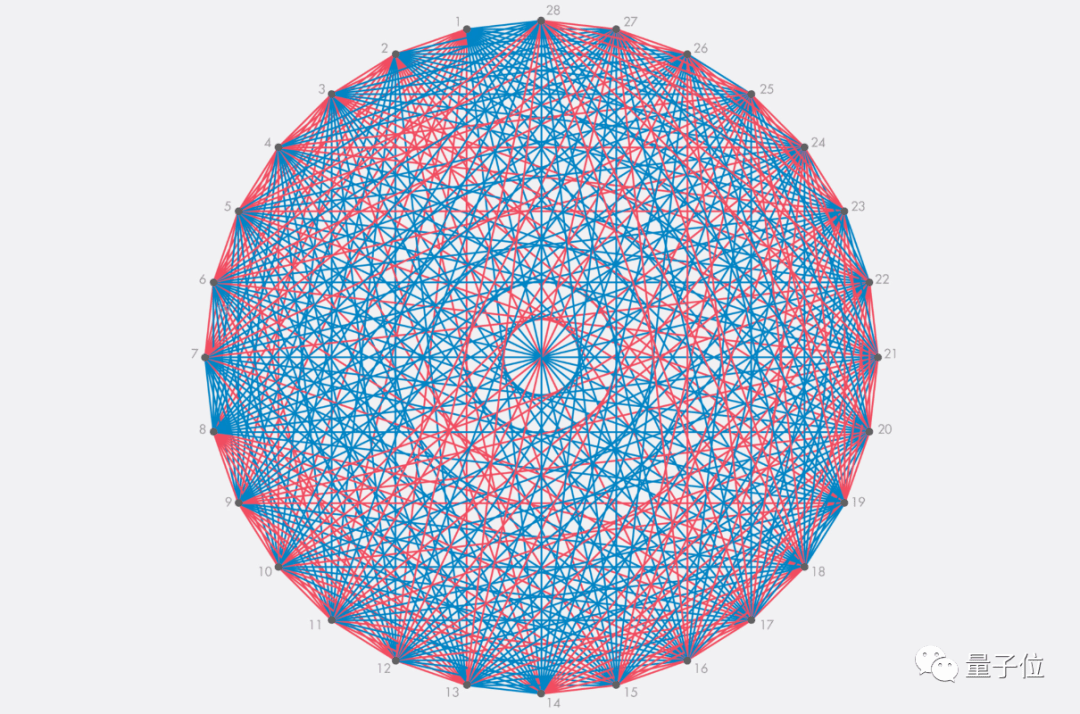
△28个顶点，连一次线就已经达到这种密度

换算下来，就是要进行 6.35×10 234 次连线判断，对比宇宙中所有的粒子总数，也不过3.28×10 80 个。

这还只是2种颜色的情况，至于3种颜色、4种颜色……

要在这么多种连线的组合里，找到5个点两两相连是否必然存在的情况，几乎是不可能做到的事情。

虽然无法求出拉姆齐数的准确值，但是数学家们一直在想办法限制其范围。

对于R（5,5）来说，其上限和下限分别就是48和43。

从1930年起，就有科学家开始研究拉姆齐数的上下限的公式，来缩小拉姆齐数的范围。

著名数学家保罗·埃尔德什研究了几十年，得到了一个著名的上下限公式：

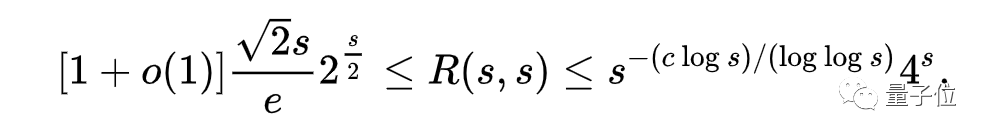
然而这个范围还是不够小。

Ashwin Sah在今年5月提出的证明方法，基于2009年Conlon的论文进行了改进，并提出了两种颜色的拉姆齐数的新上限。

论文给出的推论，被许多业内人士认为是使用现有研究线索可以获得的 最佳结果。

他给出的上限计算公式，对于R（4,4）以上的拉姆齐数都有效。

目前这一论文所采用的方法，已经被少数数学家进行了优化。

对此，David Conlon教授表示：

他将这种方法推理到了极限。

他将这种方法推理到了极限。

能被开创这种方法的作者给予如此高度的评价，也说明了Sah所完成工作的难度和前沿性。

10月29日，专门针对美国、加拿大和墨西哥大学生 在数学领域表现优异的摩根奖，授予了Sah和另外一名学生Mehtaab Sawhney，以表彰他们本科时期在离散数学、概率等领域作出的贡献。

相较于同龄人，在本科阶段就能达到这样的数学水平，也与Sah的成长经历密不可分。

从小展露数学光芒

除了自身的天赋外，Sah一直保持着对数学的钻研精神。

外媒Quantamagazine给予他这样的评价：

A Life of Math.

A Life of Math.

这不仅仅是基于他在近期取得的成就，而是从小就与数学结下了的不解之缘。

Ashwin Sah出生在美国俄勒冈州的波特兰市，他在回忆儿时情节时表示：

我现在比较印象深刻的儿时记忆，是妈妈在教我一些基本的算术。

我现在比较印象深刻的儿时记忆，是妈妈在教我一些基本的算术。

△11岁的Ashwin Sah在做数学题

2016年夏天，年仅16岁的他，便在香港举办的国际数学奥林匹克竞赛 （IMO）中，斩获金牌。

可以说，Ashwin Sah在一次次的竞赛中，「品尝」到了高等数学的魅力。

紧接着第二年，也就是在17岁的年纪，他便顺利进入MIT。

两年半MIT毕业，师从华裔教授赵宇飞

事实上，从2017年进入MIT学习，到2020年本科毕业、读上研一，Ashwin Sah也只用了两年半的时间。

自2018年1月以来，到今年11月，算上预印本，Ashwin Sah一共发表了 27篇论文。

他的本科论文已经有引用量，最高的一篇有8人引用，这篇是关于不规则图中独立集的数目的。

其他两篇引用较高的文章，虽然人数不多，但他也都是一作。

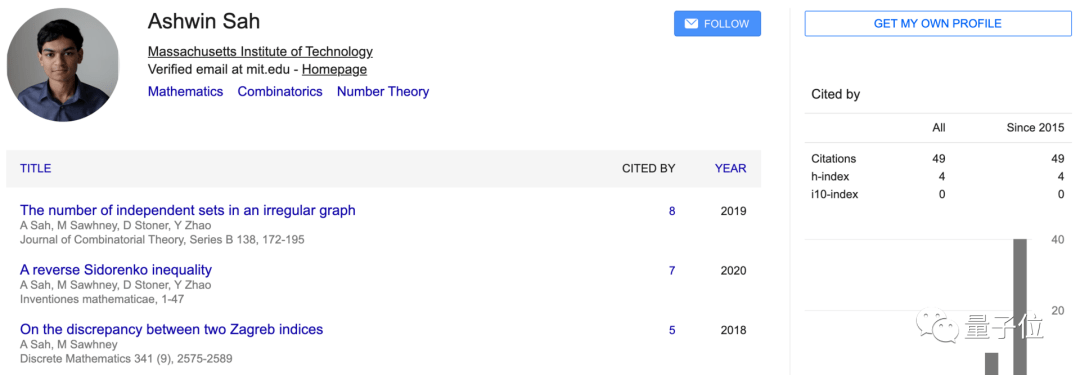
即使部分还是预印本，但本科期间就能获得这么多的研究成果，的确不得不令人赞叹。

除了自身的天赋与努力外，还有2位 「伯乐」般的人物，对他的数学发展起到了至关重要的作用。

首先是他的导师，MIT华裔知名数学教授 赵宇飞。

在MIT的第一年，Ashwin Sah修了一门课程，是与组合数学相关的研讨会。

但要知道，这门课程难度是研究生水平，而且汇集了全世界顶尖数学人才。

但即便如此，Ashwin Sah也在此脱颖而出。

作为这门课程的老师，赵宇飞这样评价道：

尽管他只是大一的学生，但很显然，他已经掌握了这门课程。

尽管他只是大一的学生，但很显然，他已经掌握了这门课程。

第二位重要人物，是比Ashwin Sah高一年级的学长， Mehtaab Sawhney。

Mehtaab Sawhney是在课堂上与Ashwin Sah相识，很快便成为了朋友。

这期间，他们共同进行了许多研究，主要与离散数学相关，包括其中的图论、概率和随机矩阵等。

但当时他们的所学知识还是有一定的局限，所以解决的问题普遍都比较简单，是不需要多年经验积累的那种。

正如Mehtaab Sawhney所说：

我喜欢解决的问题，是那种可以从基本原理开始思考，而不是那些需要翻阅大量的文献，或者拥有大量理论基础才能思考的问题。

我喜欢解决的问题，是那种可以从基本原理开始思考，而不是那些需要翻阅大量的文献，或者拥有大量理论基础才能思考的问题。

赵宇飞教授也会对他们进行指导，例如教他们如何写正式的论文。

他还会「派」给他们一些特定的问题，让他们去做研究，本以为会让他俩忙活一段时间。

但令赵宇飞万万没有想到的是……往往第二天，他们就把答案给交上来了。

就是如此的动力和效率，让他们在短短三年的时间里，能够完成几十篇论文。

赵宇飞对他们的评价非常之高，认为是他们所取得的成就是 史无前例：

（MIT）的本科生研究有着悠久的历史和传统，但在论文的质量和数量上，都达不到Ashwin Sah和Mehtaab Sawhney的水平。

（MIT）的本科生研究有着悠久的历史和传统，但在论文的质量和数量上，都达不到Ashwin Sah和Mehtaab Sawhney的水平。

目前，这两位小伙伴已经步入研究生生涯，他们还是保持着高频率的「会面」，用Sawhney的话就是：

我们每天见面一两次，每次五六个小时。

我们每天见面一两次，每次五六个小时。

即便存在疫情等客观原因，他们还是会保持非常高频率的信息互动。

「羡慕有研究方向高度重合的伙伴」

对于学生的报道，MIT助理教授赵宇飞第一时间进行了转发，表示祝贺。

网友们也第一时间送上了自己的祝福，并表示这样的故事非常激励自己，“就像一盆冷水泼到我的脸上，提醒我继续不断努力。”

也有人单纯对这份研究进展感到惊喜，并引用了Paul Erdos有关拉姆齐数的表述：

如果外星人要入侵地球，除非我们能给出R（5,5）的答案，那我们就算是有最聪明的人和计算机，也得用一年时间；要是外星人要R（6,6）的答案的话，那别想了，我们主动进攻吧。

如果外星人要入侵地球，除非我们能给出R（5,5）的答案，那我们就算是有最聪明的人和计算机，也得用一年时间；要是外星人要R（6,6）的答案的话，那别想了，我们主动进攻吧。

当然，对于他的研究经历，更多的是表示羡慕的网友：找一个研究方向高度重合的伙伴，共同提升效率，可是件非常不容易的事情。

那么，对于Ashwin Sah的经历，你有什么感想？

欢迎在评论区留言~

论文地址：

https://arxiv.org/abs/2005.09251