刚刚提出了KAN的MIT物理学家Max Tegmark和北大校友刘子鸣，又有一项重磅研究问世了！团队发现，它们用AI发现了物理学中的新方程，从此，AI很可能被引入物理学研究领域，帮助人类物理学家做出全新的发现。

就在刚刚，MIT物理学家用AI发现了物理学中的新方程。

论文地址：https://arxiv.org/abs/2405.04484

作者表示：这篇论文并没有解决价值数百万美元的核聚变问题，而是在更简单的设置中，引入一个有前途的概念验证。

偏微分方程（PDE），可以说是物理学家的面包和黄油，但它们非常罕见，人类科学家很难只用纸笔就能发现。

为此，研究者们推出了一个名为OptPDE的AI系统。

使用这个AI，就可以发现新的、从未见过的可积偏微分方程！

具体来说，使用了5000个随机初始化的PDE系数值运行OptPDE后，研究者发现了4个可积偏微分方程，其中是一个是已知的，而另外三个是全新的方程。

利用这种首创的机器学习方法，MIT的科学家们为物理学提供了一种全新的研究模式。
从此，可以由人类向系统提供领域知识，AI产生希望的假设，然后再由人类进行解释和验证。

这就实现了整个物理学发现的闭环。

网友：AI将颠覆各个科学领域

对于这项研究，网友们纷纷表示震撼。

「太烧脑了！如果我正确理解了他们的意思，那这个AI实在是强大到可怕！能够按需生成模型库来模拟物理系统，是非常巧妙的技巧，让我们可以从AI驱动的解决中，节省大量计算。」

「即便只在这些层面上，我们拥有的AI也能为各种科学领域提供新的见解和想法，它们会变得更好！」

「我只是点开看看是不是Max Tegmark大牛的研究，果然如此。」

这位网友则给出了更为专业的解释——

从本质上讲，他们是对偏微分方程应用了奖励函数，因为偏微分方程具有较多的CQs，并且自然系统遵循定律（例如热力学）。

由于发现这些偏微分方程往往非常困难，因此这项工作很有意义，因为它提供了一条将加速计算的计算杠杆应用于任务的途径。

这为生成类似OEIS（整数序列在线百科全书）的资源提供了机会。这就允许来自任何领域的研究搜索这些数据库，看看以前是否已经解决了类似的问题，或者相关的序列或结构是否已经存在，而不需要从头开始。

快速「入门」

当PDE具有守恒量时，它们是可积的（例如，能量是质量弹簧的一个守恒量）。

因此，研究者将OptPDE设计为一个两部分的系统，它可以——

（1）计算任何PDE的守恒量（CQ）数量；

（2）找出使n_CQ最大化的偏微分方程。

下面是（1）在一些熟悉的系统中的实际应用。

因为研究者寻找n_CQ的方法是可微分的，因此要发现新的可积偏微分方程，只需使PDE中的项系数可训练，并通过SGD最大化n_CQ即可。

他们以从u_x => u_xxx^3的项为基础，运行了5000次。

下面是解决方案的3D PCA——

研究者发现，他们得到大多数解，都是4个偏微分方程家族的线性组合，其中一个是KdV方程的一种形式，还有3个方程完全是新增的，在文献中并没有记载！

由此，研究者确认，这些新出现的可积偏微分方程中，至少具有一个守恒量。

也就是，在AI的帮助下，人类科学家发现了一些全新的可积偏微分方程！

不过，如果想解释和分析这些发现，还是要靠人类科学家。

研究者仔细分析了以下红色偏微分方程的简化版本（u_t=u_x^3），发现它表现出断裂、无限的CQ，而幂律衰减为了三角波。

从此，物理学家非常有希望使用OptPDE，来发现更多新颖的可积偏微分方程，来模拟物理学中的复杂现象。

不过，OptPDE要求AI和人类科学家协同工作，作者呼吁：如果这种范式能被物理学界接受，物理学家很可能用现代AI工具做出以前更多新发现。

可积系统：极其罕见，难以发现

可积系统在物理学和工程系中发挥着重要作用，因为易于处理、可预测、可控。

然而，它们极其罕见，难以发现。

传统中发现可积系统的方法是靠纸笔，它侧重于符号推到，还需要考虑到可能系统和守恒量（CQ）的指数级大搜索空间，效率极低。

由此，MIT的物理学家想到：AI可以做什么吗？

为此，他们引入了一个可积系统发现解决方案OptPDE。

此前，已经有许多工作使用极其学习从物理数据和微分方程中发现守恒量，但MIT研究者的方法，对于偏微分方程来说是最可解释的。

更重要的是，此前的方法并不能主动优化和设计偏微分方程。

然而，这个AI可以做到！

虽然过去机器学习方法已经被用来发现守恒量，但这项工作第一次提出——

通过验证和解释可集成系统，AI和人类科学家可以协同工作。

论文方法

研究者是通过以下阶段构建这个方法的。

1.CQFinder——查找PDE的守恒量。

2.OptPDE——使用CQFinder中的图片，来发现可积PDE。

图1说明了整个流程。不过需要注意的是，这个流程需要人类科学家通过输入CQ和PDE基础，和AI协同工作，这就需要对该领域知识的掌握。

OptPDE的可视化管线。给定PDE的项基础，OptPDE就会优化系数，从而最大化PDE的守恒量（CQ）数量。起初，u会衰减并且不守恒，但OptPDE会通过将扩散项归零，来发现使u更加守恒的系数。这个可视化示例很简单，但鉴于广泛的PDE基础，OptPDE可以帮助人类科学家发现新颖的可积系统

为了构建OptPDE，必须首先设计CQFinder，来准确计算任何PDE的CQ。

论文结果

CQFinder基准测试

为了验证CQFinder是否如大家设想的那样可以工作，研究者在Burgers、Korteweg-DeVries（Kd）和薛定谔方程三个测试系统上运行了它。

图2显示，奇异值曲线显示出从小到大的急剧相变，从而可以清楚地区分消失值和非消失值。

这就证明了，CQFinder不仅可以正确计算守恒量的数量，而且还可以获得它们的符号公式。

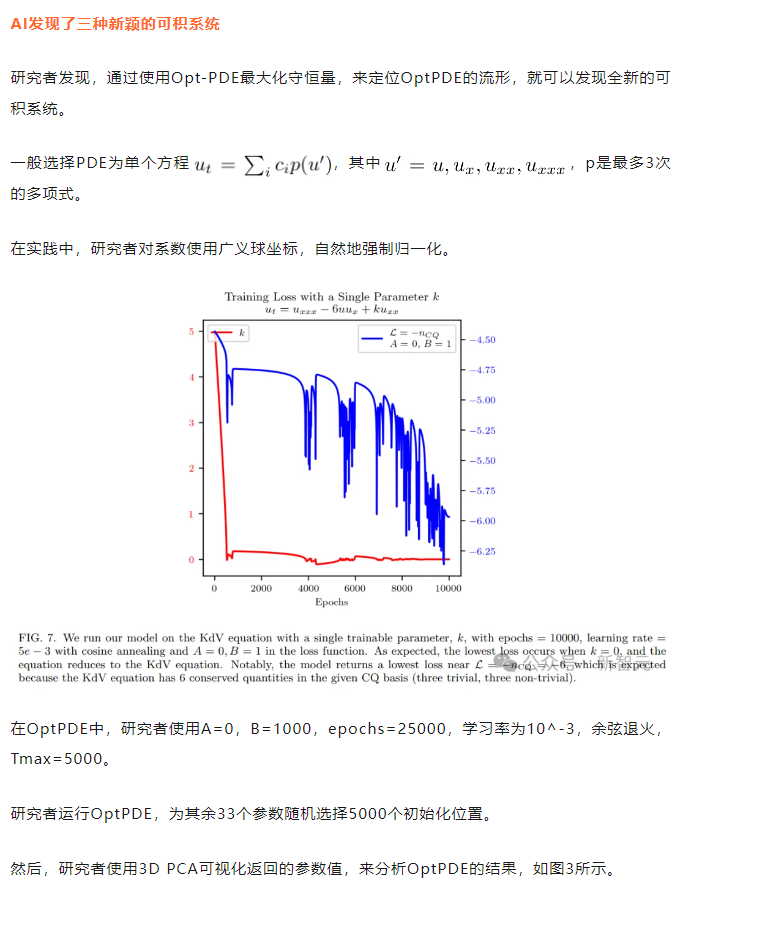
在Mathematica中，研究者绘制了具有高斯和正弦初始条件的偏微分方程的演化，如下图所示。

从视觉上看，演化似乎是一种波，在break time后就退化为了一种线性分量，此时，波在某一点就变得不可微分。

研究者推导了break time的符号形式，并为方程式在break time后的行为，创建了一个现象学模型。

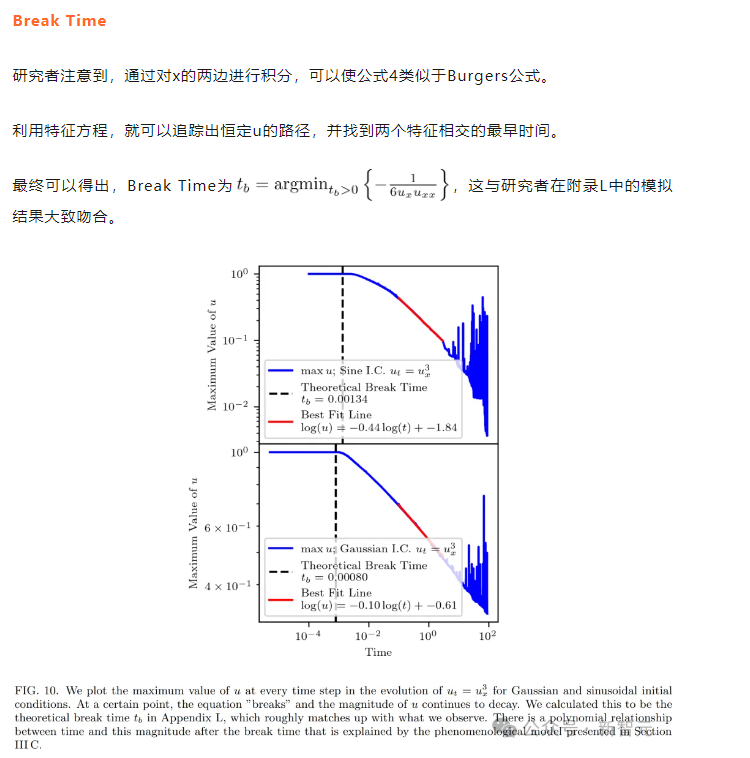
现象学模型

为了理解波break后的行为，研究者希望建立一个现象学模型，来解释波接近三角波时的动态。

对此，研究者进行了以下推导。

作者介绍

Subhash Kantamneni

Subhash Kantamneni目前在MIT攻读物理和计算机科学本科。

他在研究实验室、高科技创业公司以及对冲基金等多样化的工作环境中积累了丰富经验。

Ziming Liu（刘子鸣）

Ziming Liu目前是MIT和IAIFI的三年级博士生，由Max Tegmark教授指导。

他的研究兴趣主要集中在AI与物理学（以及其他科学领域）的交叉区域：

1. Physics of AI：从物理学原理来理解AI，目标是让「AI像物理学一样简单」；

2. Physics for AI：受物理学启发的AI，目标是让「AI像物理学一样自然」；

3. AI for physics：利用AI增强物理学研究，目标是让「让AI像物理学家一样强大」。

为了实现利用AI和物理学共建更美好世界的最终目标，Ziming Liu对包括发现物理定律、受物理启发的生成模型、机器学习理论、机械解释性等在内的多个主题都有深厚的兴趣。

并且，与凝聚态、高能物理、量子计算等领域的物理学家以及计算机科学家、生物学家、神经科学家和气候科学家等建立了紧密合作关系。

他多次在顶尖的物理期刊和AI会议上发表论文，并担任IEEE、Physical Review、NeurIPS、ICLR等的审稿人。同时，还共同组织了NeurIPS 2021和ICML 2022的AI4Science workshop。

在攻读博士学位之前，他在北京大学获得了物理学学士学位，并曾在微软亚洲研究院实习。

Max Tegmark

Max Tegmark被大家亲切地称为「疯狂的麦克斯」（Mad Max）。

凭借着自己创新的思维和对冒险的热情，他的科研兴趣涵盖从精确宇宙学到探索现实的终极本质。

比如，结合理论与新的测量技术，精确限定宇宙学模型及其参数。在他作为物理学研究者的前25年里，这种研究方向使他主要关注宇宙学和量子信息学。

虽然他仍与HERA合作研究宇宙学，但目前他的主要研究方向是智能的物理学，即运用物理方法深入探索生物智能和AI。

作为麻省理工学院的物理学教授，他发表了超过两百篇技术论文，并多次在科学纪录片中出现。他在SDSS项目中关于星系聚类的研究，赢得了《科学》杂志「2003年度突破」的第一名。

在此之前，Tegmark于1989年在斯德哥尔摩经济学院获得了经济学学士学位，1990年在皇家理工学院获得物理学学士学位。

毕业后，他便前往加州大学伯克利分校继续深造，先后获得物理学硕士和博士学位。

在美国西海岸生活四年后，他回到了欧洲，出任马克斯·普朗克物理研究所的助理研究员。

1996年，他作为Hubble Fellow以及普林斯顿高级研究院的研究员，再次来到美国。

几年后，他获得宾夕法尼亚大学的助理教授职位，并于2003年获得终身教职。

2004年，他来到MIT并定居在查尔斯河畔的剑桥。

他与妻子Meia-Chita Tegmark育有两个儿子，Philip和Alexander。

参考资料：
https://arxiv.org/abs/2405.04484
https://kindxiaoming.github.io/