度规,联络与测地线方程
爱因斯坦1905年提出的狭义相对论把时空统一成一个整体叫作闵可夫斯基时空。该时空内线长(时空间隔)由如下二次型决定

其中λ是个非零的仿射参数,是与作用量s对应的拉格朗日量。依据作用量原理,广义相对论里自由粒子走的路径取该作用量泛函s的极值。但考虑到根号形式的拉格朗日量在数学上不容易处理,所以我们转而将其平方

这就是广义相对论里自由粒子的运动方程,叫作“测地线方程”。当然我们亦可对的显式表达式直接变分从而得出与上述完全相同的测地线方程,即

化简整理后得到了与之前用作用量原理相同形式的测地线方程

可以发现最终得到了与之前用作用量原理完全相同的联络表达式。所以这意味着作用量原理和平行移动这两种看似不同的方法和出发点最终给出了相互自洽的结论。所以通过这一节的内容我们了解到:一旦给定了流形上的度规,我们就可以利用上式提取出与该度规相适配的联络。在下一节中,我们将进一步探究联络在坐标变换下的变换规律以及由联络导出的黎曼曲率张量分量在坐标变换下的变换规则。我们将发现:与联络不同的是,黎曼曲率张量的各分量在坐标变换下具有非常良好的变换性质(广义协变性)。对黎曼曲率张量做恰当缩并(可看成是黎曼曲率张量的某种平均)后给出的里奇张量和里奇标量也将成为真正进入到爱因斯坦场方程的关键组件。
联络及黎曼曲率张量分量在坐标变换下的变换规则
黎曼曲率由沿两个不同方向 和 间协变导数的对易子定义

而这一自洽性要求将自动给出之前新引进的修正项里联络各分量在坐标变换下的变换规则

从上式可发现:由于上述方程右端第二项的存在,联络各分量并不服从张量的变换规则。所以这意味着联络本身并不是张量!或者说,联络这个对象本身是个依赖于坐标系选取的量。尽管如此,它依然是广义相对论里非常重要的东西,因为以它为基本组件构造出的新的定义在流形上的“导数”运算 ----- 协变导数此时在坐标变换下具有非常良好的变换性质,即满足张量分量的变换规则。为了验证此时的协变导数的确服从张量分量的变换规则,可将上述得出的联络分量的变换规则重新代入坐标变换下协变导数的定义式
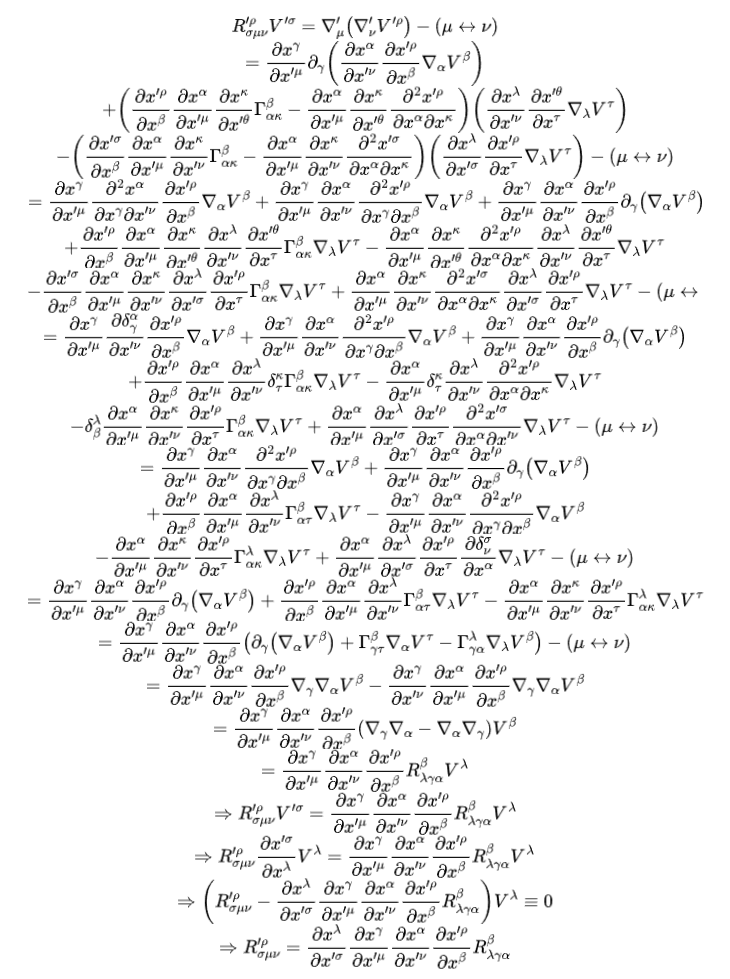
从上述推导中不难发现:黎曼曲率这个几何量是个张量,其分量服从正确的张量分量的变换规则。这也就证明了该曲率的内蕴性,即黎曼曲率这个对象本身是个与坐标选取无关的量。为了给之后的内容做铺垫,我们不妨在这里同时给出由黎曼曲率张量进行恰当缩并(可大致视为对黎曼曲率张量做的某种平均)后得到的里奇张量和里奇标量在坐标变换下的变换规律。其中里奇张量是黎曼曲率张量缩并一次后的结果,其分量在坐标变换下的变换规律容易从上述黎曼曲率张量各分量在坐标变换下的变换规律直接导出


注意这里的Rμν并不是之前提到的里奇张量,而只是用来呈现黎曼曲率张量内在数学结构的一个象征性的记号而已。从上式中可以清晰地看出方程右手边的头两项是联络的线性表达式,基本上对应联络的旋度;而方程右手边最后一项是沿 和 两方向上联络的对易子,它是关于联络的非线性(二次)表达式。这种数学结构在现代微分几何及纤维丛理论中具有非常广泛的普适性!我们将在下面对规范理论的讨论中看到几乎完全类似的数学结构再次出现。

















