19世纪末20世纪初,科学界涌现出了一种让人着迷的几何形态,这些形态充满了细碎和复杂的细节,看似无穷无尽。
这些几何形态的研究,虽然还未被命名为“分形”,但已经引发了数学家们的极大兴趣。
直到1974年,数学家本华·曼德博才首次提出“分形”这一概念,但在此之前,诸多数学家早已对这些形态展开了深入研究。
没错,今天我们来了解一下分形维度的问题。
01 早期的分形探讨
在分形正式命名之前,数学家们已经开始探索这些充满无限细节的几何形状。
瑞典数学家海尔格·冯·科赫便是其中的佼佼者,他设计了一种称为“科赫雪花”的曲线。
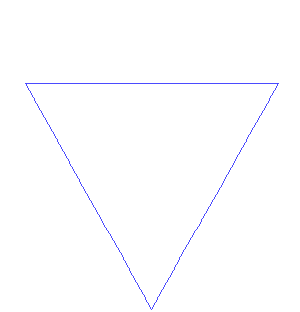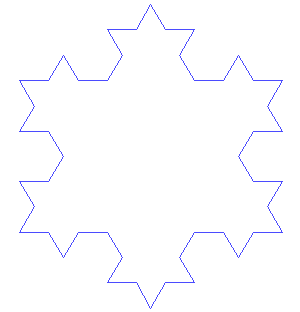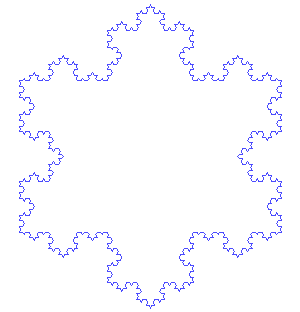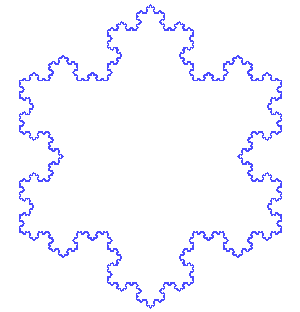
生成过程
它看似简单,但其背后蕴含了复杂的数学概念。
科赫的雪花形状无论放大多少次,依然呈现出相似的形态,且每一层次都蕴含着无限的细节。
与科赫雪花异曲同工的,还有德国数学家戴维·希尔伯特的曲线。
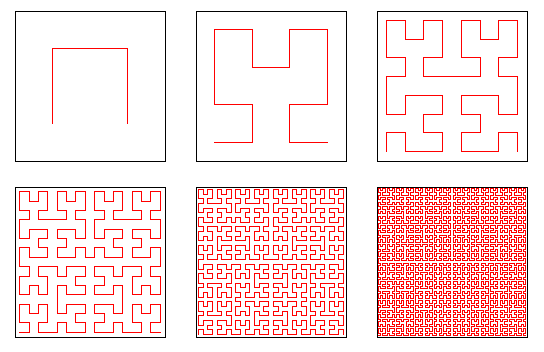
希尔伯特曲线
希尔伯特曲线与意大利数学家朱塞佩·佩亚诺的曲线非常相似,都是将一个线段通过复杂的方式弯曲成充满自相似性的形状。
而日本数学家高木贞治则提出了“牛奶冻曲线”,这些复杂而富有美感的曲线展示了数学世界中独特的美。
牛奶冻函数的图形
康托尔的贡献则是发明了“三分集”,这是一个看似简单的点集,但其复杂性却令数学家们难以捉摸。这一组点集难以被简单归类为一维或零维,使人们开始思考维度的本质。

不仅如此,奥地利数学家卡尔·门格还提出了“门格海绵”,一种看起来像体积,却又充满空洞的三维物体。
门格海绵的每一个切面都显示出无穷无尽的细节,使其在维度上的定义变得模糊不清。

门格海绵
02 谢尔宾斯基三角形的奥秘
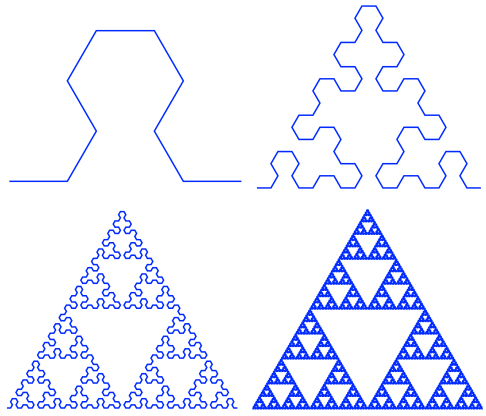
要说在这些复杂几何形态中谁的最引人注目,那当然是波兰数学家瓦茨瓦夫·谢尔宾斯基在1915年提出的三角形了。

谢尔宾斯基三角形
谢尔宾斯基三角形是一个等边三角形,其中充满了不断缩小的三角形,这些三角形相互嵌套,形成了一个无穷细碎的图形。
谢尔宾斯基三角形的独特之处在于,它可以通过两种不同的方式构造:
一种是通过增加边线的方式,
另一种是通过在面上挖空的方式。
这两条路径看似来自不同的维度,但最终却指向了同一个目标——构造出谢尔宾斯基三角形。这意味着,这个图形在维度上具有极大的模糊性。
在传统的几何学中,我们习惯于将形状归为一维、二维或三维,但谢尔宾斯基三角形打破了这种传统的分类方式。
它既不是一条线,也不是一个面,而是介于两者之间的“另类”存在。
为了探究谢尔宾斯基三角形的真实维度,我们需要借助对数表来计算。
这个结果显示,谢尔宾斯基三角形的维度并非整数,而是一个小数——1.585。
这一发现令人震惊,因为它意味着这个图形在维度上处于一维和二维之间。
03 分形维度的神秘世界
这种介于整数维度之间的小数维度为我们打开了通往全新几何世界的大门。
谢尔宾斯基三角形并非孤例,事实上,许多自然界的形状都展现出类似的分形特征。
山峦、河流、树木的形状,甚至人体内的血管网络,都具有分形的特性。
本华·曼德博在1982年出版的《大自然的分形几何学》一书中,详细阐述了分形的概念,并举例说明了其在自然界中的广泛存在。

达芬奇手稿
例如,花椰菜的表面复杂度可以用2.33维来描述,而西兰花则具有2.66维的复杂度。
人类的肺部,其表面与空气接触的复杂度接近于3维,几乎已经成为一个“容积”。
尽管分形在数学家们的抽屉中躺了几十年,看似只是一种理论上的奇珍异宝,但本华·曼德博的研究彻底改变了这一状况。他意识到,分形理论不仅仅是一种数学上的趣味,而是可以应用于实际问题的强大工具。
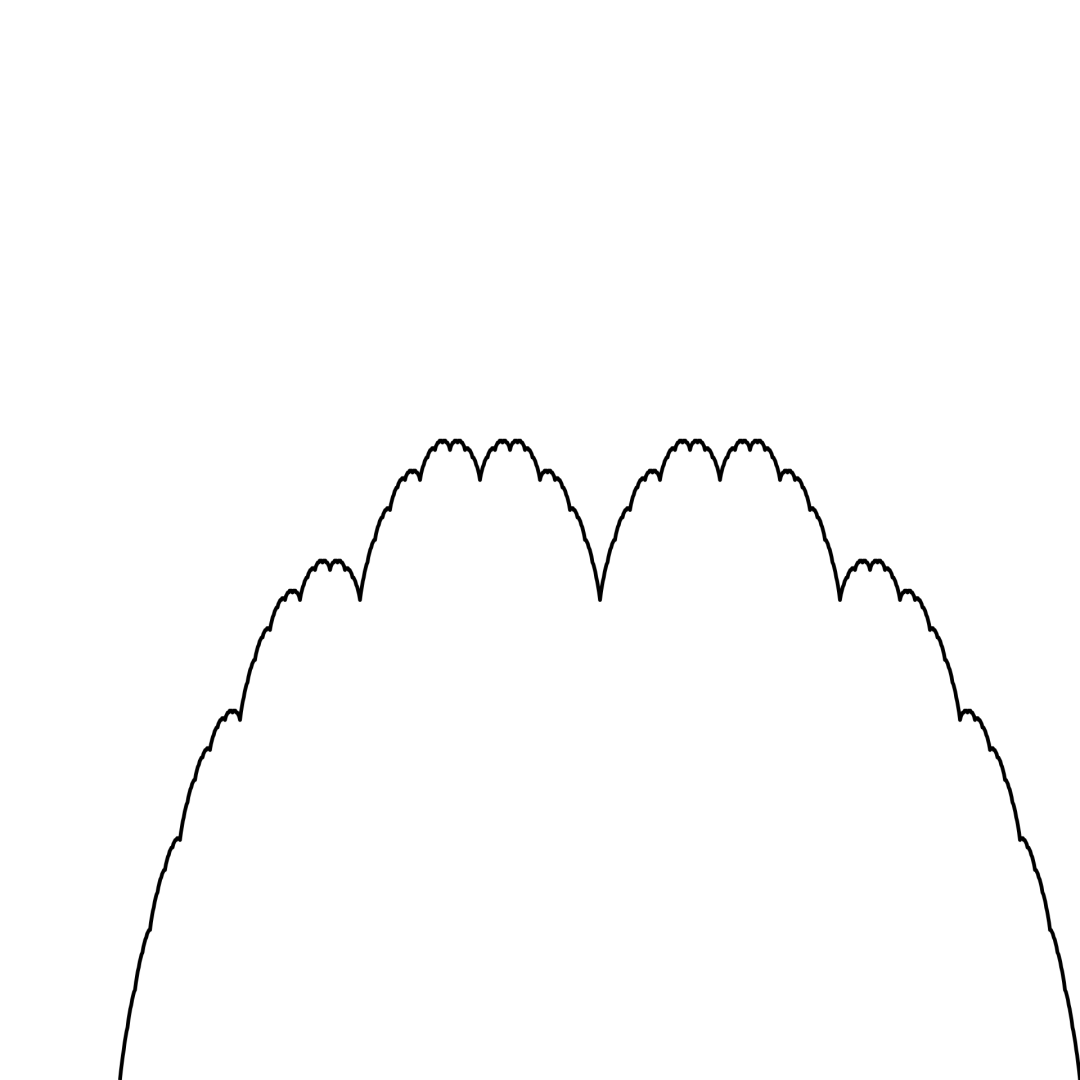
曼德博通过对英国海岸线的研究,证明了分形维度可以用来测量复杂的自然边界。

分的越细,海岸线越长
他计算出英国海岸线的维度为1.25维,这表明这条海岸线的复杂度介于一条直线与一个平面之间。类似地,西班牙与葡萄牙之间的国界线也展现出类似的分形特征。
分形维度的测量方法虽然听起来抽象,但它提供了一个更为精确的方式来描述那些难以用传统几何学测量的形状。随着时间的推移,分形的应用范围不断扩大,从自然科学到工程学,甚至艺术领域,分形都展现出了其独特的魅力。
分形研究的最大惊喜或许在于,直到20世纪,科学才开始真正关注这些在我们世界中无处不在的形状。
分形就像是一种被忽视的宝藏,长久以来一直存在于我们的眼前,但直到最近才被科学家们揭示出来。
回顾分形的发展历程,我们不禁要问:
在我们身边,还有多少未被发现的“分形”?
这个世界上还有什么未被了解的奥秘,只因我们从未想到要去探索?
或许,有时候答案就藏在我们看似平凡的周围,只等待我们抬起头、睁大眼睛,去发现它们。
总结
3维空间中,也会有4维的东西!这就是分形。
分形的世界是一个充满未知和惊喜的领域,它不仅挑战了我们对维度的传统认知,也让我们重新思考自然界的无穷复杂性。
随着科学的不断进步,分形将继续引领我们走向新的发现,揭示出这个世界的更多奥秘。

















