
「封面」|100以内的质数
质数是指除了1和它本身以外,没有其他数可以整除的数字。
我们刚开始接触“质数”这个概念是在小学的时候,当时教科书要求我们熟记100以内的所有质数。听说现在的小学数学教材,已经开始教学生如何用一种叫“质数筛”的方法来判断100以内的数字是否为质数。
但是,问题在于,我们当时学习的时候并没有对质数了解那么深,甚至也没有心思去思考质数背后的数学原理。
这,真的很可惜!
为了研究质数,其实你不知道“孕育”了多少杰出的数学家,甚至因为质数本身还可以享受荣华富贵。
好,本篇我们就来讲一个人的故事。
01
1991年,张益唐,这位后来在数学界掀起波澜的美籍华人,在美国普渡大学顺利完成了他的数学博士学位。
然而,命运似乎并没有为他准备好一条顺畅的道路。
毕业后的他,遇到了求职的艰难局面,甚至一度落魄到住在车里谋生。
为了维持生计,他曾在快餐店打工,也在汽车旅馆里做过清洁工。
但无论生活如何困苦,数学一直是他心灵的庇护所。许多年来,他固执地钻研一个闻名遐迩却未曾解决的数学难题——孪生质数猜想。
孪生质数,听起来颇具浪漫色彩。它指的是这样一对质数:它们之间的差值恰好为2。例如,3和5是一对孪生质数,因为两者都是质数,且5-3=2。
同样,11和13也是孪生质数,13-11=2。
在更大的数域中,还有类似16829和16831这样的孪生质数。
这个问题引发了数学家的无限遐思——在无穷的数轴上,是否存在无穷多对这样的孪生质数?
这个简单却深奥的猜想,数百年来吸引着无数数学家。
张益唐并非为了追求名利而研究这个猜想。
他的初衷仅仅是想揭开数学世界中的这一神秘面纱。就这样,他在寂寞的数学世界里坚守着,不为外界的喧嚣所动,专注于自己的研究。
2013年,张益唐在新罕布什尔大学担任临时讲师,这份临时教职并不足以让他名扬四海。
然而,就是在这一年,他将自己辛苦研究的成果整理成了一篇论文,并寄给了《数学年刊》——数学界最负盛名的期刊之一。
编辑们打开这篇论文时,眼前的文字简直让他们难以置信。
张益唐竟然解决了孪生质数猜想吗?
严格来说,张益唐并未完全证明这个猜想,但他的工作在数学界引起了极大的轰动。他证明了存在无穷多对质数,它们之间的差值不到7000万。
虽然与孪生质数之间仅差2的结果相比,这个差值似乎庞大得不可思议,但对于数学家们而言,这已经是一个里程碑式的突破。
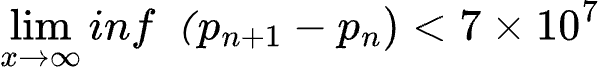
或许你会觉得,相差7000万的质数对并没有那么令人兴奋,但在数学家的眼中,这个突破意味着距离解决孪生质数猜想更近了一步。
更令人惊叹的是,这项发现来自于一位在数学界默默无闻的研究者,这让整个事件更加戏剧化。

张益唐
张益唐也因此获得了“麦克阿瑟奖”,这一奖项又被称为“天才奖”,是对他卓越贡献的肯定。
随后,他辞去了临时讲师的职位,前往普林斯顿大学开始了新的职业生涯。
质数自古以来就充满了神秘色彩,人们常常赋予它们以人性化的特质,仿佛这些数字也有着自己的喜好和行为模式。
质数之间似乎喜欢聚集在一起,尤其是在数轴的前端,这种“群居”现象更为明显。
例如,在前10个自然数中,质数的比例达到40%;
在前100个自然数中,这一比例下降到25%;
而在前1000个自然数中,比例则进一步下降到16.8%。
尽管我们知道质数是无穷多的,但它们之间的分布却随着数轴延展而变得稀疏。
除了2和3这一对相差1的特殊质数外,其他的质数对之间至少相差2。
然而,数学家们一直坚信,质数之间存在某种趋近于“亲密”的关系,特别是孪生质数这一概念,让他们坚定地相信,在无穷数轴上,必定有无穷多对相差2的质数。
数学家们甚至为那些相差不大但差距超过2的质数对起了名字。
例如,两个相差4的质数被称为“表兄弟质数”,像7和11,19和23就是典型的表兄弟质数。而相差6的质数则被称为“六质数”(sexy prime),这一名称来源于拉丁语中“六”的发音,例如5和11就是一对六质数。
然而,这些质数对之间的关系仍然无法与孪生质数相比拟,孪生质数在数学家心中的地位几乎是无可替代的。
那么,为什么张益唐的发现如此重要呢?
虽然7000万的差值与孪生质数的差值2相比,显得遥远无比,但至少张益唐证明了存在无穷多对相差有限数值的质数。
这一突破大大增强了数学家们最终证明孪生质数猜想的信心。

张益唐的工作证明了,即使在数轴的远端,质数的分布虽然稀疏,但其中依然有无穷多个质数对,彼此差距在有限的范围内。
自从张益唐的成果发布以来,数学界的研究者们开始协力合作,试图进一步缩小他所提出的质数对之间的差值。
如今,研究已经取得了新的进展,科学家们已经证明存在无穷多对相差不超过几百的质数。
如果有一天,这个差值能够缩小到2,那么孪生质数猜想就可以成为定理。
总结:
张益唐的故事不仅是一个数学问题的突破,更是一个关于坚持与信仰的传奇。他让我们看到了,在科学的世界里,真正的英雄往往默默无闻,但他们的发现却能撼动整个世界。

















