量子纠缠，作为量子力学的核心现象之一，其神秘性和非直观性一直以来都吸引着物理学家的极大关注。在经典物理学中，粒子之间的相互作用是局限于它们之间的距离和相对运动的，但在量子力学中，两个纠缠粒子即使被分隔在遥远的距离下，依然能瞬间影响彼此的状态。这种现象引发了“量子非定域性”的讨论，挑战了传统的时空观念。

而当我们将这些量子纠缠的粒子置于相对论效应显著的环境中，比如一个在高速飞行的飞船和地球之间分隔的纠缠粒子，我们会面临更复杂的科学问题。高速飞船上的粒子将受到相对论效应的影响，例如时间膨胀和长度收缩，这可能会对量子纠缠的同步性产生影响。在这种情况下，纠缠粒子的同步性是否能够保持？相对论效应会如何改变量子纠缠的性质？这些问题不仅涉及量子力学的基础，也牵涉到现代物理学中的核心理论——相对论和量子力学的统一性。让我们深入探讨这些问题，揭示量子纠缠在相对论效应下的奥秘。

1. 量子纠缠的基本概念

量子纠缠是量子力学中一种非经典的现象，当两个粒子处于纠缠态时，它们的量子状态相互依赖，即使它们被分隔在很远的距离，改变一个粒子的状态会瞬间影响到另一个粒子。这种现象被爱因斯坦形容为“鬼魅般的远距离作用”，它挑战了经典物理学中的局部性概念。

1.1 量子纠缠的实验验证

量子纠缠的实验验证可以追溯到20世纪初。最著名的实验包括阿斯佩实验（Aspect experiment），它验证了爱因斯坦-波多尔斯基-罗森悖论（EPR悖论）中的纠缠特性。阿斯佩实验通过测量纠缠光子的极化状态，证明了量子纠缠的非局域性，进一步巩固了量子力学的预测。

1.2 纠缠态的数学描述

量子纠缠态通常通过波函数来描述。例如，贝尔态是描述两个纠缠粒子的经典例子。贝尔态可以写作：

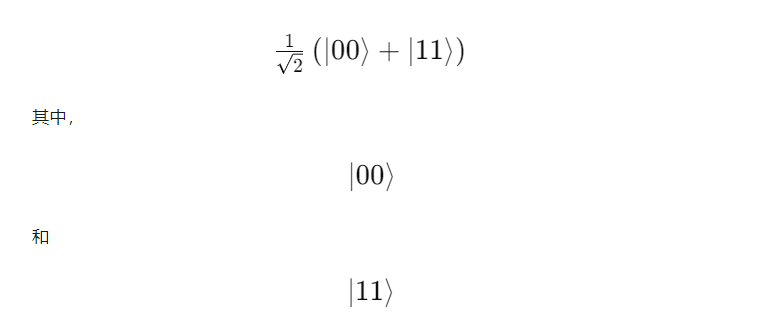
分别表示两个粒子的状态。纠缠态的特性在于无论如何对一个粒子进行测量，另一个粒子的状态都将立即被确定。

2. 相对论效应的基本概念

狭义相对论由爱因斯坦于1905年提出，它主要涉及高速运动下的时间和空间的变化。主要效应包括时间膨胀和长度收缩。

2.1 时间膨胀

时间膨胀是指在一个快速移动的参考系中，时间流逝的速度会比在静止参考系中慢。公式为：

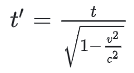
其中，t′是快速参考系中的时间，t 是静止参考系中的时间，v是相对速度，c是光速。

2.2 长度收缩

长度收缩指的是在高速运动的参考系中，物体的长度会沿运动方向缩短。公式为：

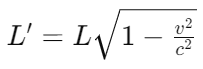
其中，L′是高速参考系中的长度，L是静止参考系中的长度。

3. 量子纠缠与相对论的结合

量子纠缠和相对论的结合是现代物理学中的一个重要问题。我们需要探讨在不同的参考系下，纠缠粒子的同步性是否仍然保持不变。

3.1 参考系转换中的同步性问题

在相对论效应下，如何定义和测量粒子的状态变得复杂。例如，假设一个纠缠对的粒子分别位于地球和一个快速飞船上。根据狭义相对论，飞船上的粒子经历的时间比地球上的粒子要慢。如果我们在飞船上测量一个粒子，地球上的粒子是否会立即同步改变其状态？

3.2 实验中的观察与解释

实验上，我们可以利用纠缠光子对来测试这种情况。例如，如果一个光子从地球发送到飞船，另一个光子则留在地球，测量飞船上的光子是否会影响到地球上的光子。这种实验可能会受到相对论效应的影响，比如时间膨胀和信号传输延迟。

4. 相对论对量子纠缠的影响

虽然量子纠缠的非局域性在经典意义上是瞬时的，但相对论效应可能会对其表现出不同的特性。

4.1 量子信息的传输

在量子信息的传输中，尽管纠缠粒子间的状态是瞬时变化的，但实际的信息传输速度仍受光速限制。因此，量子纠缠不能用来超越光速进行信息传递，这符合相对论的要求。

4.2 相对论性量子力学的模型

相对论性量子力学（如狄拉克方程）试图将量子力学和相对论统一起来。在这种理论框架下，纠缠态的描述也需要考虑相对论效应，例如，利用洛伦兹变换来理解粒子的状态如何在不同的参考系下表现。

5. 实验验证与挑战

在实际的实验中，验证纠缠粒子在相对论效应下的同步性面临许多挑战。主要挑战包括：

5.1 高速飞行实验的困难

要在高速飞行的飞船上进行实验，需要在极端条件下维持粒子的纠缠状态。当前技术水平限制了这种实验的实施，尤其是在长时间和高速度的情况下。

5.2 数据解析与理论模型

将实验数据与理论模型进行比对需要精确的计算和分析。相对论效应的复杂性使得这种比对变得更加困难，特别是在高精度实验中。

6. 结论与展望

尽管目前我们无法完全实现高速飞行的实验，但量子纠缠和相对论效应的结合仍然是一个值得深入研究的领域。通过进一步的理论研究和实验探索，我们有望更好地理解量子纠缠在不同参考系下的表现，并推进量子力学与相对论的统一。