吾曰:还想把麦克斯韦方程组研究透彻一点。
师曰:那个只是波动方程,很简单。可继续伽罗瓦群论。上篇写得不错!还可继续深化,方程次数降低的过程,与伽罗瓦群寻找子群的过程,同构。
再次猛醒,此处紧要,而仍晦暗。于是再提笔,以期不辜负师之殷切教导。
我们从1元2次方程,渐次剖析到1元5次方程。
1元2次方程
X² + bX + c = 0
解方程的过程,本质上是方程次数降低的过程,示例如下。
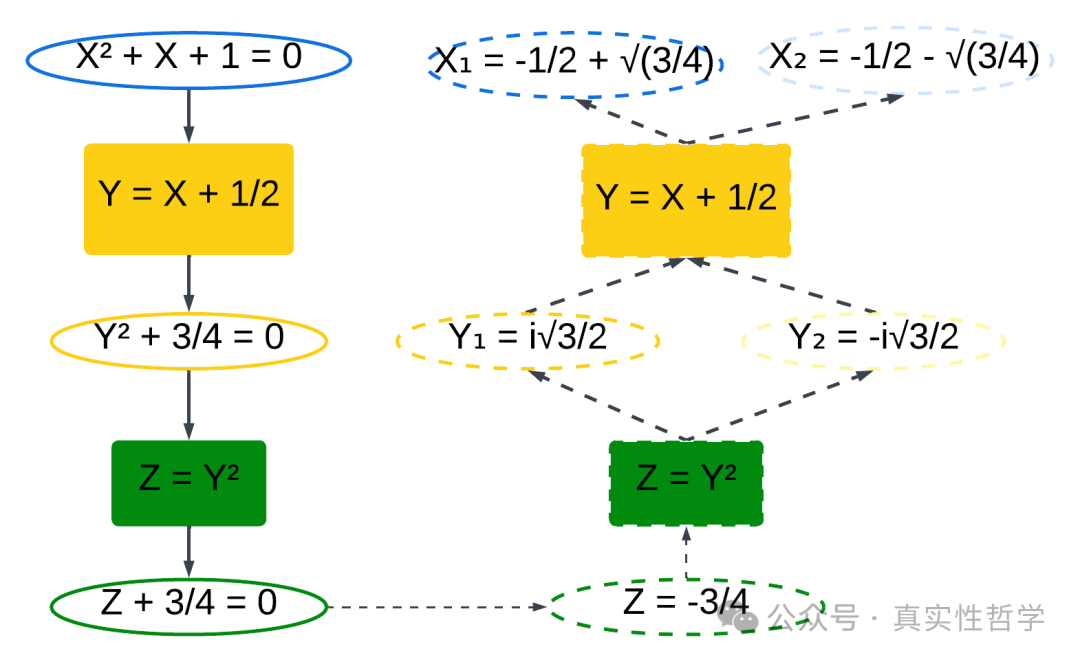
先看正向的方程变换过程。
正向第一步,根据同构映射关系Y = X + 1/2,X同构映射到Y,从X的1元2次方程X² + bX + c = 0变成了Y的1元2次方程Y² + 3/4 = 0,而且消去了1次项。
正向第二步,根据同态映射关系Z = Y²(对应根式扩展),Y同态映射到Z,从Y的1元2次方程Y² + 3/4 = 0变成Z的1元1次方程Z + 3/4 = 0。
再看反向的根式求解过程。
反向第一步,根据Z的线性方程,求得Z。
反向第二步,通过Z,由根式扩展Z = Y²得到成对出现的Y。
反向第三步,通过Y,由同构映射Y = X + 1/2得到对应的X。
伽罗瓦群与系数域和包含根式解的扩展域的关系如下。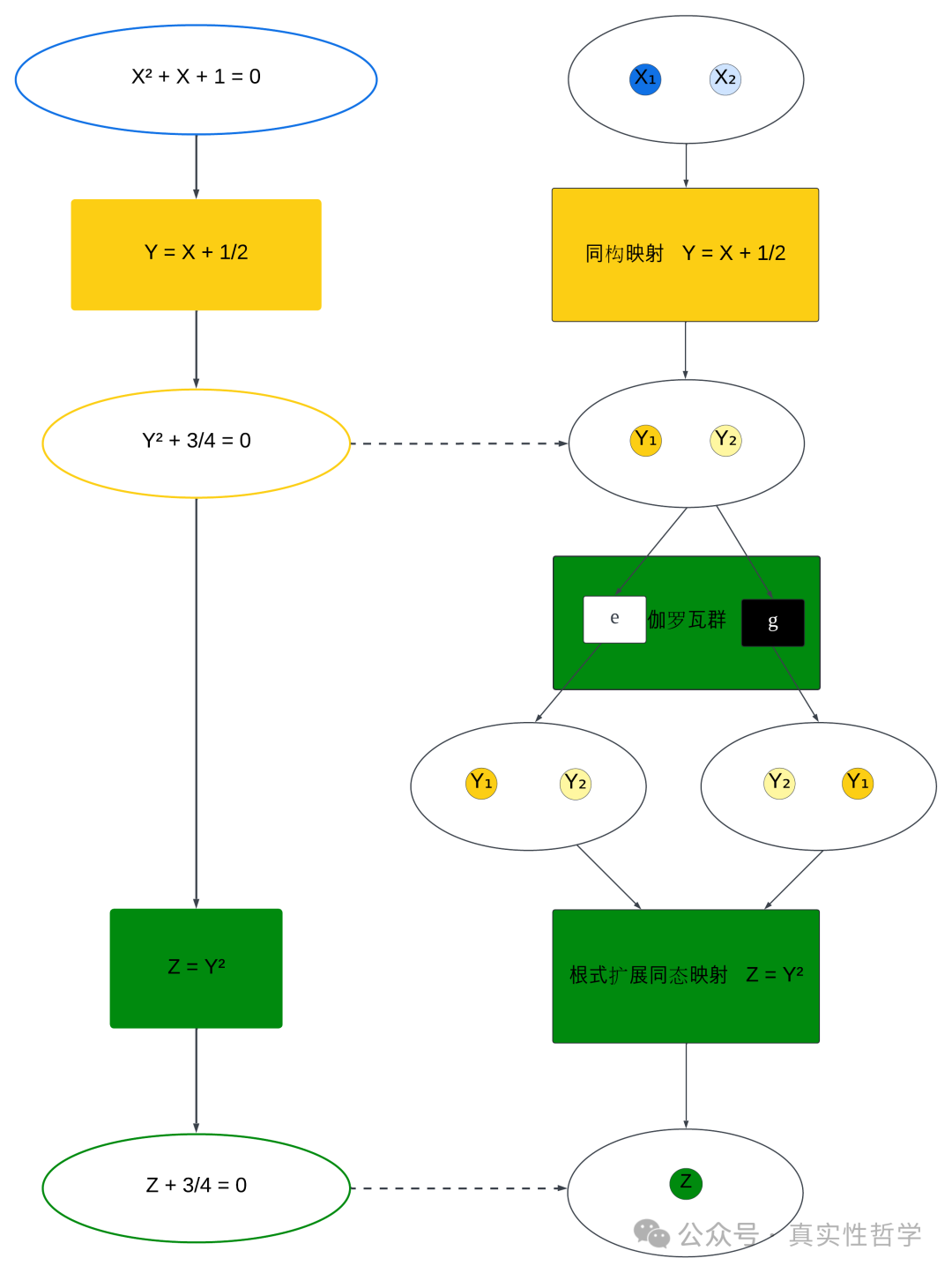
所谓伽罗瓦群,即保持系数域不动的扩展域的所有自同构映射组成的群。
1元方程从2次降到1次,对应2阶伽罗瓦群{e, g}找到子群1阶单位元群{e}。
1元3次方程
X³ + bX² + cX + d = 0
解方程的过程,本质上是方程次数降低的过程,示例如下。
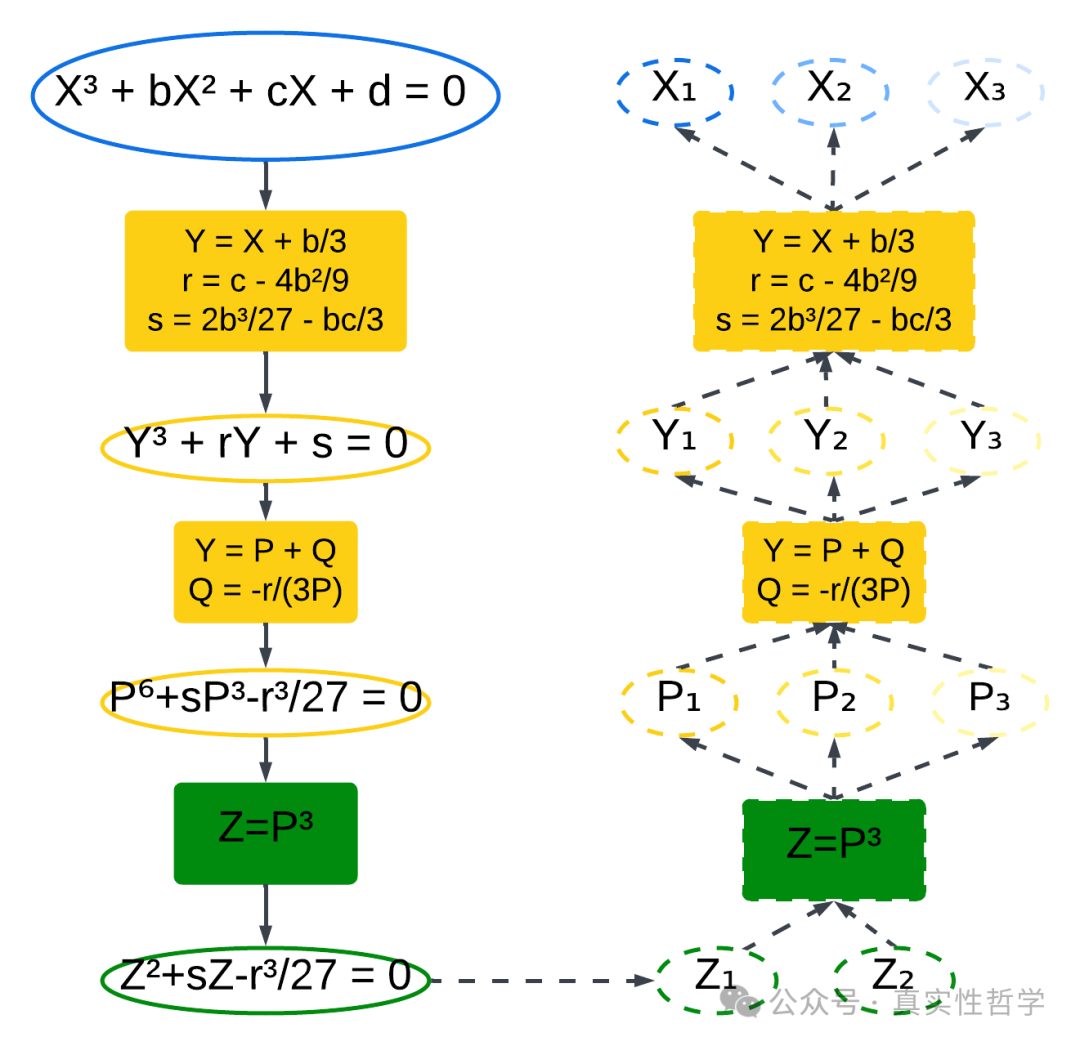
由上图可见,可将1元3次方程通过同构映射与3次幂同态映射转变为1元2次方程。
方程次数降低的过程,与伽罗瓦群寻找子群同构。

由上图可见,1元3次方程的根式解扩展域,在相对于1元2次方程所在域的伽罗瓦群(e, f, f²)的同构映射下,所有根式解在根式扩展同态映射Z=P³都会对应到相同Z,即所有伽罗瓦群内的同构映射都保持了Z点不动。
而Z属于变换后的1元2次方程的根式解的扩展域,在相对于1元1次方程所在域(即系数域)的伽罗瓦群(e, g)的同构映射下,可以保持1元1次方程的系数域不动。
1元4次方程
X⁴ + bX³ + cX² + dX + e = 0
解方程的过程,本质上是方程次数降低的过程,示例如下。
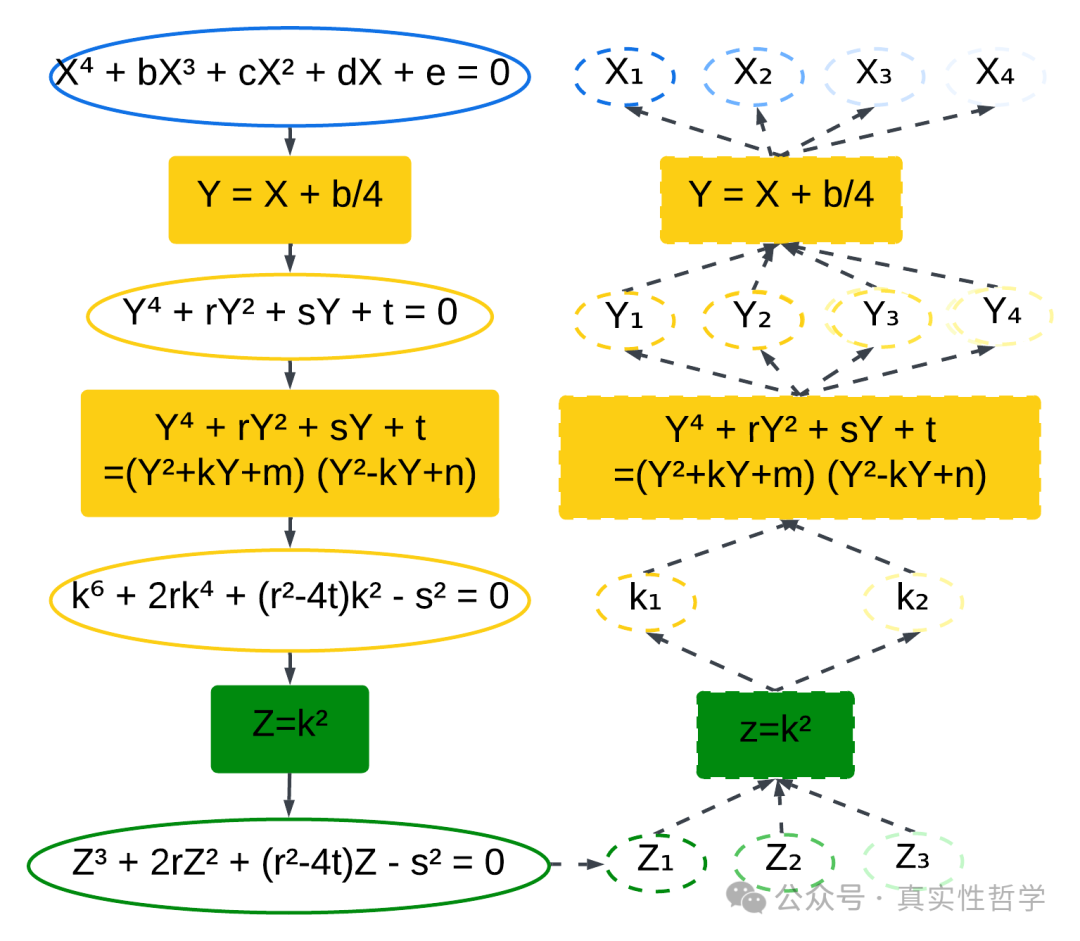
方程次数降低的过程,与伽罗瓦群寻找子群同构。
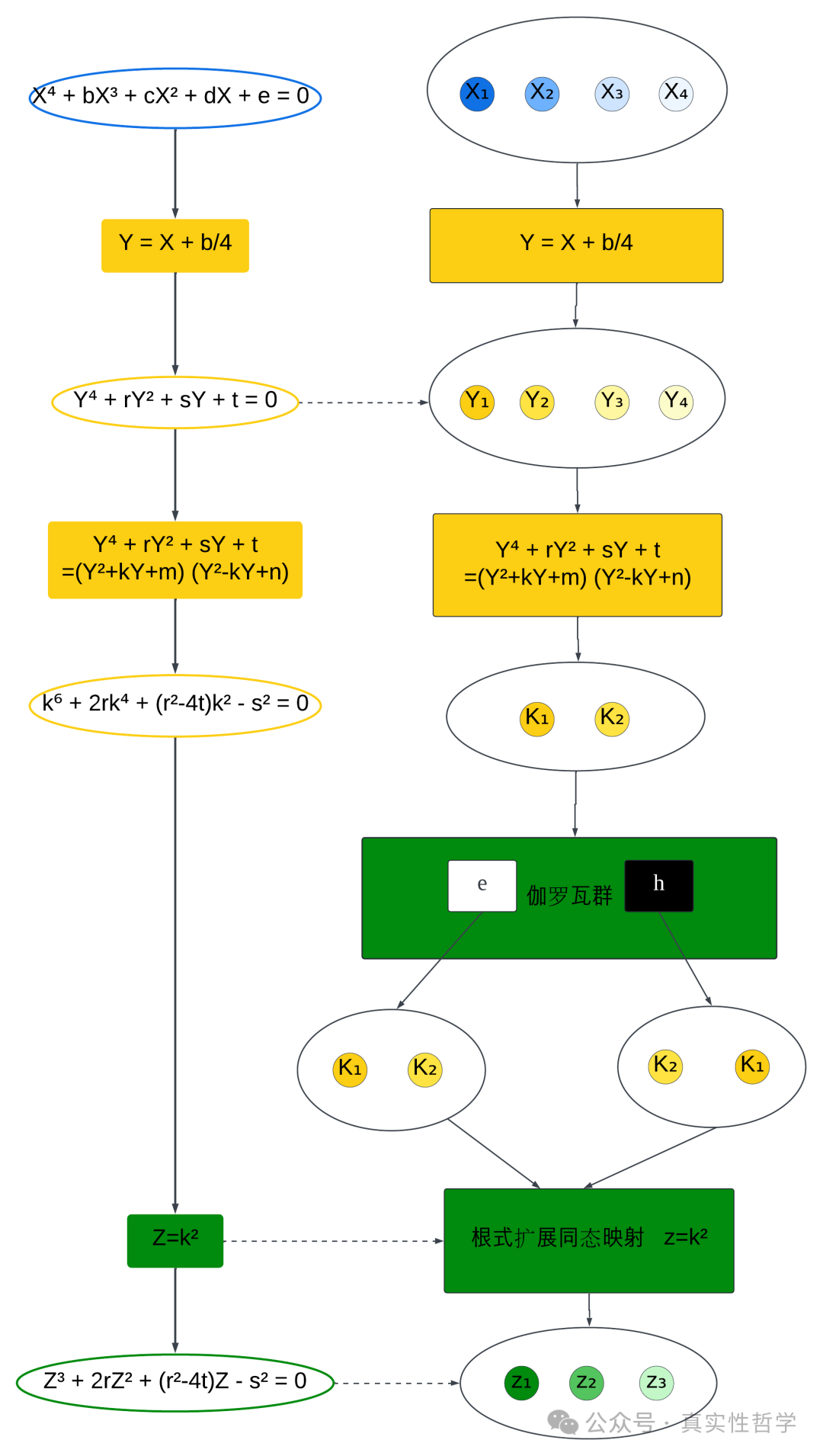
由上图可见,1元4次方程的根式解扩展域,在相对于1元3次方程所在域的伽罗瓦群(e, h)的同构映射下,所有根式解在根式扩展同态映射z=k²都会对应到相同z,即所有伽罗瓦群内的同构映射都保持了z点不动。
而z属于变换后的1元3次方程的根式解的扩展域,依次变换,可以变为1元2次方程,再变为1元1次方程。整合如下。
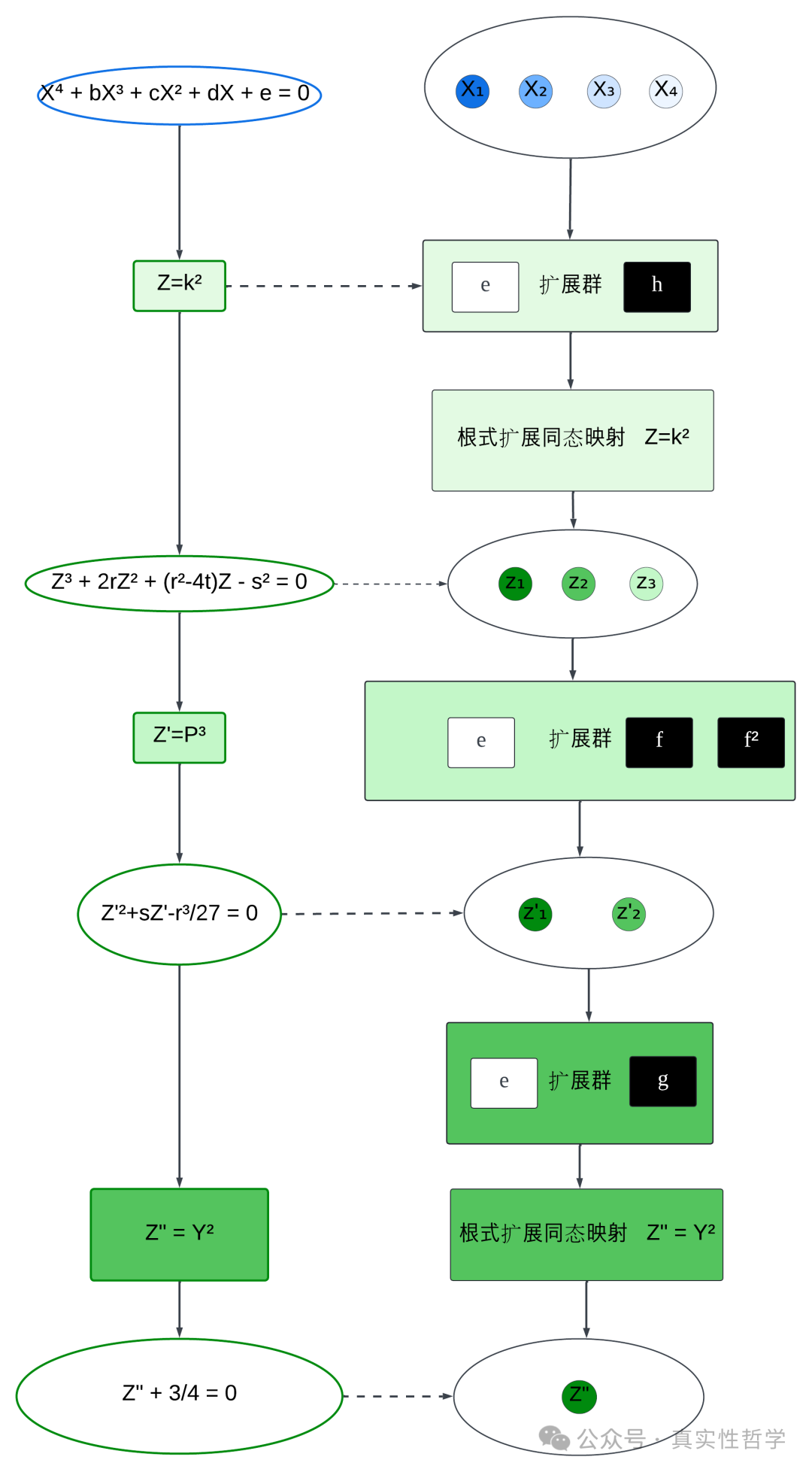
由上图可见,1元4次方程,可粗略地视为,由1元1次方程经过2次幂函数(Z"=Y²),再经过3次幂函数(Z'=P³),再经过2次幂函数(Z=k²)扩展而来,其中还经过了同构映射变换。
而对应的,可视为循环群的多次扩展,即先从单位元群{e}扩展出第1层扩展群{e, g}(第1层扩展域相对于系数域的伽罗瓦群), 再扩展出第2层扩展群{e, f, f²}(第2层扩展域相对于第1层扩展域的伽罗瓦群),再扩展出第3层扩展群{e, h}(第3层扩展域相对于第2层扩展域的伽罗瓦群)。
而,最外层即第3层扩展域相对于系数域的扩展群(即1元4次方程根所在的域相对于系数域的伽罗瓦群)可视为1、2、3层扩展群的乘积{e, g} * {e, f, f²} * {e, h}, 第2层扩展域相对于系数域的扩展群可视为1、2层扩展群的乘积{e, g} * {e, f, f²},第1层扩展域相对于系数域的扩展群即为{e, g} ,而系数域保持自身不动的同构映射为恒等映射单位元群{e}。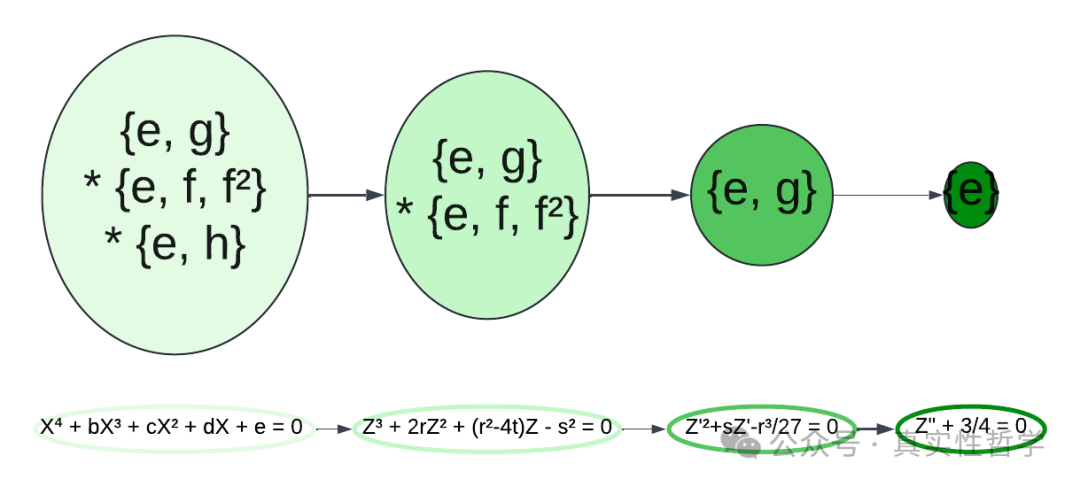
由上可见,方程次数降低的过程,与伽罗瓦群寻找子群的过程,同构。
1元5次方程
X⁵ + bX⁴ + cX³ + dX² + eX + f = 0
为什么1元5次方程没有通用的根式解?
以X⁵ - X - 1 = 0为例,它没有通用的根式解。
反证法。假设它有根式解,那么X⁵ - X - 1 = 0 可分解为(X - x₁)(X - x₂)(X - x₃)(X - x₄)(X - x₅)= 0, 那么x₁、x₂、x₃、x₄、x₅在系数域的基础上生成的扩展域的伽罗瓦群,可用循环群逐层扩展而来。
下面我们将证明这不可能。
包含所有3元循环置换的5阶群的子群,是扩展域的同构映射,并能保持系数域不动。那么,包含所有3元循环置换的5阶群的子群,能否由恒等映射单位元群通过循环群逐层扩展而来呢?不能!
我们在<伽罗瓦群论通俗导论 1 扩展的结构——1元5次方程为何没有通用的根式解?> 已经证明包含所有3元循环置换的群的交换子会出现在每一层的扩展群中,而包含所有3元循环置换的群不是可交换群,即没办法通过群的子群(以循环群为等价商群)逐渐缩小到恒等映射单位元群。
下图表明,伽罗瓦群可由循环群(根式扩展)组层扩展而来。
内层合并扩展群 = 总体合并伽罗瓦群 / 外层循环群
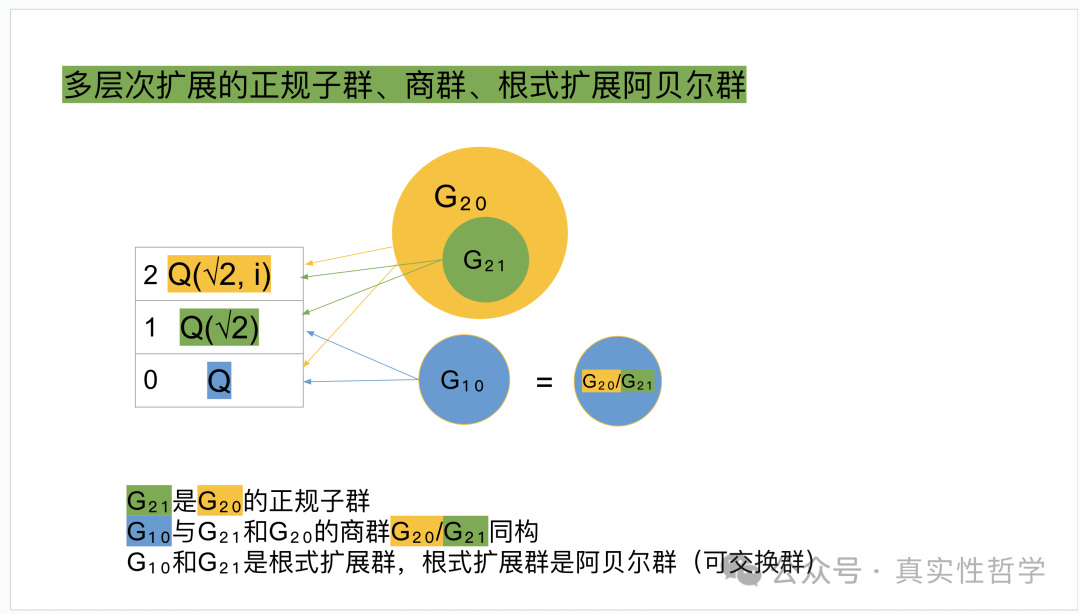
下图表明,包含所有3元循环置换的群的交换子也是3元循环置换,会一直出现在所有逐层向内的内层扩展群中,而包含所有3元循环置换的群不是可交换群、进而不是循环群,所以假设的伽罗瓦群无法由循环群逐层扩展而来,即存在1元5次方程无法用根式求解。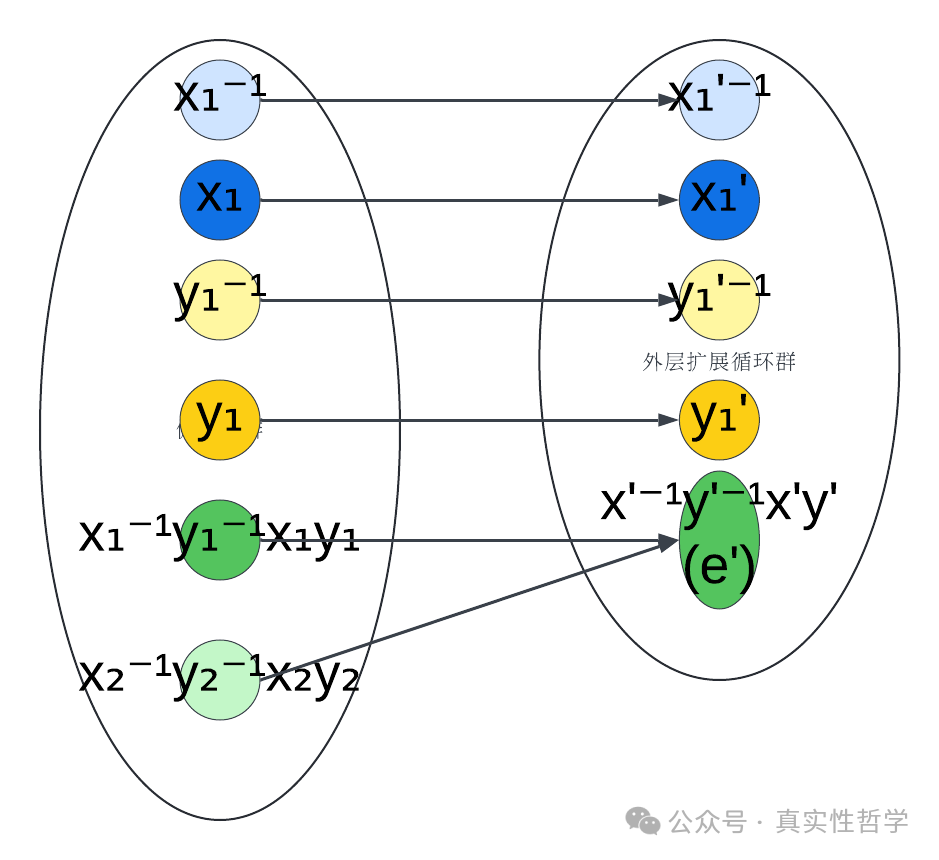
如上图,因为循环群是可交换群,所以伽罗瓦群的交换子x⁻¹y⁻¹xy同态映射到外层扩展循环群的像x'⁻¹y'⁻¹x'y'是单位元e。
(因为可交换,所以x'⁻¹y'⁻¹x'y' = x'⁻¹x'y'⁻¹y' = e)
即伽罗瓦群的所有交换子都在伽罗瓦群与外层循环群的商群中,即伽罗瓦群的所有交换子都在内层合并扩展群,依次类推,伽罗瓦群的所有交换子都在每一级缩小的内层合并扩展群中。
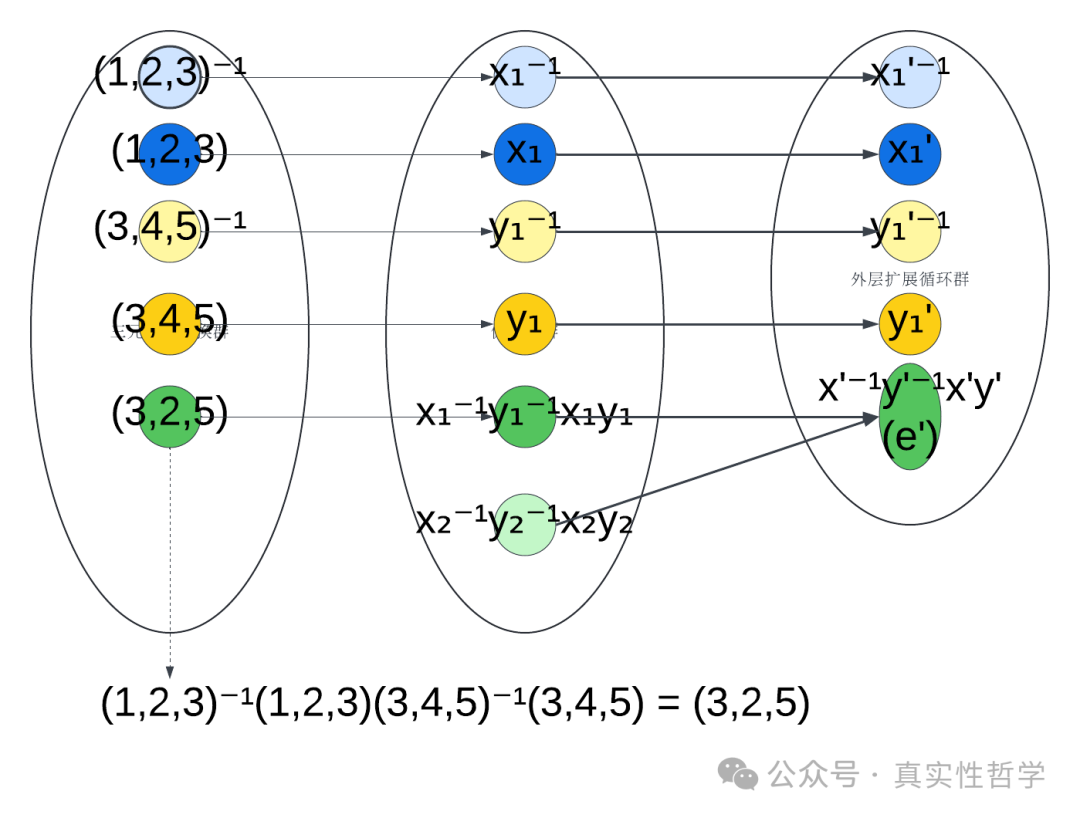
而我们在<伽罗瓦群论通俗导论 1 扩展的结构——1元5次方程为何没有通用的根式解?>,已经证明三元循环置换形成的交换子还是三元循环置换,如下
设x =(1,2,3), y = (3,4,5),
(1,2,3)表示对序号为1,2,3的元素做循环置换。
设序号为1,2,3的元素分别为a,b,c。
那么(a,b,c)在(1,2,3)的循环置换下会变为(c,b,a), 即位置1的a会到位置2,即位置2的b会到位置3,即位置3的c会到位置1。
x⁻¹y⁻¹xy
=(1,2,3)⁻¹(3,4,5)⁻¹(1,2,3)(3,4,5)
=(3,2,1)(5,4,3)(1,2,3)(3,4,5)
=(3,2,5)
即,三元循环置换形成的交换子还是三元循环置换,并且交换子能映射到所有三元循环置换。
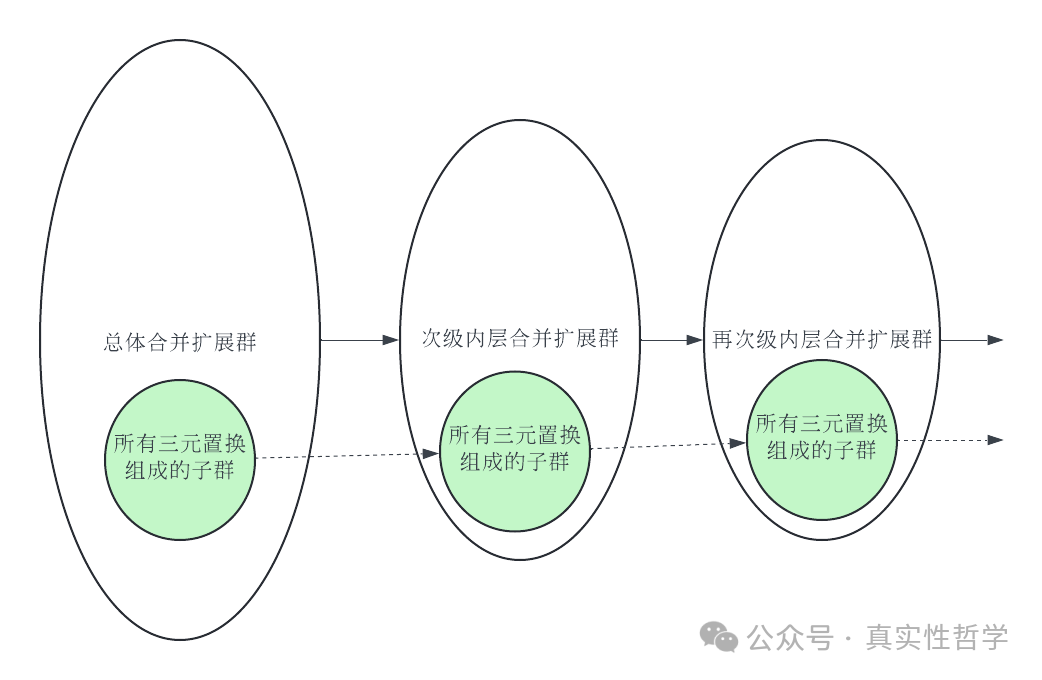
也就是说,所有三元循环置换会一直出现在逐层缩小的内层合并扩展群中,而包含所有三元循环置换的群不是可交换群,也就证明了该群无法由循环群逐层扩展而来,即此类1元5次方程无法用根式求解。
后记
得师指点,将伽罗瓦群论的迷雾又拨开了一点。
师曰:“黑暗再次袭来时,唯有哲学给人类带来慰藉和希望。只有想象是远远不够的,因为生命需要希望,或者说生命本身就是希望。”
时光匆匆流逝,唯师之透彻而不留一点迷雾的探索精神,时时触动了我,叮嘱我,跌倒,不要放弃,困顿,不要沉沦。在难得闲暇时,要继续探索。
师曰:“思想,要有自由探索的大无畏精神。”
吾尝疑惑,思想,何来大无畏?现渐渐有所领悟。若无思想的透彻,行动则盲目片面,勇敢则近于鲁莽。如无思想的自由探索的大无畏,则面对困境中的迷雾,往往苟且偷安,或者鲁莽侥幸。唯有思想的自由探索的大无畏,能冲破一切枷锁,在困境中寻找希望。
大无畏,是天崩地裂之际,也要冲上云霄的顽强精神!
或曰:又开始大放阙词、超雄附体了。
那么,就让我们一起来为新的生命与希望,脚踏实地、坚持不懈的大无畏地探索吧!

参考文献:
《Galois Theory 伽罗瓦群论》,Joseph Rotman
《Galois Theory 伽罗瓦群论》,Emil Artin
《真实与虚拟——后真相时代的哲学》,金观涛
《Elements of Mathematics 数学原本》,布尔巴基

















