从初中,到高中,到大学,到研究生,学了十年物理,“可谓十年生死两茫茫,不思量,自难忘。”(小朋友不要模仿乱用古诗词)
读了那么多书,上了那么多课,发现物理还是那么的有趣,那么地让人辗转反侧。

物理学是一门研究声、光、热、力、电的学科,它帮助我们解释生活中各种各样的现象,从苹果下落,到行星运行;从冰的融化,到水的沸腾。
这些从生活实际中总结提炼出的物理规律,又反过来指导和改变着我们的生活。大到火箭升空,宇宙航行,小到生活中的点点滴滴,不管你喜不喜欢,物理学已经浸透在我们的生活当中。
杠杆原理
“给我一个支点,我就能撬地球”,阿基米德的这句话大家都很熟悉,这里面蕴含的就是杠杆原理。
这个词听起来或许陌生,但是应用十分广泛。当我们用剪刀剪纸、用筷子夹菜、用秤称量时,都在使用杠杆。
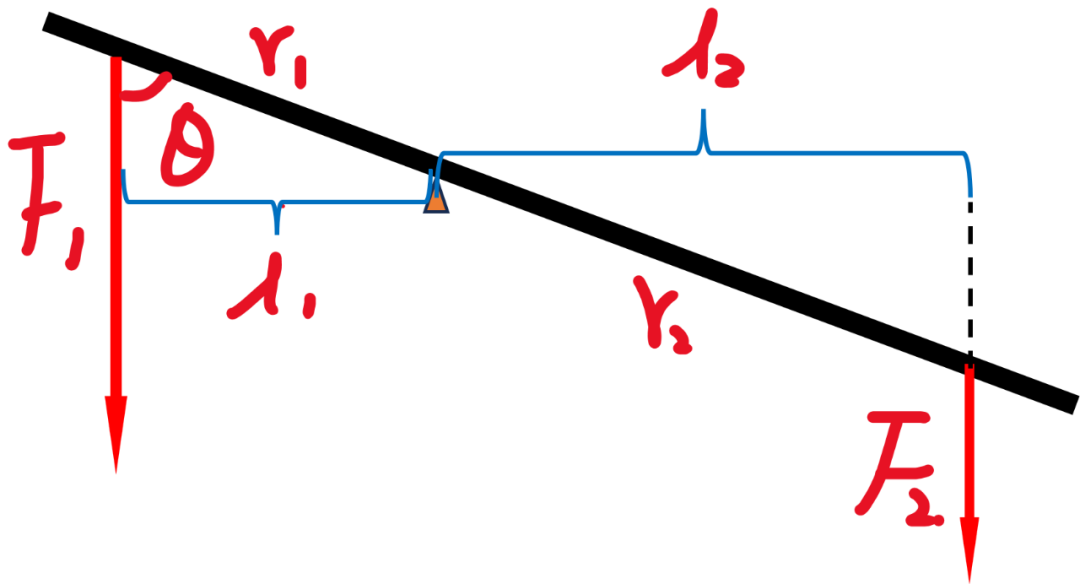
杠杆平衡条件为:
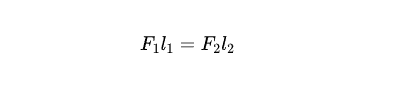
即动力*动力臂=阻力*阻力臂。
从公式中我们能看出,要省力就要费距离,要省距离就要费力,既要省力又要省距离是不可能的。(是不是从中悟出了点什么图片)
要利用杠杆带来的便利,关键是要找到一个支点。
根据杠杆平衡条件,杠杆也就可以分为等臂杠杆、省力杠杆和费力杠杆。
在一些需要省距离的地方自然就需要费力杠杆,比如船桨。刚刚参加过龙舟比赛的你是否注意到这也是一种杠杆呢?

图源:wikipedia
在这里,动力臂小于阻力臂,手对浆施加的动力比水对浆的阻力大,但是手只要移动很小的距离,浆就可以在水中移动较大的距离。费力杠杆是用力换来了距离。
随着年龄增长,我们发现力与力臂的乘积其实是一个叫做力矩的东西。
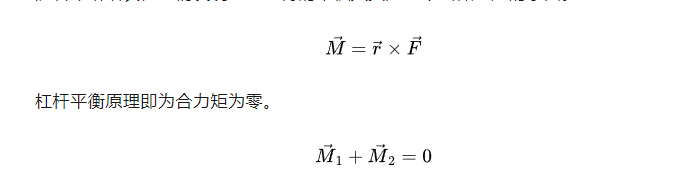
陀螺的转动,自行车的平衡,都与力矩有关。关于自行车平衡的原理,
在历经1935960小时,我们破解了自行车平衡的奥秘中,给出了详细的介绍。
对称性与守恒量
物理学中还有一个有意思的东西,就是对称性。
我们有着以对称为美的传统,大自然也喜欢对称的结构。宏观上,很多建筑和人为设计的东西都呈现出一定的对称性;微观上,原子结构,晶体结构也都呈现出某种平移或旋转对称性。

对称性在物理学的研究中有着举足轻重的作用。
物理学家最喜欢的东西就是对称,因为对称性可以降低系统的复杂程度,简化物理规律,这样看起来会更美,比如球形鸡。

图源:知乎
对称性往往对应着某一种守恒量。
例如,空间平移对称性对应着动量守恒;空间旋转对称性对应着角动量守恒;时间平移对称性对应着能量守恒。这些守恒关系都可以从拉氏量推导而来,这里不做过多赘述。
然而大自然并不总是对称的,当系统不再展现出某种对称性时,我们称之为对称性破却。对称性破却往往会带来新奇的物理现象。
电与磁
电磁现象有着悠久的历史。公元前600年左右,希腊人泰勒斯(Thales)就发现摩擦过的琥珀可以吸引羽毛等轻小物体的现象;在东汉时期,我国就有了关于“司南”的记载。

图源:wikipedia
在电磁学里面,“场”是一个很重要的概念。
在此之前关于力学的学习中,我们接触到了物体之间的相互作用力都是存在于直接接触的物体之间的。比如用手推木箱时,通过手和木箱的直接接触,把力作用在了箱子上。我们学摩擦力时也指出,两个接触面粗糙的物体之间有压力,且有相对运动趋势时,才会产生摩擦力。
但是电力(电荷之间的相互作用力)、磁力(如磁铁对铁块的吸引力)、万有引力这几种力的作用方式却有所不同。这几种力可以发生在相隔一定距离的物体之间,彼此之间不需要接触。
这并不是说明这些力是“超距作用”,而是由相应的“场”来作用的。凡是有电荷的地方,就会在自己周围的空间激发电场,电场对处在其中的任何其它电荷都有作用力,这就是电场力;磁场也类似,磁极或者电流会在自己周围的空间激发磁场,对于处在磁场中的任何电流或者磁极都会产生作用力。所以电场力和磁力其实是一种“近距”作用。

图源:wikipedia
电和磁不是彼此独立的,而是相互联系的一个整体。尽管在很长一段时间里,电学和磁学是相互独立发展的,但是经过一些重要的发现,人们将电和磁联系了起来。
1731年,一位英国商人发现,雷电过后,他的一箱刀叉竟然有了磁性;1752年,富兰克林发现莱顿瓶放电可以使缝衣针磁化;1820年,奥斯特在一次讲课中,把导线沿南北方向放置,通电后发现指南针发生偏转,发现了电流的磁效应;1831年,法拉第发现了电磁感应现象。
由此,电场和磁场被统一了起来,统称为“电磁场”。并且,人们还证明了电磁场是可以脱离电荷和电流独立存在的,它和实物一样具有能量和动量。场与实物只是物质存在的两种不同形式。
矢量和叉乘
在电磁学的学习中,由于电和磁的相互作用,出现了一堆的左右手定则:
判断通电导线磁场方向的右手螺旋定则,判断通电导线在磁场中受力的左手定则,判断洛伦兹力方向的左手定则,判断导体切割磁感线产生电流方向的右手定则。
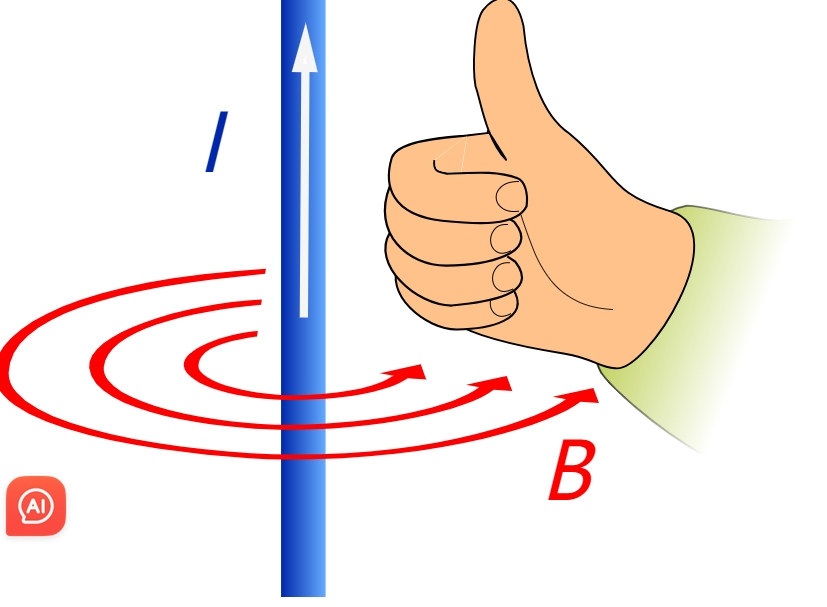
图源:wikipedia
小编记得这些定则被老师形象地总结为“左力右电”。尽管上学时没少背,但过去了这么多年,现在已然是记不住了。
年纪大一点,接触了叉乘,发现这些左右手定则原来都可以被统一到叉乘里面。
点乘和叉乘都是矢量的性质。
在学习速度的时候我们就学过矢量是既有大小又有方向的量,用一个箭头表示。
利用矢量的三角形法则进行矢量的加减运算。
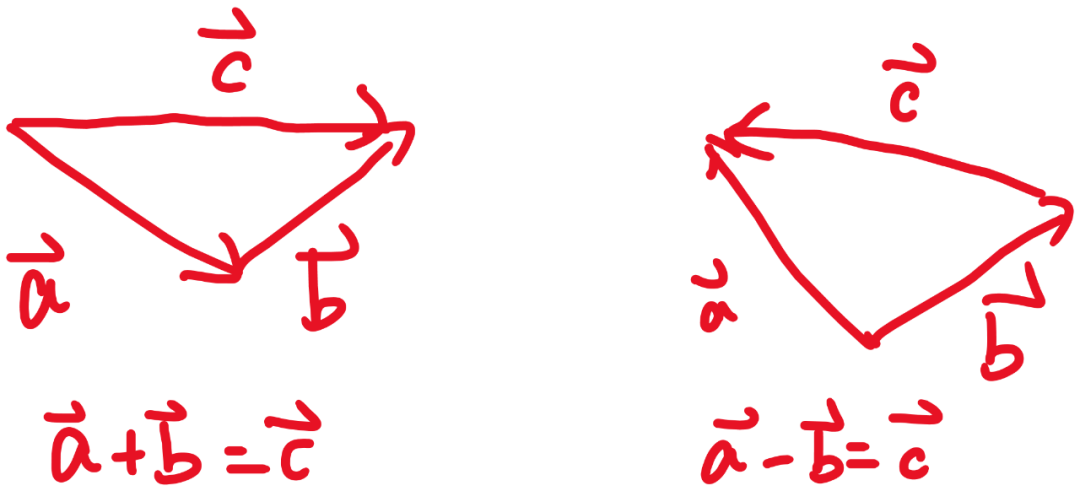
矢量相加就是把各个矢量的箭头首尾相连,从第一个矢量的尾指向最后一个矢量的头的矢量就是和矢量;矢量相减是把两个矢量尾放在一起,从减矢量的头指向被减矢量的矢量是两矢量的差。
两矢量点乘得到一个标量,标量只有大小没有方向,就是一个数。标量的运算为:
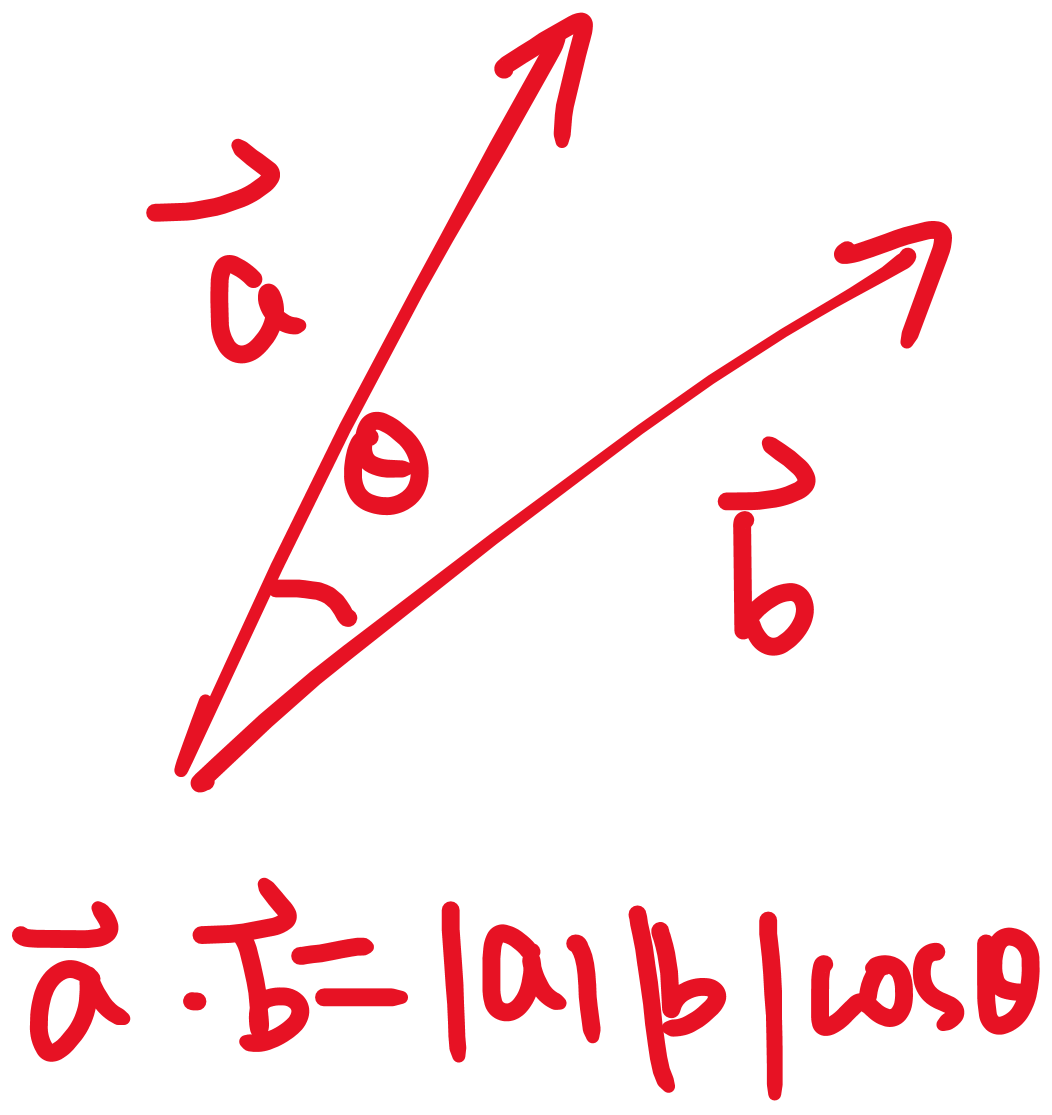
其中 |a|,|b| 为矢量的大小。
两矢量叉乘得到的还是一个矢量,
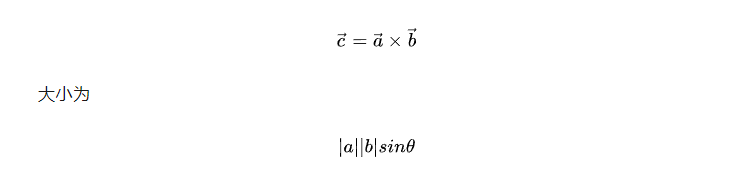
方向垂直于这两个矢量的方向,可以用右手来判断。四指从a矢量的方向弯向b矢量的方向,大拇指的放久就是c矢量的方向。因此在叉乘中交换前后两个矢量的位置,就会颠倒结果的方向。
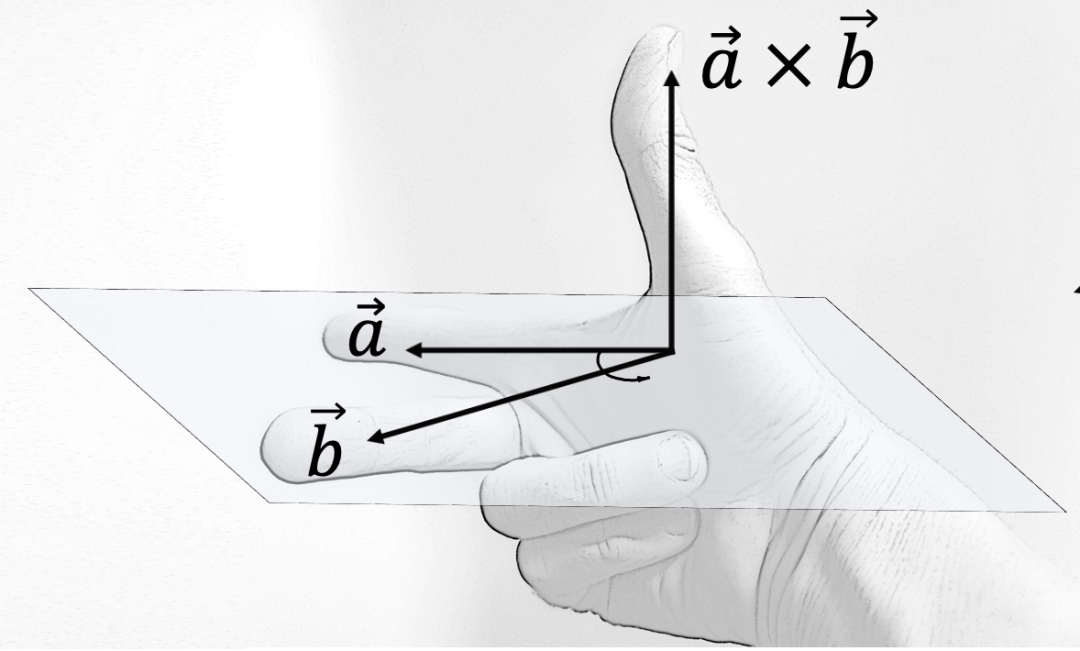
图源:wikipedia
有了叉乘的概念,就可以把左右手定则都用叉乘来表示。
带电粒子在磁场中运动所受洛伦兹力为,
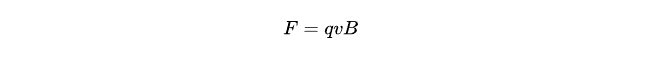
方向要用左手定则来确定,假设磁场方向垂直纸面向里,粒子向右运动,伸出左手,让磁场穿过手心,四指指向粒子速度方向,那么大拇指方向就是洛伦兹力的方向。

这是我们之前所学的知识,现在有了叉乘的概念后,摇身一变,它成了
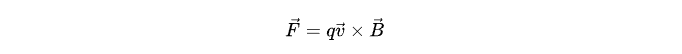
伸出右手,四指由速度方向弯向磁场方向,大拇指方向就是洛伦兹力方向,竟然完美一致。
有了叉乘的概念,就把矢量的大小计算和方向判断在一个公式中统一了起来,虽然计算上没有变简单,但是看起来是在简洁了不少,写起来也省事了很多。
电磁学博大精深,各种矢量叉乘、点乘、积分、微分的运算和各种电磁有关的概念学的小编晕头转向,乐此不疲。
电子自旋
跨过了经典力学的大山,终于来到了量子力学的门前。波函数的统计诠释已经是一个很费解的概念,电子又多了一个自旋。
小时候只知道电子具有电荷和质量,长大了才知道原来电子还有自旋。电子自旋是在量子力学发展之后才发现的电子的一个新的自由度,它是电子的一个内禀属性,并没有经典对应,与自旋对应的磁矩为内禀磁矩。
Uhlenbeck和Goudsmit根据碱金属光谱的双线结构和反常Zeeman效应提出了电子自旋的概念。电子自旋并不是一个机械自转,因为在这一假设下,电子的旋转速度会超光速。
Stern-Gerlach实验直接证实了电子具有自旋,且电子自旋只能取分立的两个值。
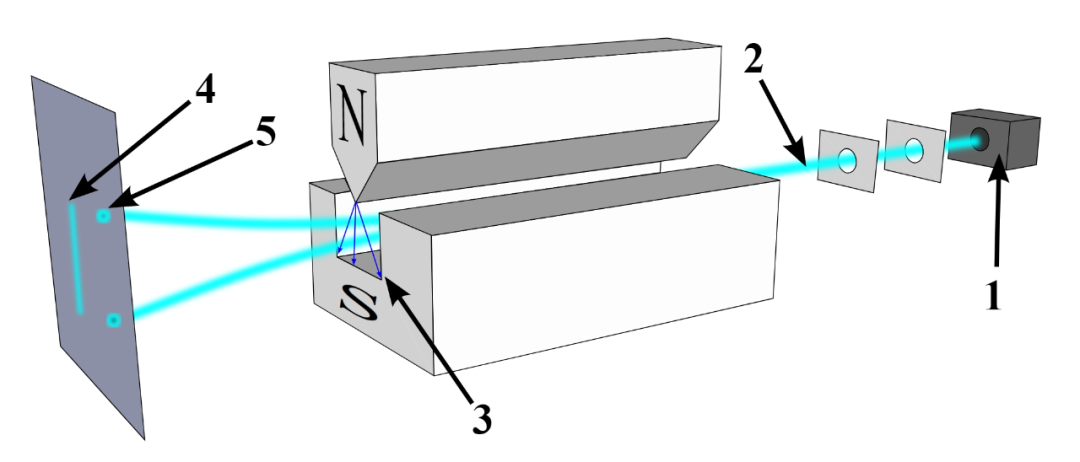
图源:wikipedia
实验其实很简单,一束银原子进入磁场,按照经典物理,观测屏上的结果应该如4所示,但实际观察到的是5所示的结果,原子束一分为二,说明电子的磁矩沿竖直方向是量子化的,只能取两个值。这就说明电子还具有一个新的内禀自由度——自旋。
电子自旋的发现对量子信息和量子计算的发展产生了深远的影响。
从初中到大学,从经典物理到量子物理,物理学的知识包罗万象,解释着世界,也在改变着世界。尽管学习的过程中会遇到重重困难,但是物理之美一直在吸引着我们继续探索,永不停息。
参考文献:
1、《量子力学》,曾谨言,科学出版社
2、《电磁学》,赵凯华,陈熙谋,高等教育出版社

















