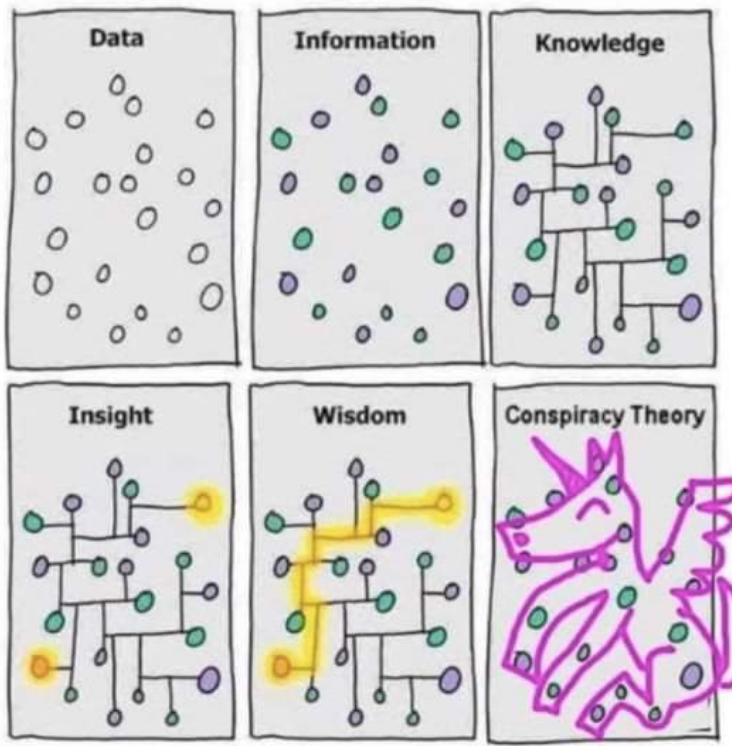
TLDR：这篇综述讨论了如何通过多种降维技术揭示认知科学中的潜在表征空间，并探讨了选择适合研究目标的嵌入算法时需要考虑的关键因素。看完后发现，除了图结构、排序数据的降维让人印象深刻外，其它部分似乎缺乏新意。许多内容（比如模型表现、如何选择模型）虽然重要，但在讨论中没有带来新的洞见，反而略显乏味。

DOI：10.1016/j.tics.2024.07.005

1.认知科学为什么需要多维空间

认知科学常常面临一个核心挑战：认知表征无法直接进行观测。为了揭示大脑如何处理信息，科学家们通过分析可观测的数据——包括文本、神经影像、神经网络模型，人类行为表现——来推断这些潜在（latent）的表征空间。

这些潜在空间不仅揭示了大脑如何组织和处理信息，还能够回答一些古老的哲学问题，比如“两个不同的人是否以相同的方式感知红色？”更重要的是，模型化的表征还能揭示人们注意到什么、忽略了什么。例如，经验丰富的皮肤科医生能够迅速识别出恶性皮肤病变，而新手可能完全察觉不到这些诊断特征。

提取潜在维度的方法种类繁多，统称为编码算法（encoding）或嵌入（embedding）算法，常用的有主成分分析（PCA）和t-SNE等。这些算法尽管目标相同，但在数据输入类型和输出维度的属性（如预测性能、转换类型、可解释性和紧凑性）上存在显著差异。因此研究者需要根据具体研究目标选择合适的算法。

2.可观测数据映射到潜在空间产生了什么变化

在可观测空间中，每个维度都与现实中的物理特征紧密相关，例如皮层厚度等可量化的特征。这些维度帮助我们理解和测量现实世界中的现象。然而，当我们将这些可观测数据映射到潜在空间时，维度的意义发生了根本性的变化：a. 新的潜在维度并不一定对应于我们能够轻易解释的全局性特征; b. 这些潜在维度并不一定存在于现实世界中，它们是从输入数据中推断出来的潜变量。优秀的潜在维度是认知模型的核心。

3. 选择嵌入算法时需要考虑的关键因素

不同的算法优化的属性各不相同，因此没有一个单一的潜在空间可以被认为是绝对正确的。相反，最合适的潜在空间应该是最契合研究问题的那个。例如，Big Five人格量表和HEXACO量表都提供了描述人格特质的低维度空间，但HEXACO在预测道德和伦理行为方面可能表现得更好。

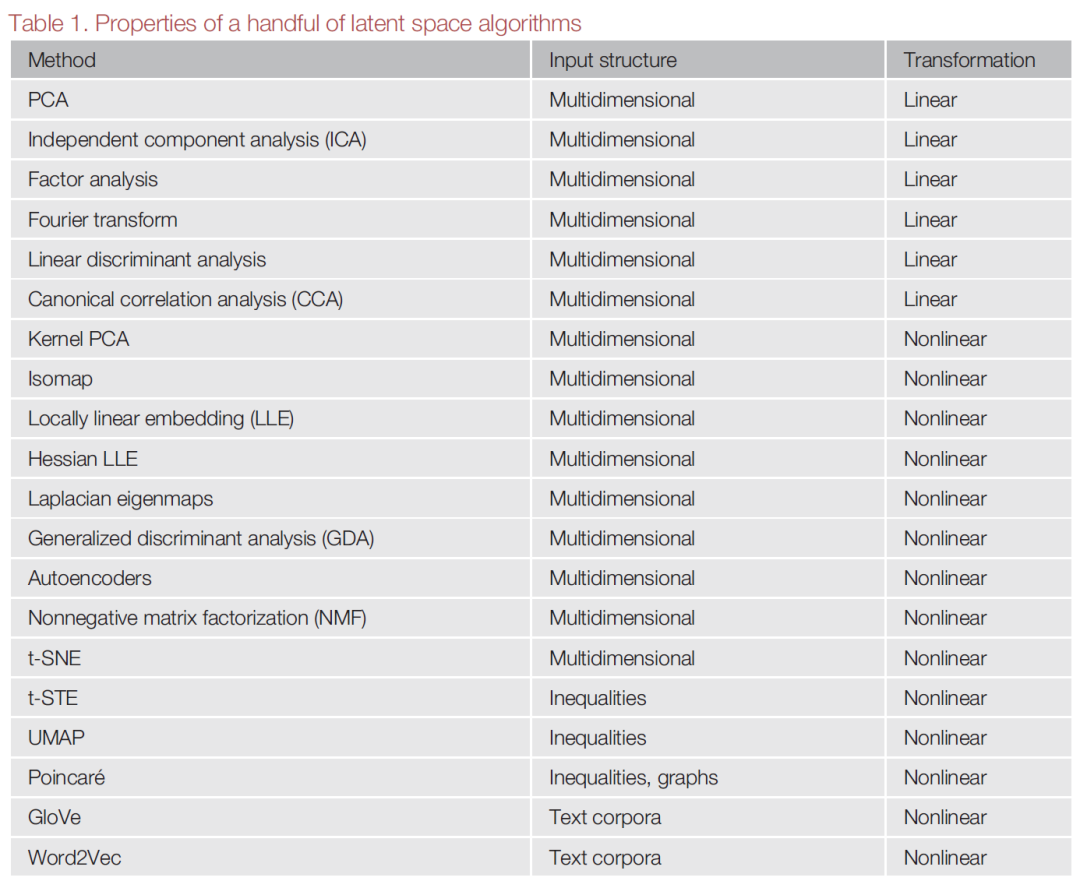
选择嵌入算法时需要考虑五个关键因素。首先，在输入方面，需要选择适合输入数据结构的算法。其次，在输出方面，不同算法优先考虑的潜在空间属性有所不同，这些属性包括：预测性能、转换类型、可解释性和紧凑性。表1👇总结了一些常用嵌入算法及其属性

3.1 输入的相关因素

主要包括三个需要考虑的因素

数据源：不同的数据源会对后续的分析和嵌入算法选择产生显著影响。

数据预处理：预处理步骤的质量和方式直接影响到最终的潜在空间表示，因此在进行数据预处理时需要特别谨慎。

数据类型：输入数据的结构形式也是一个重要的考虑因素。数据可以以多种形式存在，例如，作为一个多维数据表（如PCA处理的多维数据），一组序数关系（如人类偏好判断），一个节点和边的图结构，或大规模文本数据。数据类型的选择将影响嵌入算法的选择，因为不同的算法在处理不同类型的数据时有着不同的优势和局限性。

数据的类型不仅限于我们熟悉的数值数据，还可能是：

分类/排序数据（图1E）。一个常见的数据来源是通过收集人类的相似性判断来获得的（例如，刺激Q比刺激B更像刺激A）。针对这种类型的数据，存在一系列多样化的嵌入算法，它们能够将这些序数相似性判断转换为多维表示，其中每个刺激都在潜在空间中表示为一个点。这些算法中的许多没有正式名称，但通常归类于多维尺度法或心理嵌入方法。推断出的潜在维度可以量化“心理距离”的概念，即在潜在空间中，相似的项目会出现在彼此接近的位置（如图1E所示）。类似的嵌入算法也应用于其他类型的非数值数据，例如分类混淆矩阵（categorization confusion matrices）、成对评分（pairwise ratings）、找出异类的判断（odd-one-out judgments）、排列数据（arrangement data）以及非人类的实验范式。

文本语料库（图1F）。嵌入算法还可以处理文本语料库，从而生成多维的词嵌入和句子嵌入。词嵌入算法统计一对词语在指定窗口内共同出现的频率（如图1F所示）。在相似上下文中共同出现的词语通常具有相似的意义。

图结构（图1D）。图结构可以嵌入到多维空间中。例如，通过利用双曲空间的属性，层次图可以嵌入到多维空间中，相比欧几里得空间，在建模层次数据时，双曲空间往往需要更少的维度。一些行为数据（如气味）被证明可以很好地用双曲空间描述。

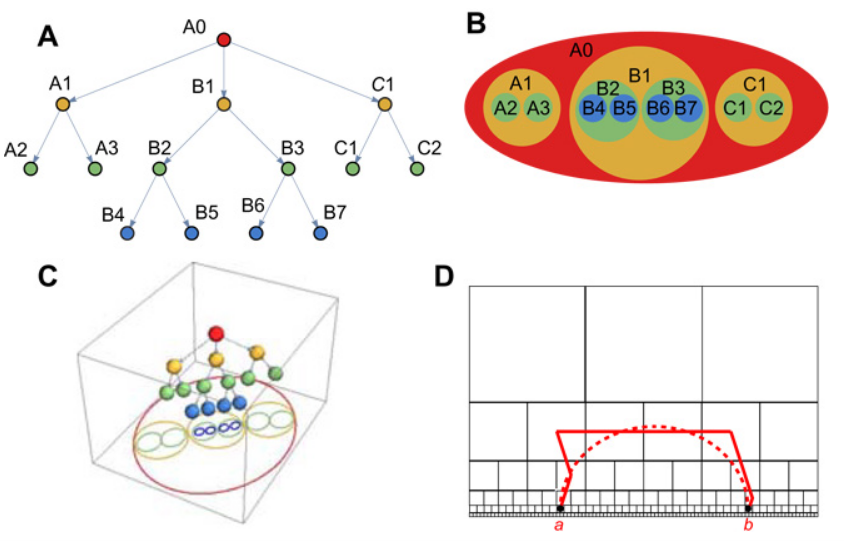
（Hyperbolic geometry of the olfactory space）

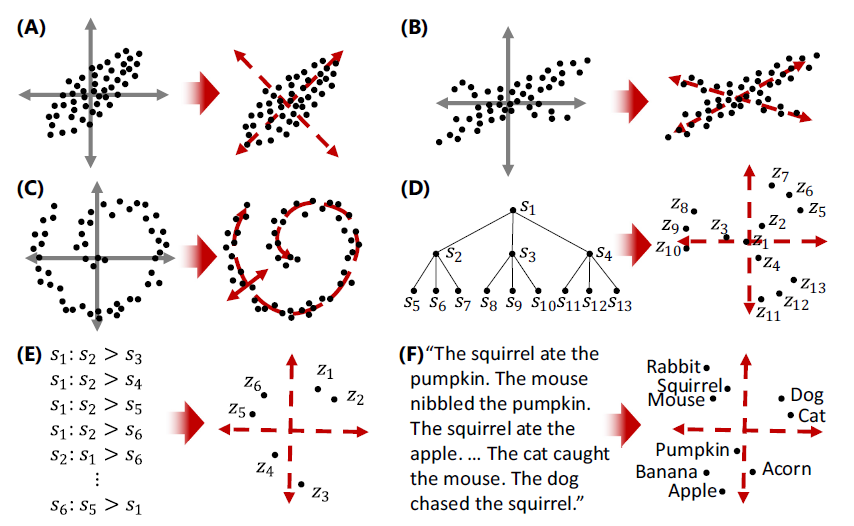
图1展示了通过不同数据集推导出的六种不同形式的潜在维度，涵盖了从线性到非线性、从多维数据到文本语料库的广泛应用。

图1A显示了通过主成分分析（PCA）得到的线性且正交的潜在维度，这些维度彼此独立，不存在相关性。

图1B则展示了独立成分分析（ICA）生成的线性但非正交的潜在维度，允许各维度之间存在一定的相关性。

图1C展示了通过非线性方法（如ISOMAP、t-SNE或UMAP）推导出的潜在维度，这些维度在原始空间中呈现出弯曲和扭曲的形态，用于捕捉数据中的复杂非线性关系。

图1D则展示了从层次结构图中推导出的潜在维度，这些维度被嵌入到双曲空间中，以更有效地表示层次结构。

图1E描述了基于序数相似关系推导出的潜在维度，展示了如何在心理距离的概念下，将相似的项目表示为彼此接近的点。

图1F展示了通过分析文本语料库推导出的潜在维度，基于词语的共现频率，在多维空间中表示出词语之间的相似性。

整个图1全面展示了不同嵌入算法如何生成各自独特的潜在维度，以及这些维度在揭示数据结构中的重要作用。

3.2 输出的相关因素

模型表现：指的是嵌入算法能保留输入数据关键信息并进行有效泛化。

转换类型：转换类型可以通过嵌入转换的线性程度和维度变化来描述。常见的线性转换方法包括PCA、ICA、傅里叶变换、因子分析和基于张量的降维方法。对于线性方法，降维通常涉及识别解释方差最多的一组潜在维度，并排除剩余的维度。常用的非线性降维算法包括ISOMAP、t-SNE、UMAP和各种自编码器。其他非线性降维算法还包括核方法、局部线性嵌入、拉普拉斯特征映射、Hessian特征映射和局部切空间对齐。非线性降维算法通常假设数据并非均匀分布，而是分布在较为连续的曲面（即流形）上。非线性转换（如t-SNE）允许新维度描述一个截然不同的空间，可能在原始空间中扭曲和转动。

可解释性：可解释性分为两种形式。强可解释性指的是每个维度都有独立于其他维度的清晰解释。强可解释性可以理解为全局可解释性：无论在维度的哪个位置，这种解释都适用。相比之下，一个维度可能只有局部可解释性：即维度的解释随着你沿着维度逐步移动而变化。图2帮助我们理解在不同的分析和建模场景中，选择何种类型的潜在空间是最合适的。

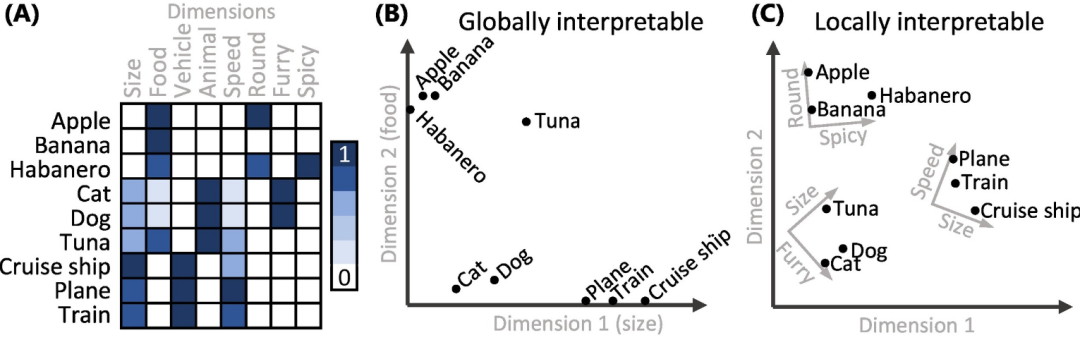
图2展示了不同类型的潜在空间及其在可解释性和维度变化上的差异。在全局可解释的潜在空间（图2A）中，每个维度都有明确且一致的含义，无论在空间中的哪个位置，这种解释性都保持不变，这对于建模和分析非常有用。相比之下，局部可解释的潜在空间（图2B）显示，维度的解释随着位置的变化而变化，虽然在某些局部范围内具有清晰的解释，但在整个空间内可能会有所不同。这种情况在处理复杂、非线性数据时较为常见。非线性嵌入的潜在空间（图2C）则展示了数据在更复杂的结构中分布的方式，维度的含义可能随着位置变化而剧烈变化，虽然它能更好地捕捉数据中的非线性关系，但维度的解释性较弱。

紧凑性：研究者可能会选择一个低维度且局部可解释的空间，或是一个高维度且全局可解释的空间。虽然这两种方法可能同样适合输入数据，但它们恢复出的维度数量会有所不同。

作者提出进行内在维度性分析（比如使用常见的碎石图）。内在维度性（Intrinsic Dimensionality）是指数据集在某种意义上最小的必要维度数，能够用来描述数据的核心结构或特征，而不丢失重要信息。例如，使用PCA分析某个数据集时，你可能会发现，前两个主成分解释了几乎所有的方差（例如，99%以上），而第三个主成分解释的方差非常少。这表明数据的内在维度性是二维的。

4. 比较和选择嵌入空间

在比较和选择嵌入空间时，研究者需要权衡不同算法的特性，直接比较候选空间可以揭示它们之间的相似性和差异，进而识别出哪种空间更适合特定的研究目标。通过评估嵌入空间在下游任务中的表现，可以间接比较这些空间的优劣，但需要注意嵌入坐标与可观测行为之间的映射过程。最终，选择最合适的嵌入空间应基于对比多种方法的结果，并考虑特定的研究需求和数据特点。

Outstanding questions

大脑在多大程度上在维度空间进行运算？

大脑是否同时使用不同类型的维度空间？一种可能性是，不同脑区的表征空间根据功能和情境的不同而有所差异。

大脑的维度空间是否可以随着任务环境的变化而变化并按需组装？