在数学的世界里，数论问题因其深奥和复杂性而闻名。这些问题往往隐藏着超出直观理解范围的深层次结构。然而，通过一种全新的方式来表示“数字”，我们可能找到了探索这些难题的新钥匙。看下面的问题：

这些数字：210，720，175560 和17297280有什么共同点？如果你回答说它们都以零结尾，那你是对的，但更重要的是，它们是唯一已知的可以用两种不同的连续整数序列进行因式分解而且两种方式之间没有共同的数字，

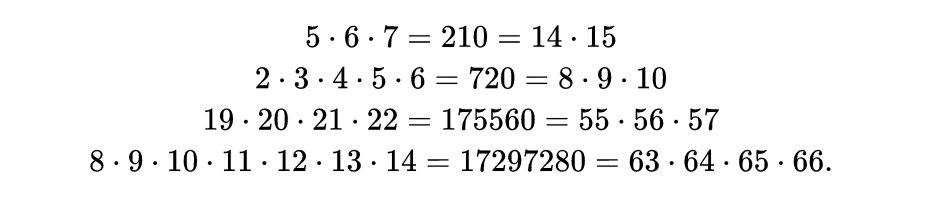
数字5040就不满足条件，因为两种方式都包含了7

这引出了一个问题：是否还有更多这样的数字，如果有，我们如何找到它们？虽然我没有答案，但我希望通过这个问题展示为什么数论很难。

既然这个问题涉及因式分解，我们必须从算术的基本原理开始，根据算术的基本定理，每个大于1的整数都可以唯一地表示为素数的乘积。最早的证明可以追溯到欧几里得的《几何原本》。但我这里想说介绍的是一种新的思路，一种将数字的素数分解转换为一种几何和视觉模型的方法，一种新的表示数字的方式，

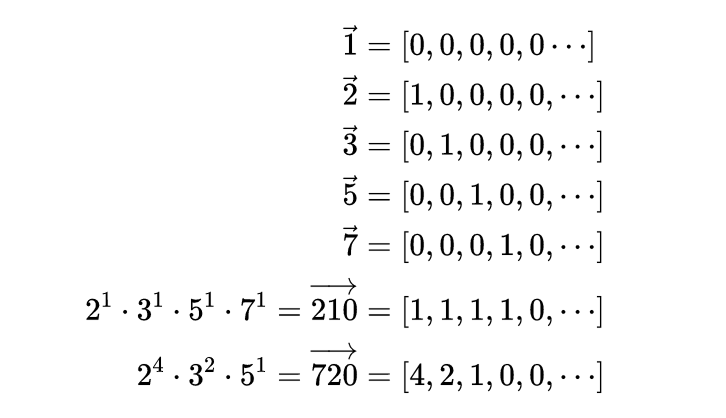
我称之为因子空间（factor space），一个高维的半模，每个素数都有自己的维度，我们可以用素数幂的列表（2,3,5,7....）来表示自然数，例如210的因子是2^1、3^1、5^1和7^1，因此因子空间的前4个元素都是1，从视觉上可以将这些视为指向空间的箭头或向量。因此，我们用箭头表示这个空间的成员，代表它在这个空间中的数字。

在这个空间中，有两个关键操作（运算）：加法和缩放。

加法的规则是将元素相加。并生成对应于乘积的向量。例如，取2向量和3量，并将向量的每个元素相加，得到一个对应于数字6的向量，即2和3的乘积。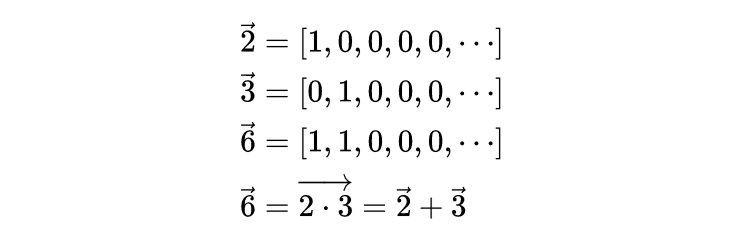

我们注意到，1向量不会对加法有什么影响，即任何数字向量与1相加的结果都是这个数字向量本身，这对应于数字乘法运算中的“乘以1而不改变结果的事实”。

要缩放一个向量，我们将每个元素乘以所需的标量，产生一个由该标量指数化的向量，如我们在4的例子中所见，

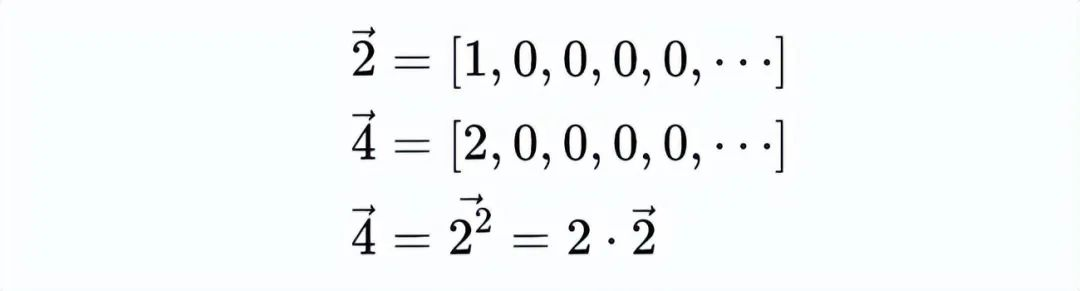
从几何上看，加法和乘法可以通过下面的图片来描述，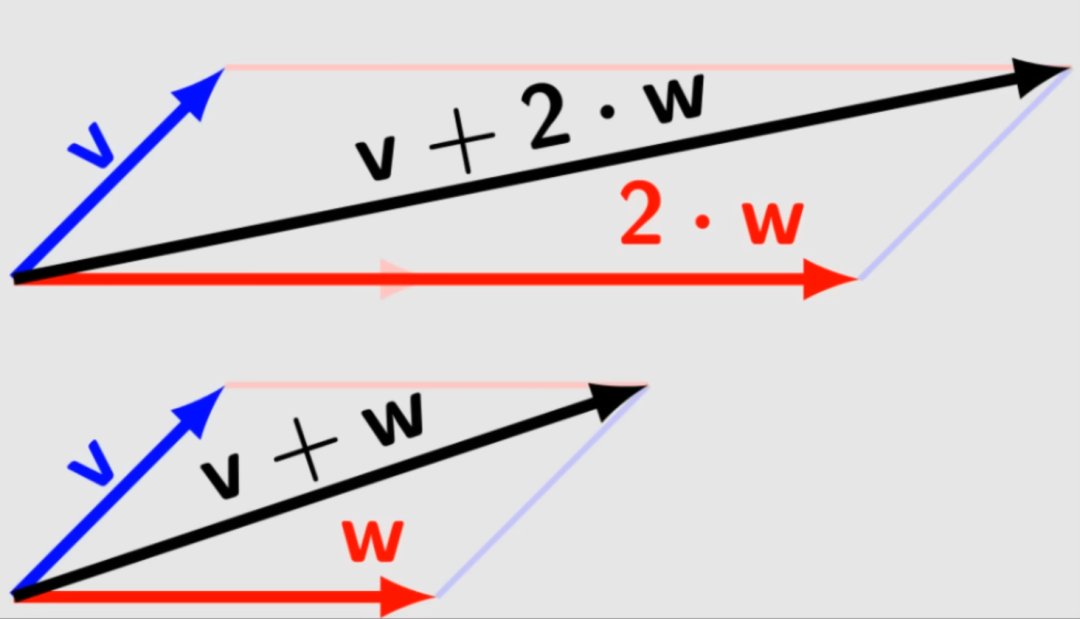

我们可以通过改变长度而不改变特定向量的方向来缩放向量，这种结构在许多方面都非常有用，例如，为了寻找数字m和n的最大公约数（GCD）和最小公倍数（LCM），只需要求这两个数的因子空间中对应数的最大公约数和最小公倍数：

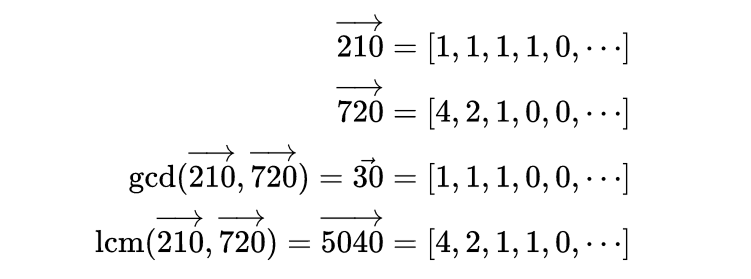
这也产生了一个平凡的证明，即最小公倍数乘以最大公约数得到了原始两个数字的乘积，

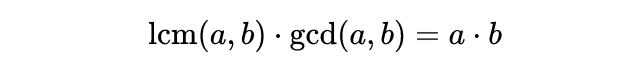
证明：

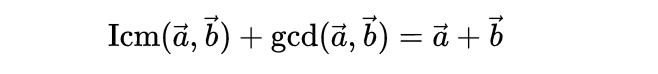
因为每个向量的每个分量在每种形式中都被计算了一次，所以

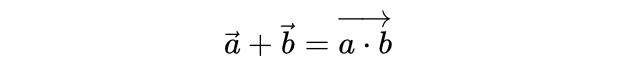
那些熟悉线性代数的人可能会将这视为基础的变化，我之所以特别讨论这些运算，是因为最大公约数可以揭示两个数字是否互质，这是因子空间中垂直箭头的几何意义。我们关心垂直向量是因为我们关心的许多重要的映射在数论中是乘法函数，

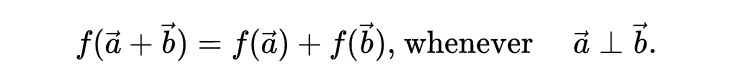
例子包括欧拉的totient函数 ϕ，莫比乌斯函数 μ，除数函数 σ_k，以及拉马努金的 τ 函数。

像这样保持结构的映射非常好，如果失去了这种保持结构的元素，我们很快就会迷失在深渊中。也许最简单的不保持这种结构的映射是后继函数，定义后继函数：

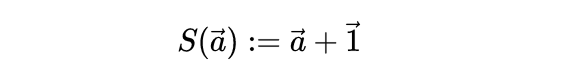
而：

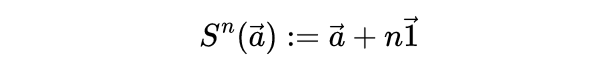
从  开始，连续应用后继函数S函数直到 1：

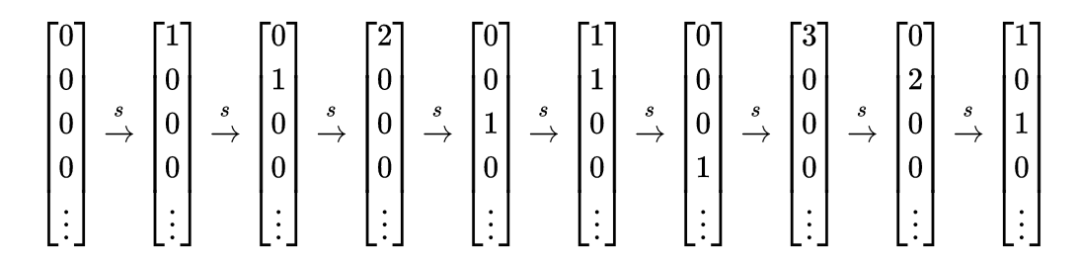
它在扰乱向量方面做得非常好。

通过取一个平方差，我们得到了这个非常奇怪的公式：

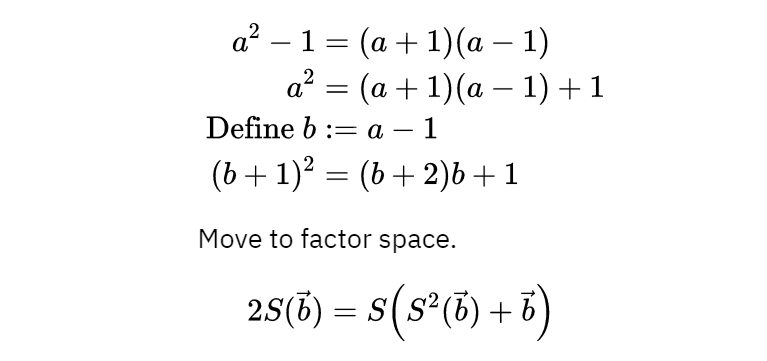
幸运的是，即使这仍然有点用处，我们知道一个数字及其后继是互质的：

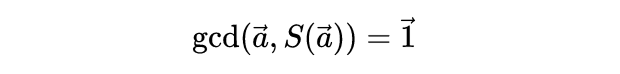
这意味着任何能够整除原始数字的数都不能整除其后继数字，这意味着s总是将一个向量移动到一个垂直的子空间，它还告诉我们，我们总是可以通过将S应用于已知素数的乘积来产生新的素数，这些素数必须存在于素数的新边界中，素数的无穷性公式就是这样表现出来的，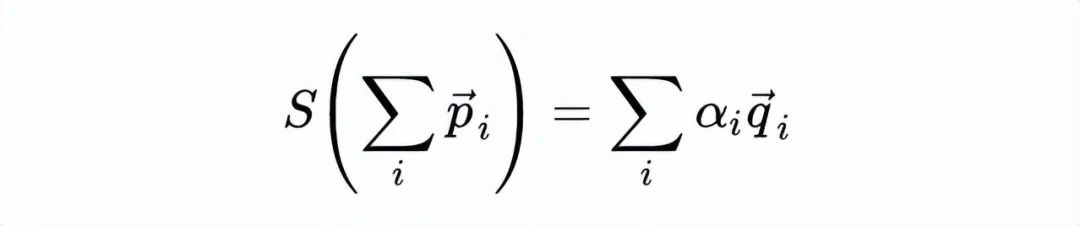

其中 α_i 是一些系数，q_i是另一列不同的素数。

我们将一系列素数的向量相加，应用后继，并从这个运算中得到一个不同素数的加权和。许多有趣的问题可以用这种符号表示，例如孪生素数猜想。

回到我们最初的问题，

可以用两种不同的连续整数序列进行因式分解而且两种方式之间没有共同的数字。

用自然符号表达为：

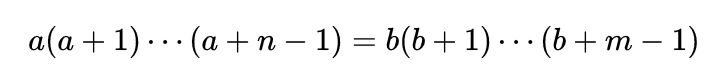
等价于在因子空间的

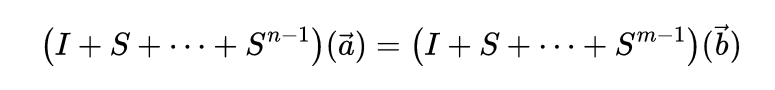
它询问当我们对后继函数进行几次迭代求和时会发生什么？数论家已经确定了特定情况下会发生什么，例如当m等于2或m=2n时，但没有通用的解决方案存在。

解决问题不仅需要处理由于多个素因子导致的复杂度（高维度），还要找到一个有效的方式来从一个数的因子分解转移到另一个，且这种转移不能太过复杂或费时（长度合适）。这要求我们找到一种在保持理论深度和计算可行性之间的平衡的方法。这种平衡是解决高复杂度数学问题的关键。

这可以通过考虑19到54的乘积等于23到57的乘积来看到，

由于这个方程要求两个高维度的路径相交，大多数解将需要较大的 m或 n 来允许 S的不连续性被抵消掉。例如：

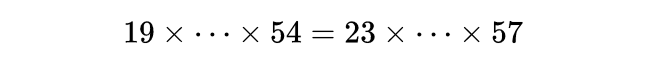
其中m=36，n=35。这主要是因为基于已知的简化解构建的高度重叠。

还有更多的解吗？也许有，但当前的技术和方法可能不够，需要通过科技进步和理论创新来寻找新的解。