高等数学，一个江湖上赫赫有名的传说。

神秘而又令人窒息，迷人而又让人懵逼。

为ta，你辗转反侧，彻夜难眠。

为ta，你六神无主，忧心忡忡。

它就像花园里一朵带刺的玫瑰🌹，你本欲上前采摘，又踌躇不定、战战兢兢。你欣赏它的美丽又怕它的尖刺居破你的手心。（居 vt. 四川方言🙄：扎/刺）

（原截图来自https://www.kankanews.com）

高等数学一直徘徊在大学最令人拙计的课程前三名。

甚至对于某些同学来说，是一直无法逾越的天堑。也似乎没找到什么神奇的密道可以通向它。

今天我要来讲讲那些高等数学劝退路人的瞬间。

看它是否是所谓的劝退大师，还是你可能没有找对学习方法。

鉴于这期仅针对路人初学者，本文只讲述那些入门级的问题。偏微分方程等请大家自行研究或请教隔壁韦神。😄

以下是高数劝退路人的迷惑瞬间：

劝退者1号:  求极限原理

劝退原因：翻书洛必达，合书洛丽塔。

（图片来自百度图片）

其实极限是相对比较简单的内容，但是不会就真不会。

不会就完全入不了高数的门。不要说正门，连厕...sorry 连侧门都进不了。😄

从这点来说属于伤害性不大，侮辱性极强。

而求极限原理的重要性还得从一期脱口秀节目说起。

节目里某211工科硕士徐志胜如是说：

（以上截图来自b站视频）

他这几句话来源于生活体验。在校园里，别人告诉他年轻人的机会是无限的，但他出来找工作时发现年轻人的数量也是无限的。😄

哈哈哈，不学点高数是不是连脱口秀也没法看了，大家还能不能一起愉快地玩耍了？

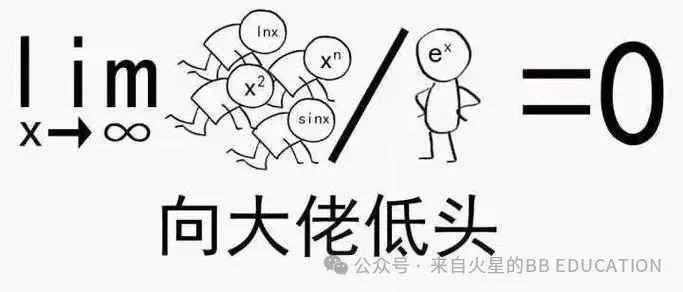
至于这个♾️比♾️等于0的问题（♾️为无限/无穷符号），

就不得不上我们传说中的洛必达法则了：

（截图来自百度图片）

洛必达法则主要适用于分子和分母函数均趋于0或二者均趋于无穷∞的情况（未定式）。而且前提是函数可导。

（原图片来自知乎）

鲁迅文学告诉你，此处“倒”通“导”，求导的导。

它体现了两者都趋于0或者趋于无穷∞时，极限有可能是一个常数 or ∞。哪个函数变化速度快哪个就能掌握主动权。而变化得快还是慢得看斜率，即导数（dy/dx 或 y′ ）。

就像两个函数在比赛，比如♾️/♾️类型，如果分子趋于∞的速度比较慢，而分母相对变化很快（例如指数函数eˣ），那么分子比分母的极限值则等于0。

我们回到脱口秀那句话：年轻人的机会是无限的，年轻人也是无限的。当年轻人的数量增长远超过机会时，极限也就差不多等于0了。

【注：上面分子求2阶导为常数，3阶导为0，分母指数函数无论求多少次导数都是eˣ。】

这种心情谁懂？😂

（图片来自百度百家号，来源：贵思教育集团）

。。。。。。

“无限比无限很有可能等于零”，这是多么富有哲理和现实意义的一句话。终于看懂了😉，喜提脱口秀自由。

另外，积分的发散和收敛也有求极限问题。所以极限是一个很基础也很重要的知识点。

劝退者2号：泰勒公式

截图来自百度图片搜索页面）

虽然Taylor Swift 很好看很友好，但是数学家泰勒显然路数不一样。

泰勒公式作为高数劝退者2号必然比1号更加不友好。😄

那么泰勒公式是什么？它是用来干嘛的？

其实它的目的就是将一堆奇奇怪怪的复杂函数转换为多项式函数。因为多项式函数是最简单的一类初等函数。

若函数f在x=a光滑，我们设一个多项式Pn(x)🟰

在所有次数为Ｎ或更低的多项式中，当x在a附近时，最近似于f(x)的便是多项式Pn(x)。

这条定理叫做“泰勒近似定理”。

因为是近似，所以Pn(x)又名“拼夕夕”（Pxx）（我自己瞎编的）。

如何验证拼夕夕类似于拼多多（即原函数f(x)）？

【验证方法：多项式等式两边求导】

可🉐：

当x=a时，多项式Pn(x)和f函数从零阶导到N阶导都相同。

即有一个近似的多项式函数可以替代原来的复杂函数。

或者说函数Pn 提取了f在x=a处直到n阶导数的所有信息。

其实真实的泰勒公式长这样：

（图片来自百度图片）

😆😆……学高数的同学们精神状态非常好啊。

😄下面这个公式更严肃一点。（这里把x0和a看做一样的就行）

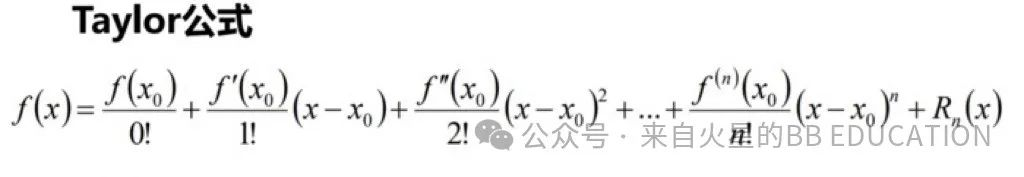
简写公式：

(以上截图来自bilibili.com）

我们可以清楚地看到这里比Pn多一个余项Rn(x)。这个余项又名n阶误差项，即真实的f(x)和近似的多项式之间的误差。

而如果要考虑这个余项的计算，则有好几种方法：

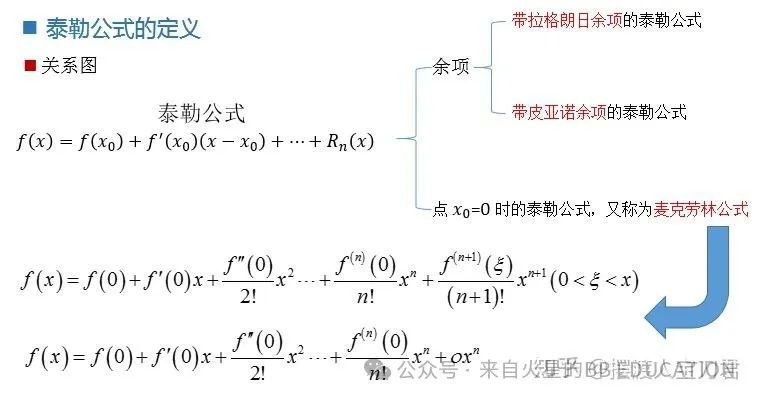
（图片来自知乎）

到这里好多同学已经懵了。

然而这些公式是不需要死记硬背的。只是看起来唬人而已，都是纸老虎。

比如有常用泰勒展开公式的表（a=0时的泰勒公式又称麦克劳林公式）：

截图来自知乎，来源：谁要学英语）

但是应试时一般会给个近似估计，比如n=2或者3：

（截图来自知乎专栏，来源：叶灵均）

其中O(x^n）为麦克劳林公式所带的皮亚诺余项。

大家愣着干嘛？鼓掌吧。打字不易啊。😄

下面请欣赏一张可以体现网友精神状态的表情包：

劝退者2号看似公式一堆，但并不需要怎么背，还是思维方式更重要。所以大家不要一看到长公式就产生畏难情绪。

（图片来自趣历史网站https://www.qulishi.com）

要是实在看不懂，应立即停止学习，进行科学性的周期性的膜拜大神的活动。

劝退者3号：一阶线性方程

劝退原因：式子复杂，长长长长长

闲来无事看网课，

发现弹幕一片愁云惨雾。😄

感觉才讲到一阶微分方程，就随机劝退了一more多路人。

可见微分方程的威力不容小觑。😄😆

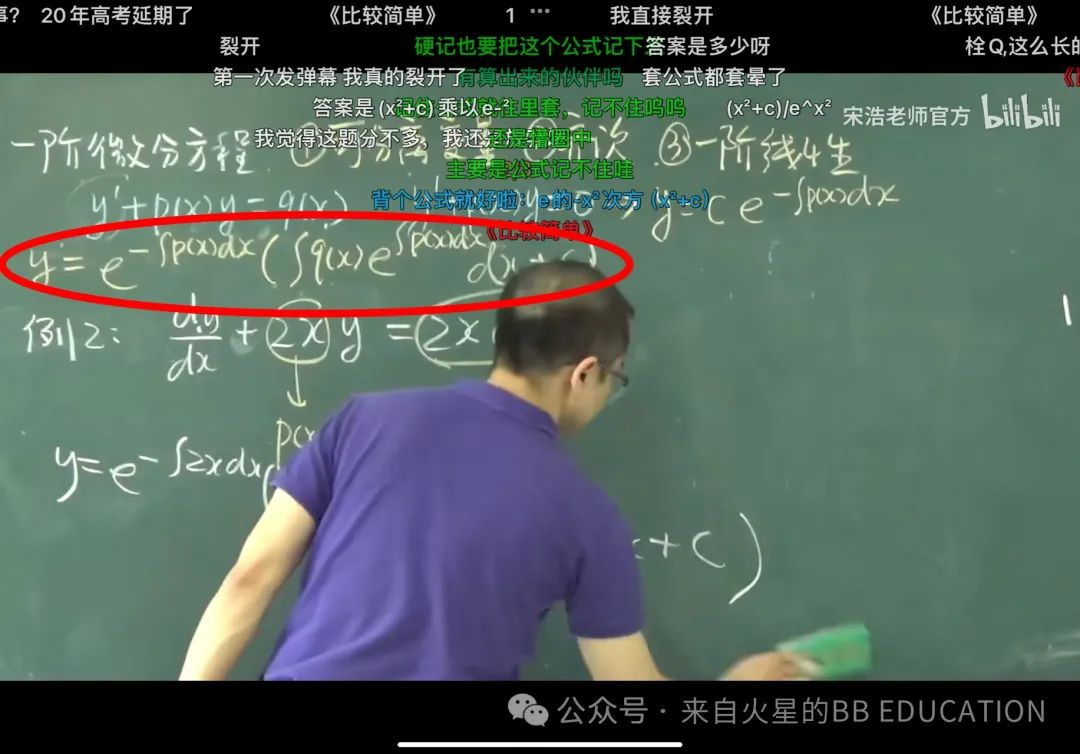
（截图来自bilibili.com）

上面是宋浩老师的《微积分》｜《高等数学》网课，内容是一阶微分方程里的一阶线性方程。

这个答案有没有可能只是表达得比较复杂，其实仔细思考根本没那么繁琐。

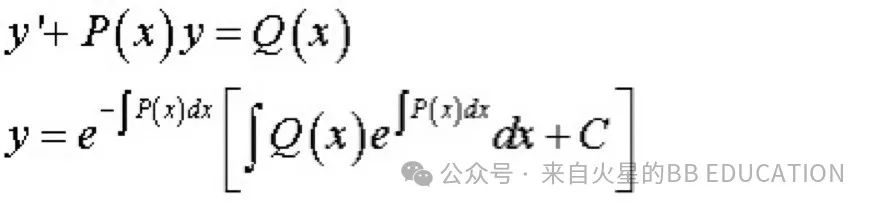
看下普林斯顿那本微积分教材，积分因子就是下面⬇️这个东东（很大一坨很难评）：

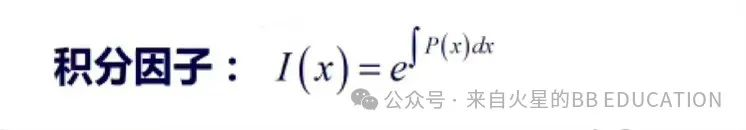
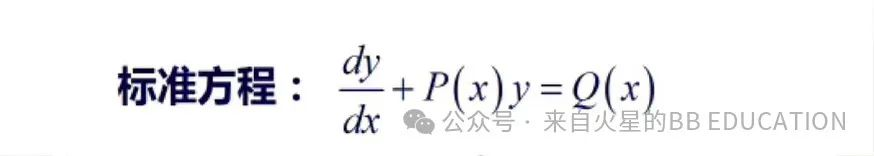
（以上截图来自百度知道）

然后在标准方程两边乘以这个积分因子（还是这一大坨）。

步骤如下所示：

将积分因子和y看成两个关于x的函数，用乘积法则操作。

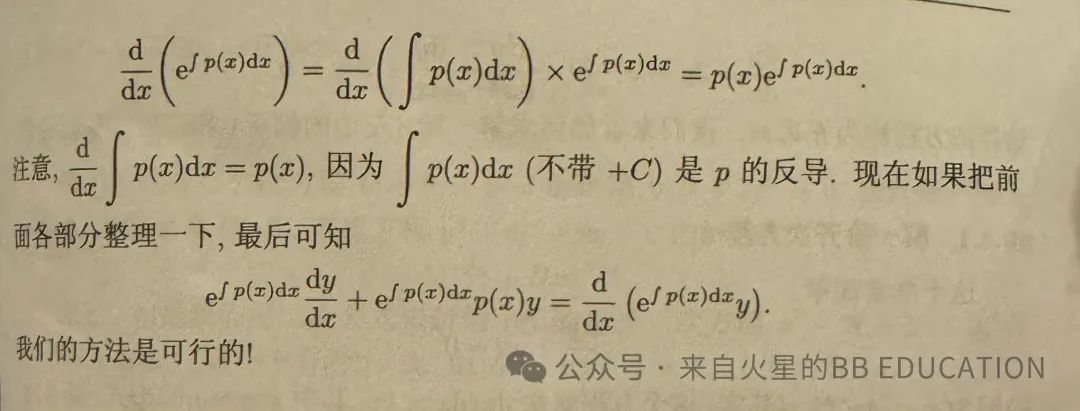
（以上截图来自普林斯顿微积分读本（修订版））

可证明这是O特么K的。😆

网课的推导过程也很清晰。

但是大家为什么懵，究其原因是不习惯看长的复杂的式子。

比如函数套函数，多套几个，就算只是在Excel里，很多朋友已经不想再看了，何况带入更复杂的数学公式。

但是如果你将这一大坨设为函数t（或写做t(x)），然后将t*y的值设为函数u……是否感觉一下就easy了。

正确的方法就是化繁为简，然后再重新带入那一大坨式子，ok，完成✅！

我这个写法比很多网课老师写得更简单明了。

但是大家要注意，图简便快捷有时候容易出错🤔，比如：

以上是我总结的《高等数学》上册的劝退迷惑时刻，说人话就是可能在初次学习中会遇到的重点和难点。

整体来说，高数（上）是比较简单的，微分方程也是入门级的。

希望大家不要被劝退，能坚持学完。你会发现收获满满。

困难？就像tan 90度，不存在的。