维特根斯坦的逻辑世界中描述了这样的一种复合命题：明天要么是下雨的，要么是不下雨的。在现实的表达中，这类表达是没有意义的，它虽然肯定是正确的命题，但却又好像什么都没有说，唯一引入的信息就是存在下雨这种天气。但维特根斯坦说这样的表述是非常重要的，虽然它没有什么告知什么可以价值判断趋向的信息，但是它却是表现我们语言世界结构的重要部分。

起初读到这部分的时候，是感觉很困惑的，没有价值但是却又作为框架一样重要，但是通过以下这个比喻就了解了。

下面的两个图是常见的迷宫游戏和迷宫游戏的解法：

迷宫游戏，从左下角出发到右上角：

上述迷宫的解法示意：

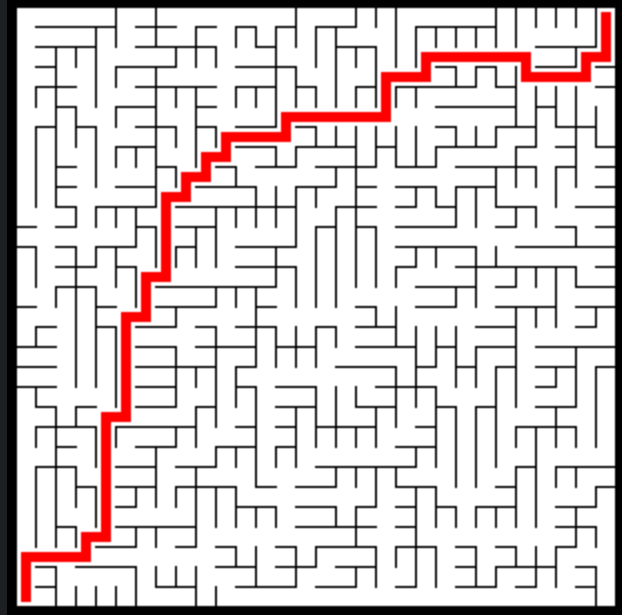
也就是说，如果从一开始定义了迷宫这个游戏，那么就必须要有可以穿过的道路，和不能穿过的道路。如果把可以穿过的道路比喻为对我们有价值的信息（明天一定会下雨或者明天一定不会下雨），那些不能穿过的道路是属于什么呢？现在假设把这些不能穿行的道路从地图上去掉，那整个迷宫的游戏（框架）就会崩塌掉，变成从A到达B的路径。一栋房子如果只有承重墙，那也肯定算不得一个房子。

所以那些看似不会传递消息的描述，恰恰是语言框架的基础，如果引入一个数学概念去协助理解的话，那就是语言本身也是有维度的，最小粒度的基本命题可以传递准确的信息（像A到B直线），而构成的复合命题却多加了一个维度（组成一个迷宫平面）。

讨论到这里的时候，就有一个疑问：那如果我们消除这个语言中的维度是否可行？回到日常生活的语言环境中来继续看这个问题：如果现在我有两个苹果，一个是青色的苹果，一个是红色的苹果，这个时候我管青色的苹果为青果，红色的苹果称为红果，将它们视为两个对象，这样定义下去，我可以用简单命题充满我的世界，在我的世界中，只要有一点点不同，就会被定义和区分，彼此的两个命题一定是完全独立的。（可以预见的就是：即使汉字再多，也难以穷尽我遇到的所有事件）。

所以必须建立一个框架，让语言可以在若干维度上自由的组合，形成一个巨大的多维方格来描述我们遇到的场景（颜色+形状+物体），这样的一个逻辑结构就可以描述几乎所有可见的物体，而不需要为每一种物体都起一个名字，这就是潜藏在语言中的结构。但如果语言这样定义，还存在一个问题，会出现一个维度组合，就是（颜色+颜色），（形状+形状）的组合，比如“红的蓝”，“方的圆”，这些明显是现实中不可能存在的事物，但是却存在于语言的逻辑世界中。

讲到这里时，又回到了小娃的语言世界中，在他理解的组合中，即使用“书摔倒了”，“狗狗嘎嘎叫”，也是没有什么问题的，至少从语言的逻辑去看，都是符合语法的，只是不符合现实。（随后，会补全维特根斯坦关于现实和语言是互为映射的部分）。

我们想象有这样一个巨大的村庄，里面如同迷宫一般，有无数条小路，从村子的一侧，走到另一侧，可能有很多条道路，也可能会遇到死路，但我们并不能完全将那些走不通的道路，从语言中舍弃掉，因为它们同样也是构成通路一侧的重要结构。这或许就是维特根斯坦所说的“虽然它们不传递任何信息，但是依旧是语言世界重要的结构”吧。

语言是我们建立的很伟大的交流工具，但它并不是完美的，虽然语言可以传递信息，但同样，也会形成很多符合逻辑的语言组合，但是却依旧在现实中完全行不通的思考，比如有趣的悖论“无所不能的上帝能否创造出一块儿自己搬不动的石头”，“理发师只给不能给自己理发的人进行理发”。这些悖论就是一种语言推导出来的逻辑，而在维特根斯坦指出那些存在于我们语言中的死路时，这些悖论便有了形式逻辑这一归处。