在人类科技发展的道路上，有很多伟大的科学家，这些科学家对人类科技发展起到了非常重要的作用，如果没有这些科学家做出的贡献，那么人类的科技发展可能要倒退几百年，现代科学认为，人类诞生于200多万年前，当时地球上还生活着很多其它凶猛的生物，猿类生物为了能够长久的发展下去，于是他们选择了群居生活，群居生活不仅仅能够促进彼此之间相互交流的机会，还能够有效的抵抗外来侵略者，科学家经过研究得出，频繁的交流能够使大脑的发育变得越来越快，由于猿类生物长期在一起生活，所以猿类的大脑变得越来越聪明，最终成功进化为人类。

   在人类科技发展的道路上，数学对于人类来说非常重要，数学能够帮助人类实现很多愿望，不过数学也是一个追求极致准确的领域，在这样一个非常严谨的领域当中，一些数学家的理论遭到质疑也是再正常不过的事情，在人类历史上，有很多伟大的数学家终其一生，钻研一个理论，也有很多数学家因为受到外界的质疑，最终失去了宝贵的生命，如果说火的保存为原始人类带来了现实的发展和神秘的色彩，那么数的发现标志着现实和审美的原始进展，我们每一个人从小的时候就开始学习数的概念，不同的东西在计数的意义下能够有相同的量，而这个抽象出来的量被人类称为是数。

   根据科学家的研究得出，数学的历史开始于结绳记事，大约在几万年前，处于原始社会的人类用绳子打结的方式来表示事和数，并且以绳结的方式表示野兽的大小，数的概念就这样慢慢发展起来，在距今5000年前，古埃及人比较早的学习了农业生产，后来在2000多年前，古希腊人继承和发展了数学知识，并将数字发展为一门学科，人类科学上真正的意义研究从古希腊开始，而现代数学史上出现的第一个数学家就是毕达哥拉斯，虽然柏拉图、亚里士多德这些人对后世的影响非常大，但是古希腊最大的成就就是建立了一个比较完美的数学世界，这个数学世界并不像柏拉图的理想国和亚里士多德的形而上学自然观一样。

   它对人类历史产生了非常大的影响，数学给人类带来了理性，它是一种锲而不舍的探索精神，最早把数抽象出来，并把数的地位提高到无与伦比的高度就是古希腊数学家毕达哥拉斯，他也是人类历史上第一个数学家，从此之后，人类研究数学的科学家越来越多，在俄罗斯就有这样一位数学天才罗巴切夫斯基，他所得出的理论在他去世之后才被人类证实，罗巴切夫斯基是俄罗斯著名的数学家，也是非欧几何的最早期发现者之一，罗巴切夫斯基在1807年的时候就以超出常人的智力成功进入了著名的碦山大学。

   在19岁的时候，他就获得了物理数学的硕士学位，在数学领域，最主流的几何方面讨论就是对欧几里得的几何理论研究，其实也就是平面几何和空间几何的研究，欧几里得是历史上非常著名的数学家，他所提出的很多设想，在当时都是不可撼动的真理，这也给后人留下了很多猜想的空间，年前的罗巴切夫斯基也展开了了对平面几何和空间几何的猜测，当时他在研究欧几里得的第五种设想时，突然提出了一个奇怪的疑问：为什么两条平行线一定不会相交呢？这个理论提出之后，很快就遭到了主流数学家的嘲讽，他们认为罗巴切夫斯基的猜测就是一派胡言。

  不过这些质疑并没有影响罗巴切夫斯基的研究，他继续完成了自己的《非欧几何思想》，当时他就如同哥白尼一样，不被认可，但是心中仍然坚持自己的理想和信念，不过现实对于罗巴切夫斯基的打击是非常残酷的，在大家的质疑声中，罗巴切夫斯基不但走下了数学天才的神坛，而且在1856年的时候他离开了世界，享年64岁，在罗巴切夫斯基的心中，一直信奉一个观点：要想将一件事情做得满意，要么就自己去做，要么就自己精通这件事情，保证自己能够对这件事情的人提出精准的、明确的建议。就是因为他和欧几里得的第五大公设，使得他失去了生命。

那么欧几里得的五大公设到底是什么？

   公设1、任意一点到另外一点可以画直线，公设2、一条有限线段可以无限延长，公设3、以任意点为心及任意的距离可以画圆，公设4、凡直角都彼此相等，公设5、若两条直线都与第三条直线相交，并且在同一边的内角只和小于两个直角，则这两条直线在这一边必定相交。在人类数学历史上，有很多数学家想要推翻这五大公设，但是最终都失败了，在此之前，罗巴切夫斯基也和前辈一样，研究欧几里得的五大公设，就在他研究遇到困境的时候，他做出了一个重大的决定，不再继续追寻前人的脚步，他认为，第五公设可能根本不存在，只要能够找到第五公设不可证的答案，那么所有的问题就都解开了。

 不过可惜的是，罗巴切夫斯基有生之年并没有看到自己的理论被人相信，在人类历史上，很多科学家都和罗巴切夫斯基是一样的，哥白尼当年提出日心说，也受到了很多人的质疑和嘲讽，在1543年，哥白尼在临终前发表了《天体运行论》，这个著作被称为是现代天文学的起步点，它开启了哥白尼革命，并推动了科学革命作出了重大的贡献，在哥白尼时代，人们都相信地心说，认为地球是宇宙的中心，太阳和月球都在围绕地球转动，当时哥白尼就发现了地心说的漏洞，在接下来的20年里，他每天坚持观测和测量行星的位置。

  根据多年的观测发现，哥白尼认为地球不可能是行星轨道的中心，而太阳的周年变化并不明显，这意味着地球和太阳的距离始终没有明显的改变，这时候他射线，如果把太阳的位置放在宇宙的中心，那么地球就该围绕太阳转动，之后他便提出了日心说，不过在当时，他的日心说并不被认可，而且他的《天体运行论》也不敢公众于世，直到哥白尼去世之后，《天体运行论》才被世人认可，在17世纪的时候，伽利略和开普勒分别从观测和理论两个层面证明了哥白尼的理论是对的。

  为了纪念哥白尼的成就，月球上最突出的环形山之一被命名为哥白尼环形山，这座直径93千米的环形山最显著的特征是分布在其周围的明亮辐射纹，哥白尼对于后世的影响非常大，如果它不提出日心说，可能人类天文学要退到几百年的时间，这些故事告诉我们，真理总会在历史的长河中浮现出真相，就像罗巴切夫斯基的理论一样，在他死后的12年后，这一理论被意大利数学家贝特拉米所证明，贝特拉米一直都相信罗巴切夫斯基的理论是对的，但是由于当时社会的环境压迫。很多支持罗巴切夫斯基的数学家也无法表达自己的观点，所以他们只能够独自展开对罗巴切夫斯基的理论研究。

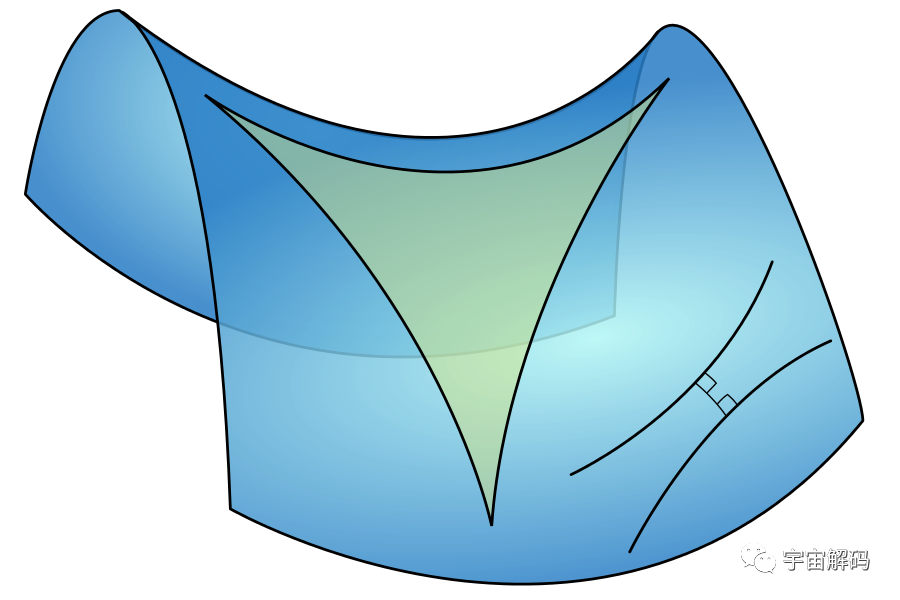
  经过漫长的研究，终于在1868年发表了《关于非欧几里得几何的解释》，并且证明了平行线实际上是可以相交的，他提出欧几里得所提出的平行线无法相交只是在欧几里得平面体系中，而罗巴切夫斯基的平行线相交也要在非欧几何体系中完成，后来碦山大学为了纪念罗巴切夫斯基，在学校内给他建立了一个纪念雕像，提醒众人一定要坚持真理，永不放弃。在我们普通人的认知当中，平行线是不可能相交的，这其实是因为我们的知识局限性造成的，我们上学时所学的平面几何学以欧几里得几何学位框架，其中对平行线的定义就是在二维平面内两条不相交的直线。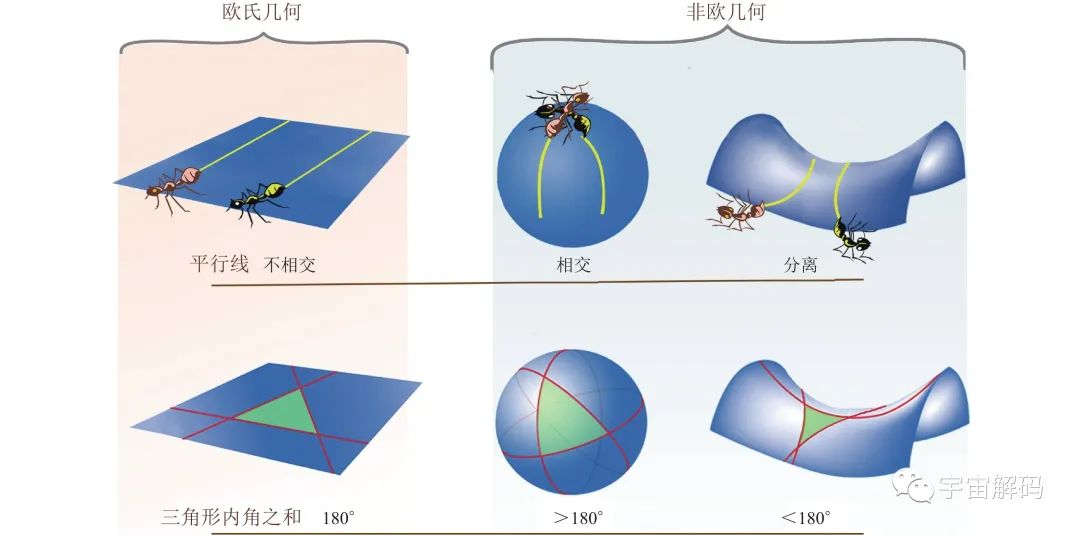

   在欧式几何中，平行线可以无限制的延长，并且永远都不会相交，这种说法也符合人类的直觉尝试，但是如果在一个二维的面上三角形的内角之和可以小于180度，当时也可以大于180度，由于两条直线组成的锐角，向一边作垂线，这个垂线可以和另外一条边不相交，在一个二维面内，过直线外的一点，可以做多条直线与已知直线平行，当然也存在无法做平行线的情况，也就是说在一个二维面上，没有真正的平行线，任何两条直线都有一个共同的交点，在20世纪初的时候，著名的物理学家爱因斯坦在四维空间以及非欧几何的基础上提出了相对论，为人类重新塑造了整个宇宙的时空结构。

   根据爱因斯坦的相对论我们能够知道，平坦的时空只不过是宇宙中小尺度的特例，在大尺度上，不存在所谓的平坦时空，因此非欧几何才是宇宙的本质，因为整个宇宙都存在一定的曲率，虽然我们观测到的宇宙几乎是平坦的，而这只能够说明我们观测到的范围很小，就像我们在地球上看到的地面其实是平面的，但是如果我们站到地球外面，看到的地球其实是一个球状的，而地球本身也是球状的，之所以我们在地面上看到的地球是平面的，是因为我们的观测范围太小了，只能够观测到局部的范围，如果站在整个宇宙的尺度上来说，是不存在绝对的平行线，无限延长的两条线会因为宇宙的曲率而相交。

   伟大的哲学家柏拉图曾经说过一句话：真理可能在少数人一边，在人类历史上，有很多真理提出来的时候都是被质疑的，只有少数人能够坚守，真理从被发现到被大众认可，需要经历漫长的过程，罗巴切夫斯基建立的曲面几何，能够让两条平行的直线，在曲率的改变下相交，这个概念违背了平面几何的定律，但它更加符合宇宙的现实情况，最终被爱因斯坦证实了这一点，每一位科学家的成功都不是偶然的，爱因斯坦能够成为人类历史上最伟大的科学家之一，也是经历了很多磨难，在爱因斯坦之前，所有人都相信牛顿的绝对时空观。

   牛顿认为，时间和空间是一样的，只是一个描述物体运动的几何参量，这是一种空间化的外在时间，时间增加和减少描述了一个物体作为一个点在空间中的位移，并不会涉及和影响物体的内部属性，爱因斯坦出现以后，打破了这个理论，在爱因斯坦的相对论中，阐述了速度和时间的关系，而且还解释了引力和时间的关系，爱因斯坦认为，时间、物质、和空间都是有关系的，现在我们已经证明了时间、空间、物质都是一体的，这一理论颠覆了人类对时间的传统认知，也让科学家对宇宙有了新的认知。

   在人类发展的道路上，有很多曲折，只有那些坚持真理、勇于面对世人的质疑，才能够走到最后，现在人类科学能够有如此高的成就，离不开这些科学家的坚持，目前人类的科技还在不断的进步和发展，人类对世界的认知并不是很全面，在宇宙中依然隐藏着很多我们不知道的奥秘，这些奥秘都在等着人类去探索和研究。