一个有趣的函数问题，还有一种模糊推导圆面积的方法！美国华裔教授专家网 scholarsupdate.hi2net.com

2024-07-02，阅读:116

大家好，我是科学羊。

后面会不定期更新一些数学解题问题，主要面向2类人：

第一类：广大学生，了解有趣的解题技巧；

第二类：感兴趣人群，尤其是像我一样磨一磨生锈的数学大脑；

感谢支持，大家根据兴趣阅读，后期也会讲讲这个栏目进行整合。

Start！

01 一个有趣的函数问题

我们来看一个实际的数学问题，这个数学化简很有意思，题目难度不大，应该是高中水平吧。

请看以下方程，你知道最后f(x)最后可以化简为什么吗？你先自己算算！

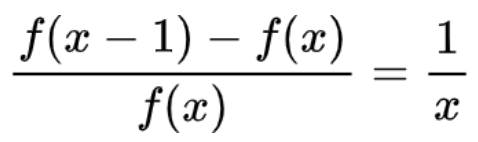
解题过程：

第一步：经过整理和演算，我们会得到 f (x)的一个公式:

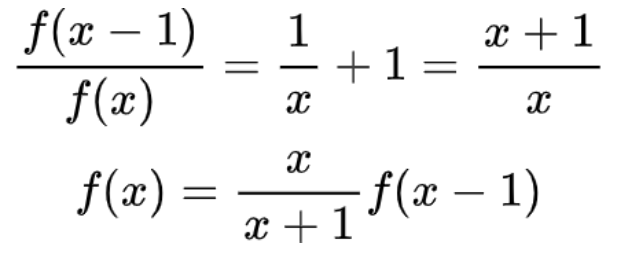
第二步：我们将f(x-1)代入上述公式，就可以得到下面公式：

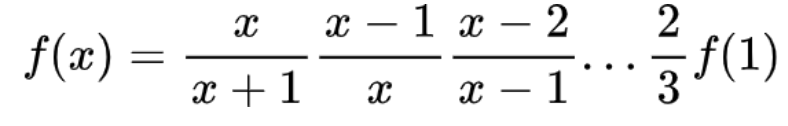
第三步：接下来，分子分母直接化简就可以得到：

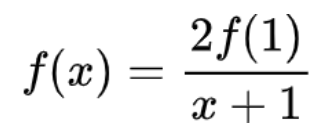
神奇吧，这样一个公式，最后取决于我们对 f (1)的取值！

所以说，你看到的复杂公式最后说不定最后化简为一个很简单的问题。

02 圆面积的一种模糊推导

先问问，你知道多少种求解圆面积的方法吗？

其实有很多种，比如标准公式 πr^2，周长法、积分法、内接正多边形法、蒙特卡洛法、极坐标积分法等......

我们今天看一个另类的方法，用到的知识是：积分 + 泰勒级数 + 正弦定理。

好，先解释下这几个概念：

正弦定律指出，如果 A 和 B 是一个三角形的两条边，而 C 是它们之间的角，那么面积就是:

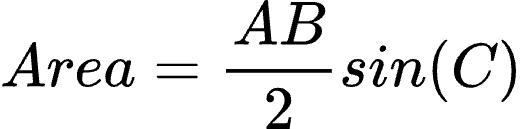
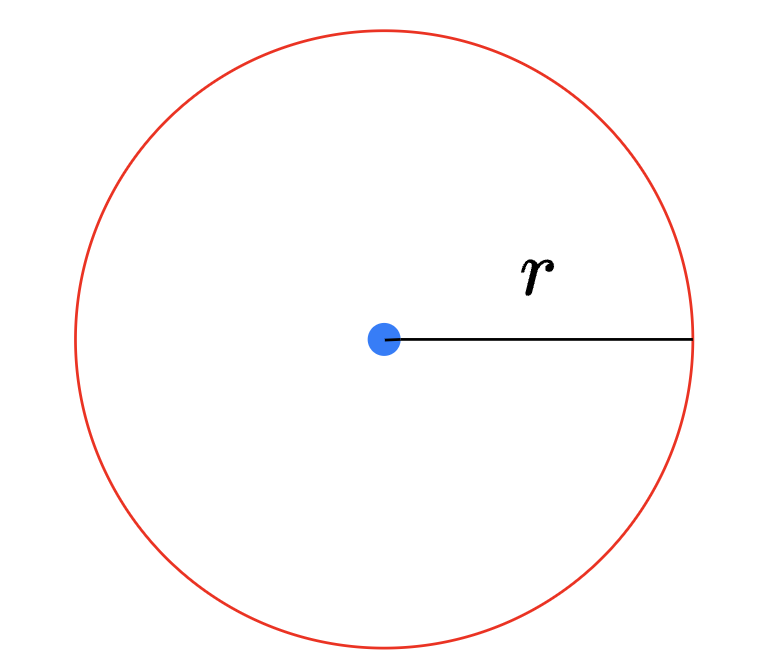
首先，画一个圆

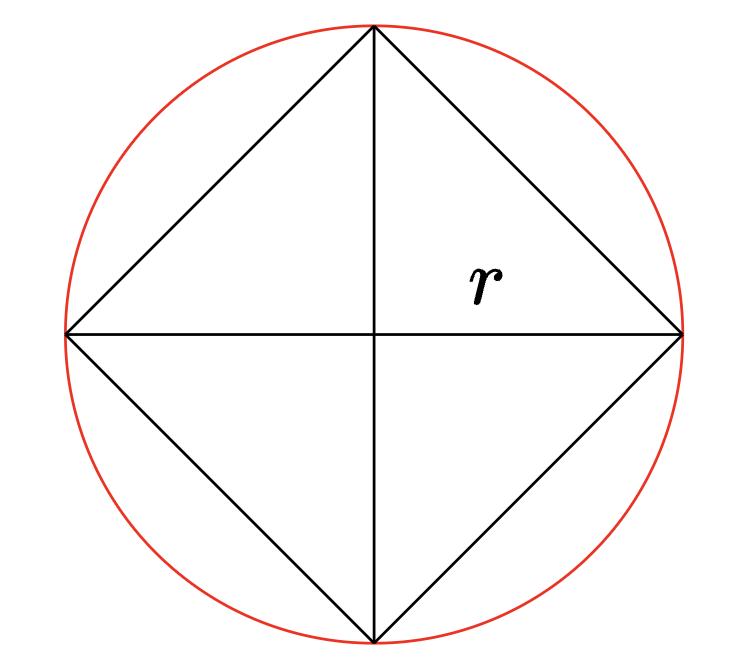
紧接着，我们在园内添加四个接近圆面积的三角形。

对三角形面积求和：

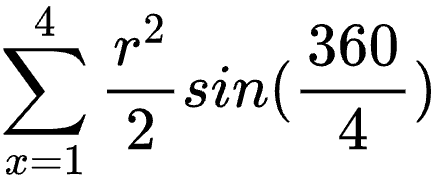
可以看出，实际上所有的三角形都有相同的面积，这取决于它们的角度。

接下来，进行角度转化为弧度的转化，将转化进行积分。

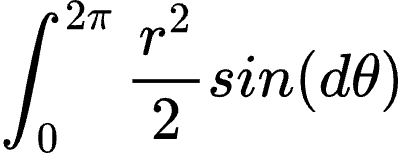
问题是被积函数在函数内部！我们该怎么办？一种方法是用泰勒级数求这个函数。要做到这一点，我们必须知道正弦是:

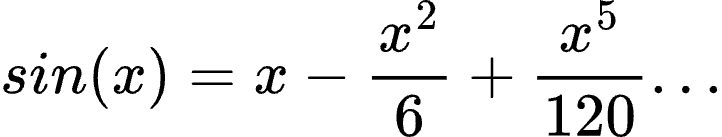
通过将被积函数放入这个函数中，我们得到了无穷小的幂，但在我们的例子中可以忽略这些，因为一旦我们把它们加起来，它们仍然是无穷小的。

所以，我们只需要第一项就是 dθ即可，因此，积分可以为：

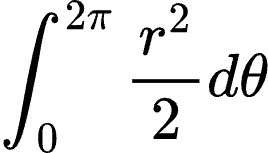
根据积分运算很容易可以得出：

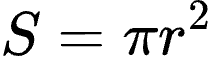
以上！

参考文献：

[1].https://zh.wikipedia.org/wiki/%E6%B3%B0%E5%8B%92%E7%BA%A7%E6%95%B0

[2].https://william-k.medium.com/deriving-the-equation-for-the-area-of-a-circle-28919a51bf29 | William Keens

[3]. 公式 made with Latex

姜鎮英

陳钧铭

郭繁夏

艾红梅

陈岳云